0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖，由本人亲自从底层编写、测试与文章配套的各个经典算法，不依赖于现有库，可以大大加深对算法的理解。

🚀详情：机器学习强基计划(附几十种经典模型源码)

---

1 密度聚类

密度聚类(density-based clustering)的核心原理是通过考察样本分布的紧密程度和可连接性，基于可连接样本不断扩展聚类簇完成聚类过程。

我们用一张图来解释密度聚类的基本概念

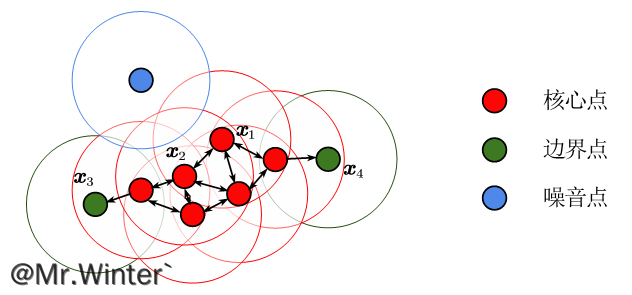
对给定训练集 X = { x 1 , x 2 , ⋯   , x m } X=\left\{ \boldsymbol{x}_1,\boldsymbol{x}_2,\cdots ,\boldsymbol{x}_m \right\} X={x1​,x2​,⋯,xm​}，定义如下基本概念：

• $ϵ$-邻域：样本$\mathbf{x}$的$ϵ$-邻域定义为 N ϵ ( x ) = { x i ∈ X ∣ d i s t ( x i , x ) ⩽ ϵ } N_{\epsilon}\left( \boldsymbol{x} \right) =\left\{ \boldsymbol{x}_i\in X|\mathrm{dist}\left( \boldsymbol{x}_i,\boldsymbol{x} \right) \leqslant \epsilon \right\} Nϵ​(x)={xi​∈X∣dist(xi​,x)⩽ϵ}
• 密度：样本$\mathbf{x}$的密度定义为$p\left(\mathbf{x}\right)=\left|N_{ϵ}\left(\mathbf{x}\right)\right|$；
• 核心点：若$p\left(\mathbf{x}\right)⩾M$则称$\mathbf{x}$是核心点，其中$M$为核心点邻域最小样本数；
• 边界点：若在非核心点$\mathbf{x}$的$ϵ$-邻域中存在核心点，则称$\mathbf{x}$为边界点；
• 噪音点：训练集中除核心点和边界点之外的点为噪音点；
• 密度直达：若样本${\mathbf{x}}_j$位于${\mathbf{x}}_i$的$ϵ$-邻域中且${\mathbf{x}}_i$为核心对象，则称${\mathbf{x}}_j$由${\mathbf{x}}_i$密度直达；
• 密度可达：对于样本${\mathbf{x}}_i$、${\mathbf{x}}_j$，若存在样本序列 { p 1 , p 2 , ⋯   , p n } \left\{ \boldsymbol{p}_1,\boldsymbol{p}_2,\cdots ,\boldsymbol{p}_n \right\} {p1​,p2​,⋯,pn​}，其中${\mathbf{p}}_1={\mathbf{x}}_i$，${\mathbf{p}}_n={\mathbf{x}}_j$且${\mathbf{p}}_{i+1}$由${\mathbf{p}}_i$密度直达，则称${\mathbf{x}}_j$由${\mathbf{x}}_i$密度可达；
• 密度相连：对于样本${\mathbf{x}}_i$、${\mathbf{x}}_j$，若存在${\mathbf{x}}_k$使${\mathbf{x}}_i$与${\mathbf{x}}_j$均由 ${\mathbf{x}}_k$密度可达，则称${\mathbf{x}}_i$与${\mathbf{x}}_j$密度相连;

再看上面这张图，根据定义有：${\mathbf{x}}_2$由${\mathbf{x}}_1$密度直达，${\mathbf{x}}_3$由${\mathbf{x}}_1$密度直达，${\mathbf{x}}_3$与${\mathbf{x}}_4$密度相连。

2 DBSCAN算法

DBSCAN算法是密度聚类的经典算法，定义簇$C$为满足以下性质的非空样本子集：

• 连接性：对$\forall {\mathbf{x}}_i,{\mathbf{x}}_j\in C$，${\mathbf{x}}_i,{\mathbf{x}}_j$密度相连；
• 最大性：对$\forall {\mathbf{x}}_i\in C$，若${\mathbf{x}}_j$由 ${\mathbf{x}}_i$密度可达，则${\mathbf{x}}_j\in C$；

显然，若$\mathbf{x}$为核心点，则由$\mathbf{x}$密度可达的全体样本

V = { x ′ ∈ X ∣ x ′ 由 x 密度可达 } V=\left\{ \boldsymbol{x}'\in X|\boldsymbol{x}'\text{由}\boldsymbol{x}\text{密度可达} \right\} V={x′∈X∣x′由x密度可达}

为一个簇。DBSCAN算法从任意核心点出发，基于密度可达性扩展聚类，完成一簇后再挑选未被选中的核心点重复过程，直至遍历完所有核心点。算法流程如下所示。

3 Python实现

3.1 算法复现

配合算法流程图来看

• 初始化

  # 初始化核心点集合
  core = {i: self.dataSet[i] for i in range(self.m) if len(self.__getEpiNeighbor(self.dataSet[i])) >= self.M}
  # 初始化聚类簇数
  k = 0
  kCluster = {}
  # 初始化未访问样本集合
  flag = np.ones(self.m)
  

• 循环主体

  while len(core) > 0:
      # 生成聚类簇
      k = k + 1
      kCluster[k] = []
      # 随机选取核心点
      o = core.popitem()
      kCluster[k].append(o[1])
      # 初始化队列
      Q = [o]
      # 更新未访问样本集合
      flag[o[0]] = 0
      while len(Q) > 0:
          q = Q.pop(0)
          neighbors = self.__getEpiNeighbor(q[1])
          if len(neighbors) >= self.M:
              for key, value in neighbors.items():
                  if flag[key]:
                      Q.append((key, value))
                      # 设置访问标记
                      flag[key] = 0
                      # 更新簇
                      kCluster[k].append(value)
                      # 更新核心点集
                      if key in core.keys():
                          del core[key]
  

3.2 可视化实验

定义如下可视化函数

def plotGraph(self) -> None:
	kCluster = self.run()
	 for i in kCluster:
	     x = np.array(kCluster[i])[:,0]
	     y = np.array(kCluster[i])[:,1]
	     plt.scatter(x,y)
	 # 绘制噪音向量点的位置
	 xNoise = np.array(self.noise)[:,0]
	 yNoise = np.array(self.noise)[:,1]
	 plt.scatter(xNoise, yNoise, marker='+')
	 plt.title("DBSCAN")
	 plt.show()

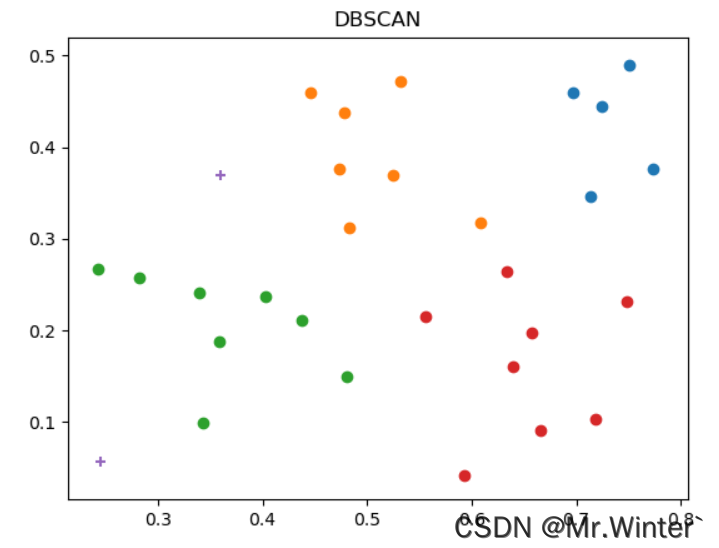
DBSCAN算法的优势是可以自适应地剔除噪音，防止这些异常点影响簇内整体的性质；缺陷是不能手动设置期望聚类的簇数，这点和其他聚类方法不同。

本文完整工程代码联系下方博主名片获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《机器人原理与技术》
• 《机器学习强基计划》
• 《计算机视觉教程》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇