目录
1.排序算法分类
1.直接选择排序
代码展示:
2.直接插入排序
核心思路:
代码展示:
编辑
3.希尔排序
思路分析:
代码展示:
4.归并排序
代码展示:
5.快速排序(挖坑法)
思路分析:
代码展示:
5.快速排序(<算法四>的分区方法)
思路分析:如图所示
代码展示:
代码展示:
1.排序算法分类
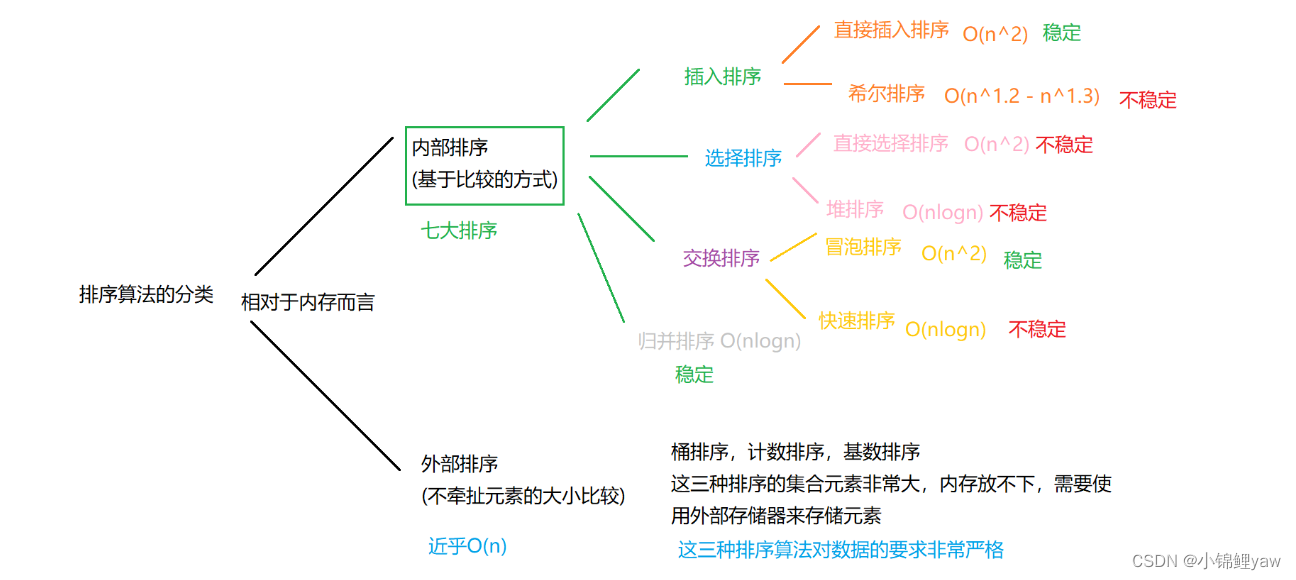
1.直接选择排序
核心思路:每次在无序区间中选择最小值与第一个元素交换,直到整个数组有序(不稳定)
代码展示:
public static void insertSort(int [] arr){
for(int i = 0; i < arr.length; i++){
int min = i;
int j = 0;
for(j = i; j < arr.length; j++){
if(arr[j] < arr[min]){
min = j;
}
}
swap(arr,i,min);
}
}
private static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}2.直接插入排序
在近乎有序的数组上性能非常好
核心思路:
每次从无序区间的第一个位置选取元素,插入到有序区间的合适位置,直至数组有序
代码展示:
public static void selectionSort(int[] arr){
for(int i = 1; i < arr.length; i++){
for(int j = i; j >= 1 && arr[j] < arr[j-1]; j--){
swap(arr,j,j-1);
}
}
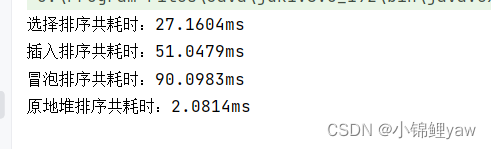
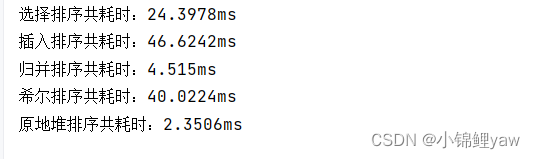
}我们生成随机数组,并运用排序算法对他们分别进行排序,计算并比较插入,选择,冒泡,原地堆排序的排序速度,结果如下:
public static void main(String[] args) {
int n = 10_000;
int[] arr = ArrayUtil.generateRandomArray(n,0,Integer.MAX_VALUE);
int[] arr1 = ArrayUtil.arrCopy(arr);
int[] arr2 = ArrayUtil.arrCopy(arr);
int[] arr3 = ArrayUtil.arrCopy(arr);
int[] arr4 = ArrayUtil.arrCopy(arr);
//
long start = System.nanoTime();
selectionSort(arr);
long end = System.nanoTime();
if(isSorted(arr)){
System.out.println("选择排序共耗时:"+(end - start)/1000000.0+"ms");
}
start = System.nanoTime();
insertSort(arr1);
end = System.nanoTime();
if(isSorted(arr1)){
System.out.println("插入排序共耗时:"+(end - start)/1000000.0+"ms");
}
start = System.nanoTime();
bubbleSort(arr2);
end = System.nanoTime();
if(isSorted(arr2)){
System.out.println("冒泡排序共耗时:"+(end - start)/1000000.0+"ms");
}
start = System.nanoTime();
heapSort(arr3);
end = System.nanoTime();
if(isSorted(arr3)){
System.out.println("原地堆排序共耗时:"+(end - start)/1000000.0+"ms");
}
}可以看到在这四种排序算法中,原地堆排序最快,冒泡排序最慢
3.希尔排序
思路分析:
有人发现插入排序在数组内元素近乎有序的时候性能极好,所以发明了希尔排序
将原数组分成若干个子数组,先将子数组内部调整为有序,当最终分组长度为1时,整个数组接近有序,最后再来一次插入排序(此时性能最好)即可~
代码展示:
public static void shellSort(int[] arr){
//先分组
int gap = arr.length >> 1;
if(gap > 1){
insertSort(arr,gap);
gap >>= 1;
}
//此时整体进行一次插入排序
insertSort(arr,1);
}
private static void insertSort(int[] arr,int gap){
//按照gap进行插入排序
for(int i = gap; i < arr.length; i++){
for(int j = i; j - gap >= 0 && arr[j] < arr[j - gap]; j -= gap){
swap(arr,j,j-gap);
}
}
}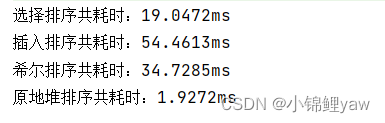
结果可以看到,希尔排序比插入排序的速度要快,在这里选择比希尔排序要快是java编译器的原因,具体我也不清楚,等我在学一段时间来解答吧~
4.归并排序

1.不断地将原数组一分为二,直到拆分后的子数组只剩下一个元素
2.不断地将两个连续的有序子数组合并为一个大的有序数组,直到合并后的数组长度等于元数组的长度,即排序完成~
代码展示:
优化一:当子数组内元素小于64个元素时,使用直接插入排序会更高效
优化二:当两个子数组连接已经有序的时候,可以不用在进行排序
//归并排序
public static void mergeSort(int[] arr){
mergeSortInternal(arr,0,arr.length - 1);
}
private static void mergeSortInternal(int[] arr, int l, int r) {
//优化一
if(r - l <= 64){
insertionSort(arr,l,r);
return;
}
int mid = l + ((r - l) >> 1);
mergeSortInternal(arr,l,mid);
mergeSortInternal(arr,mid + 1,r);
//优化二
if(arr[mid] > arr[mid + 1]){
merge(arr,l,mid,r);
}
}
private static void insertionSort(int[] arr, int l, int r) {
for(int i = l + 1; i <= r; i++) {
for (int j = i; j > l && arr[j] < arr[j-1]; j--) {
swap(arr,j,j - 1);
}
}
}
private static void merge(int[] arr, int l, int mid, int r) {
//创建一个和原数组长度一样的新数组
int [] aux = new int[r - l + 1];
System.arraycopy(arr,l,aux,0,r - l + 1);
int i = l;
int j = mid + 1;
for (int k = l; k <= r; k++) {
if(i > mid){
arr[k] = aux[j - l];
j++;
}else if(j > r){
arr[k] = aux[i - l];
i++;
}else if(aux[i - l] <= aux[j - l]){
arr[k] = aux[i - l];
i++;
}else {
arr[k] = aux[j - l];
j++;
}
}
}
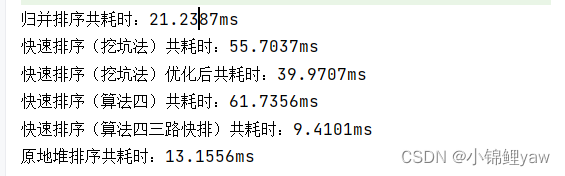
结果可以看到,当数据量在10000时,归并排序比选择,插入,希尔排序都要快,
5.快速排序(挖坑法)
思路分析:
每次从无序数组中选取一个元素作为分区点(pivot),将原集合中所有小于pivo的元素放在该元素的左侧,将所有大于pivot的元素放在该元素的右侧,继续在左侧和右侧区间重复此过程,直到整个数组有序
代码展示:
优化一:当子数组内元素小于64个元素时,使用直接插入排序会更高效
public static void quickSortHole(int[] arr) {
quickSortHoleInternal(arr,0,arr.length - 1);
}
private static void quickSortHoleInternal(int[] arr, int l, int r) {
if(r - l <= 64){
insertionSort(arr,l,r);
return;
}
int p = partitionByHole(arr,l,r);
quickSortHoleInternal(arr,l,p - 1);
quickSortHoleInternal(arr,p + 1,r);
}
private static int partitionByHole(int[] arr, int l, int r) {
int pivot = arr[l];
int i = l;
int j = r;
while (i < j){
while (i < j && arr[j] >= pivot) {
j--;
}
arr[i] = arr[j];
while (i < j && arr[i] <= pivot) {
i++;
}
arr[j] = arr[i];
}
arr[i] = pivot;
return i;
}结果可以看到,在100 0000数量级下,快排比堆排快了接近一倍的速度

但是呢,挖坑这种方法下的堆排有一个弊端,就是在近乎有序的数组上,时间复杂度会下降为O(n),出现这种情况是我主要原因是我们每次选择pivot的时候选择的都是最左边,所以我们只需要每次在无序数组的下标中随机选择一个与最左边进行交换,这样就可以避免在近乎有序的数组上快排性能下降的问题
代码展示:
public static void quickSortHole1(int[] arr) {
quickSortHoleInternal(arr,0,arr.length - 1);
}
private static void quickSortHoleInternal1(int[] arr, int l, int r) {
if(r - l <= 64){
insertionSort(arr,l,r);
return;
}
int p = partitionByHole(arr,l,r);
// 继续在两个子区间上进行快速排序
quickSortHoleInternal(arr,l,p - 1);
quickSortHoleInternal(arr,p + 1,r);
}
private static int partitionByHole1(int[] arr, int l, int r) {
Random random = new Random();
int indexRandom = random.nextInt();
swap(arr,indexRandom,l);
int pivot = arr[l];
int i = l;
int j = r;
while (i < j){
while (i < j && arr[j] >= pivot) {
j--;
}
arr[i] = arr[j];
while (i < j && arr[i] <= pivot) {
i++;
}
arr[j] = arr[i];
}
arr[i] = pivot;
return i;
}
可以看到,在10000数据量的数组中,优化后的快排性能提升了不少
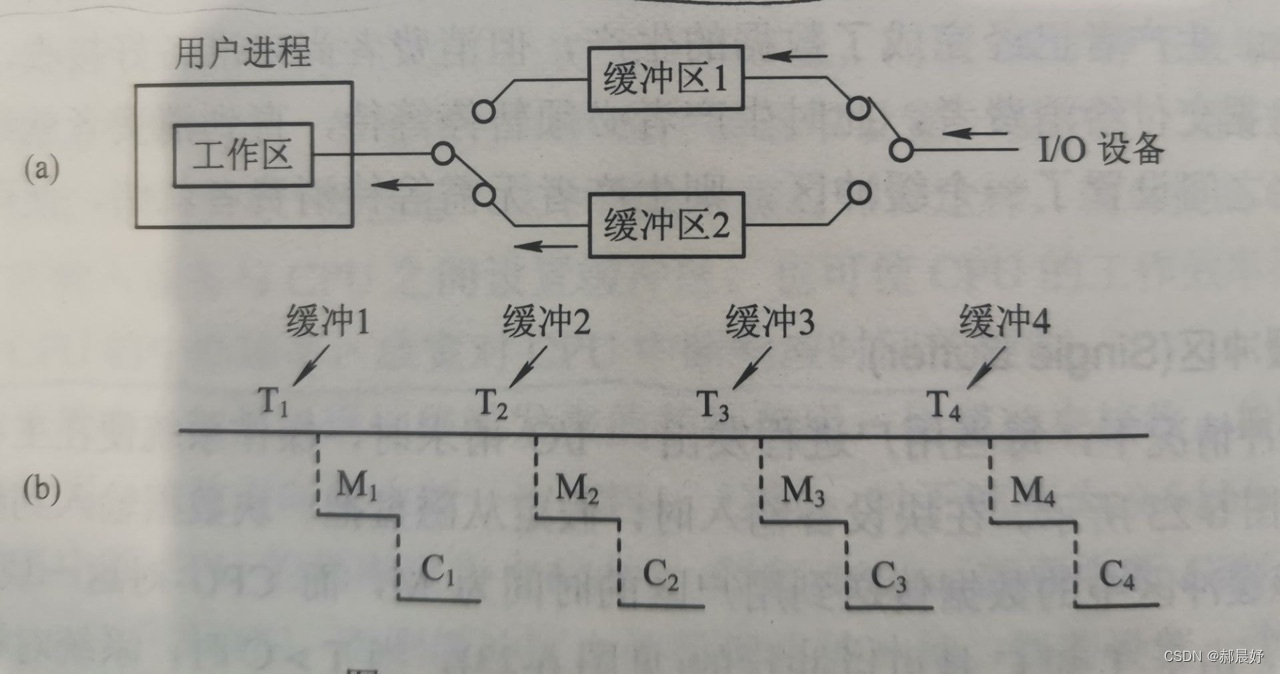
5.快速排序(<算法四>的分区方法)
思路分析:如图所示

代码展示:
public static void quickSortFour(int[] arr){
quickSortFourInternal(arr,0, arr.length - 1);
}
private static void quickSortFourInternal(int [] arr, int l, int r){
if(r - l <= 64) {
insertionSort(arr,l,r);
return;
}
int p = partitionByFour(arr,l,r);
quickSortFourInternal(arr,l,p - 1);
quickSortFourInternal(arr,p + 1,r);
}
private static int partitionByFour(int[] arr, int l, int r) {
int indexRandom = ThreadLocalRandom.current().nextInt(l,r);
swap(arr,l,indexRandom);
int pivot = arr[l];
int j = l;
for (int i = l + 1; i <= r; i++) {
if(arr[i] < pivot) {
swap(arr,i,j+1);
j++;
}
}
swap(arr,l,j);
return j;
}
上面的快排虽说经过优化对近乎有序的数组进行排序会性能下降的问题解决了,可在当数组中·有大量重复元素时,快排性能依然会下降
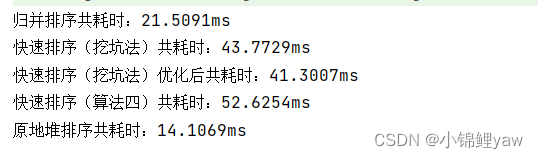
可以看到在100000数据量的情况下,原地堆排比快排序块了将近三四倍
所以我们提出了新的方法(三路快排)
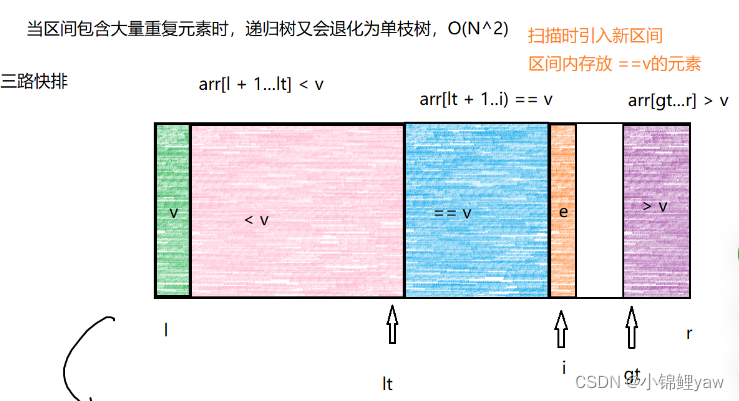
代码展示:
public static void quicSortByThree(int[] arr) {
quicSortByThreeInternal(arr,0,arr.length - 1);
}
private static void quicSortByThreeInternal(int[] arr, int l, int r) {
if(r - l <= 64) {
insertionSort(arr,l,r);
return;
}
int [] res = partitionByThree(arr,l,r);
quicSortByThreeInternal(arr,l,res[0] - 1);
quicSortByThreeInternal(arr,res[1] + 1,r);
}
private static int[] partitionByThree(int[] arr, int l, int r) {
int indexRandom = ThreadLocalRandom.current().nextInt(l,r);
swap(arr,indexRandom,l);
int pivot = arr[l];
int lt = l;
int gt = r + 1;
for(int i = l + 1; i < gt; i++) {
if(arr[i] < pivot) {
swap(arr,lt + 1, i);
lt++;
}else if(arr[i] > pivot) {
swap(arr,gt - 1, i);
gt--;
i--;
}
}
swap(arr,l,lt);
return new int[]{lt, gt - 1};
}
当数组中有大量重复元素时,可以看见三路快排的速度是最快的