13444 - 求出e的值
时间限制 : 1 秒
内存限制 : 128 MB
利用公式e=1+1/!1+1/2!+1/3!+...+1/n!,求e的值,要求保留小数点后10位。
输入
输入只有一行,该行包含一个整数n(2≤n≤15),表示计算e时累加到1/n!。
输出
输出只有一行,该行包含计算出来的e的值,要求打印小数点后10位。
样例
输入
10
输出
2.7182818011
答案:
#include<iostream>
using namespace std;
int main() {
int n = 0;
long long mul = 1;
cin >> n;
double e = 1;
for (int i = 1; i <= n; i++) {
mul *= i;
e += 1.0/mul;
}
cout.precision(10);
cout.flags(cout.fixed);
cout << e << endl;
return 0;
}分析:这道题刚开始我是编写的时候,那个mul定义为int。但是int最大范围是21亿,但是13的阶乘就已经到了62亿多。所以int的范围是接受不了的。而long一般也是4字节,一般范围和int一样。所以一般 long long 来定义。
是否通过:
13462 - 跳一跳(建议二刷)
时间限制 : 1 秒
内存限制 : 128 MB
近来,跳一跳这款小游戏风靡全国,受到不少玩家的喜爱。 简化后的跳一跳规则如下:玩家每次从当前方块跳到下一个方块,如果没有跳到下一个方块上则游戏结束。 如果跳到了方块上,但没有跳到方块的中心则获得 1 分;跳到方块中心时,若上一次的得分为 1 分或这是本局游戏的第一次跳跃则此次得分为 2 分,否则此次得分比上一次得分多两分(即连续跳到方块中心时,总得分将 +2,+4,+6,+8…)。 现在给出一个人跳一跳的全过程,请你求出他本局游戏的得分(按照题目描述的规则)。
输入
输入包含多个数字,用空格分隔,每个数字都是 1,2,0 之一,1 表示此次跳跃跳到了方块上但是没有跳到中心,2 表示此次跳跃跳到了方块上并且跳到了方块中心,0 表示此次跳跃没有跳到方块上(此时游戏结束)。
对于所有评测用例,输入的数字不超过 30 个,保证 0 正好出现一次且为最后一个数字。
输出
输出一个整数,为本局游戏的得分(在本题的规则下)。
样例
输入
1 1 2 2 2 1 1 2 2 0
输出
22
答案:
#include<iostream>
using namespace std;
int main() {
//isFirst用来判定是否是第一次跳到正中心
//flag用来判断是否连续跳到正中心
int n,isFirst=1,flag=0;
int last = 0,sum=0;//last为上次跳的距离
while (true){
cin >> n;
if (n == 1) {
isFirst = 0;
last = 1;
sum += last;
flag = 0;
}
else if (n == 2) {
if (isFirst == 1) {//第一次跳到正中心
isFirst = 0;//若第一次跳到正中心,将isFirst设置为0,即这一局不会再发生第二个第一次跳到正中心
last = 2;
sum += last;
flag = 1;
}
else if (flag == 1) {
last += 2;
sum += last;
}
else if (flag == 0) {//连续跳到正中心中断,即累计积分又得从2开始
last = 2;
sum += last;
flag = 1;//虽然中断,但是从这一步起,将连续标志设为1
}
}
else {
break;
}
}
cout << sum << endl;
return 0;
}分析:这道题逻辑看似简单,但实现还是有困难的。要判定第一次是否跳到正中心,而且还要判断是否连续跳到正中心。
21201 - 成绩排序
时间限制 : 1 秒
内存限制 : 128 MB
输入10个学生的成绩,并将10个学生的成绩按由大到小的顺序排序。
输入
10整数表示10个学生的成绩(整数与整数间使用空格隔开)
输出
10个按由大到小排好序的成绩
样例
输入
20 30 40 50 60 70 80 90 91 95
输出
95 91 90 80 70 60 50 40 30 20
答案:
#include<iostream>
#include<algorithm>
using namespace std;
bool cmp(int a, int b) {
return a > b;
}
int main() {
int a[10];
for (int i = 0; i < 10; i++) {
cin >> a[i];
}
sort(a, a + 10,cmp);
for (int i = 0; i < 10; i++) {
cout << a[i] << ' ';
}
return 0;
}分析:其实要单说排序不难,这道题放在这里就是掌握C++的快速排序库函数sort(形参a,形参b )
sort( )函数可以有两个参数,也可以有三个参数,当为两个参数时,默认是升序排序。有三个参数时,要根据第三个参数才能决定是升序还是降序。本题cmp()函数返回的是a>b,这是降序。如果是a<b,这是升序。形参a和形参b是待排序数据的地址范围。
另外在这里给出C语言的快速排序,就当复习一下:
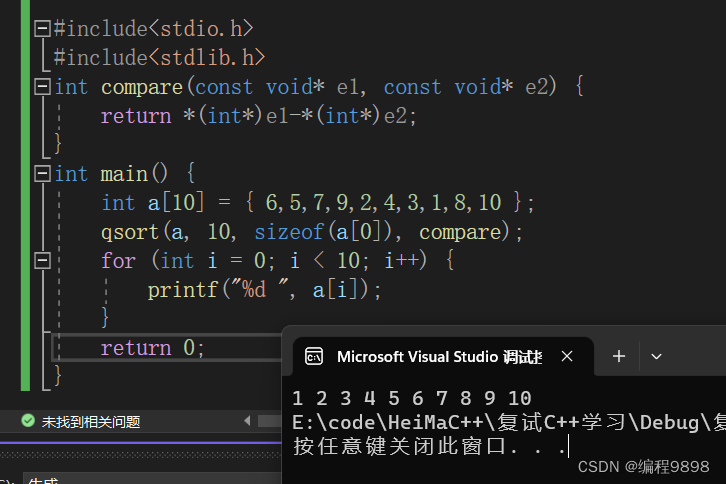
21203 - 整数重组
时间限制 : 1 秒
内存限制 : 128 MB
任意给定一个整数,把它重新组成一个最大数和一个最小数,求出两数的差。
例如:3721,可以重组成:7321和1237,两数之差为7321-1237=6084
输入
x(整数 1 <= x <= 10,000,000)
输出
最大数和最小数的差
样例
输入
102
输出
198
答案:
#include<iostream>
using namespace std;
int main() {
int n, max=0, min=0;//max为重组的最大值,min为重组的最小值
int a[9] = { 0 };//用来记录这个数各个位数有多少个,用来计算最大值
int b[9] = { 0 };//用来记录这个数各个位数有多少个,用来计算最小值
cin >> n;
int r = 0,count1=0,mul=1;
while (n) {
r = n % 10;
n /= 10;
count1++;//统计改数字有几位
a[r]++;
b[r]++;
}
//重组最大值
int count2 = count1;
for (int i = 9; i > 0; i--) {
while (a[i] > 0) {//为什么要循环,是因为当出现重复的数字后所以要循环
for (int j = 1; j < count1; j++) {
mul *= 10;
}
max += i * mul;
a[i]--;
mul = 1;
count1--;
}
}
//重组最小值
mul = 1;
for (int i = 0; i <= 9; i++) {
if (b[i] > 0 && i == 0) {
count2 -= a[i];
}
while (b[i] > 0 && i !=0 ) {
for (int j = 1; j < count2; j++) {
mul *= 10;
}
min += i*mul;
count2--;
mul = 1;
b[i]--;
}
}
cout << max - min << endl;
return 0;
}分析:这道题是不简单。当然看你用什么方法,若用一维数组来解决的话其实没那么复杂,我用两个一维数组的目的是引入哈希存储思想。因为后面会有类似的题。大家可用一个一维数组来解决这个题。
是否通过:
21301 - 约瑟夫问题(经典问题!二刷)
时间限制 : 1 秒
内存限制 : 128 MB
n个人(n<=100)围成一圈,从第一个人开始报数,数到m的人出列,再由下一个人重新从1开始报数,数到m的人再出圈,……依次类推,直到所有的人都出圈,请输出依次出圈人的编号。
输入
n m(1≤m,n≤100)
输出
出圈的编号
样例
输入
10 3
输出
3 6 9 2 7 1 8 5 10 4
答案:
#include<iostream>
using namespace std;
#define MAX 101
int main() {
int n, m;//n个人,数到m
int a[MAX];
cin >> n >> m;
int count = 0;//记录数数,从1数到m后又从1开始计数
int sum = n;//每退出一个人,直到最后一个人退出
int k = 0;
for (int i = 1; i <= n; i++) {
a[i] = i;//注意下标从1开始
}
while(true){
k++;//数数下标
if (k > n) {
k = k % n;
}
if (a[k]) {//只有当前位置没有退出时,数数才加1
count++;
}
if (count == m) {//每次数到m
if (a[k]) {
cout << a[k] << ' ';
sum--;
if (sum == 0) {
break;
}
a[k] = 0;//退出这个位置的人,设置为0表示退出
}
count = 0;//每次退出一个人又要重新开始报数
}
}
return 0;
}分析:这个题难度还是很大的,当数数等于m时,得重新开始数。其次,当下标为k大于当前人数时,又得通过取模返回到下标为1的位置。其次,当访问到已经退出的下标时,数数不算。因为退出的人不能再数数。最后还得通过一个变量sum来记录人是否全部退出。一系列条件加起来,这个题难度就很大了。在做这个题时最好现在草稿纸上自己演算一遍理清思路。
是否通过: