【二叉树扩展学习】💯💯💯
- 1.【二叉树的创建】
- 2.【二叉树的销毁】
- 3.【二叉树的前序遍历】
- 4.【二叉树的中序遍历】
- 5.【二叉树的后序遍历】
- 6.【二叉树的层序遍历】
- 7.【二叉树的高度】
- 8.【二叉树结点的个数】
- 9.【第K层二叉树的结点个数】
- 10.【二叉树查找值为x的结点】
- 11.【单值二叉树】
- 12.【检查两颗树是否相同】
- 13.【对称二叉树】
- 14.【另一颗树的子树】
- 15.【判断一棵树是否是完全二叉树】
1.【二叉树的创建】
通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
> 基本思想:
<利用前序遍历的方式来创建二叉树>
1.当遇到#则要返回,相当于遇到空返回。
2.当遇到非#,那就要为它创建节点,将它塞到节点里。
3.创建好节点后就要为左右孩子创建节点。
注意点:在递归里如果有要进行自增或自减的变量,不能传变量给函数,而是应该传改变量的指针过去。比如下面的&i
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
typedef char STDataType;
typedef struct BinaryTreeroot
{
struct BinaryTreeroot* left;
struct BinaryTreeroot* right;
STDataType data;
}BTroot;
BTroot* CreatBinaryTree(char*a,int *pi)//创建二叉树
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
//如果不是#那就是字母,如果是字母那就要为它分配节点
BTroot* root = (BTroot*)malloc(sizeof(BTroot));
if (root == NULL)
{
perror("malloc");
}
//将字母塞到节点里
root->data = a[*pi];
(*pi)++;
//创建完节点后就要为左孩子和右孩子创建节点
root->left=CreatBinaryTree(a, pi);
root->right= CreatBinaryTree(a, pi);
return root;
}
2.【二叉树的销毁】
通过后序遍历对二叉树"ABD##E#H##CF##G##"销毁
> 基本思想:
<利用后序遍历思想进行二叉树销毁>
1.销毁二叉树需要将所以节点销毁
2.前序遍历销毁根节点后,左右孩子无法找回,不方便销毁左右孩子
3.后序遍历先销毁左孩子,再销毁右孩子,最后销毁根节点。
void DestroyBinaryTree(BTroot* root)//销毁二叉树
{
if (root == NULL)
{
return;
}
//销毁二叉树 先销毁左子树-右子树-根
DestroyBinaryTree(root->left);
DestroyBinaryTree(root->right);
free(root);
}
3.【二叉树的前序遍历】
> 基本思想:
1.一旦遇到空节点就要往后返回2.前序遍历顺序:先访问根节点—再访问左子树—再访问右子树
void BinaryTreePrevOrder(BTroot* root)//二叉树前序遍历
{
if (root == NULL)
{
printf("#");
return;
}
printf("%c", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
递归展开图:
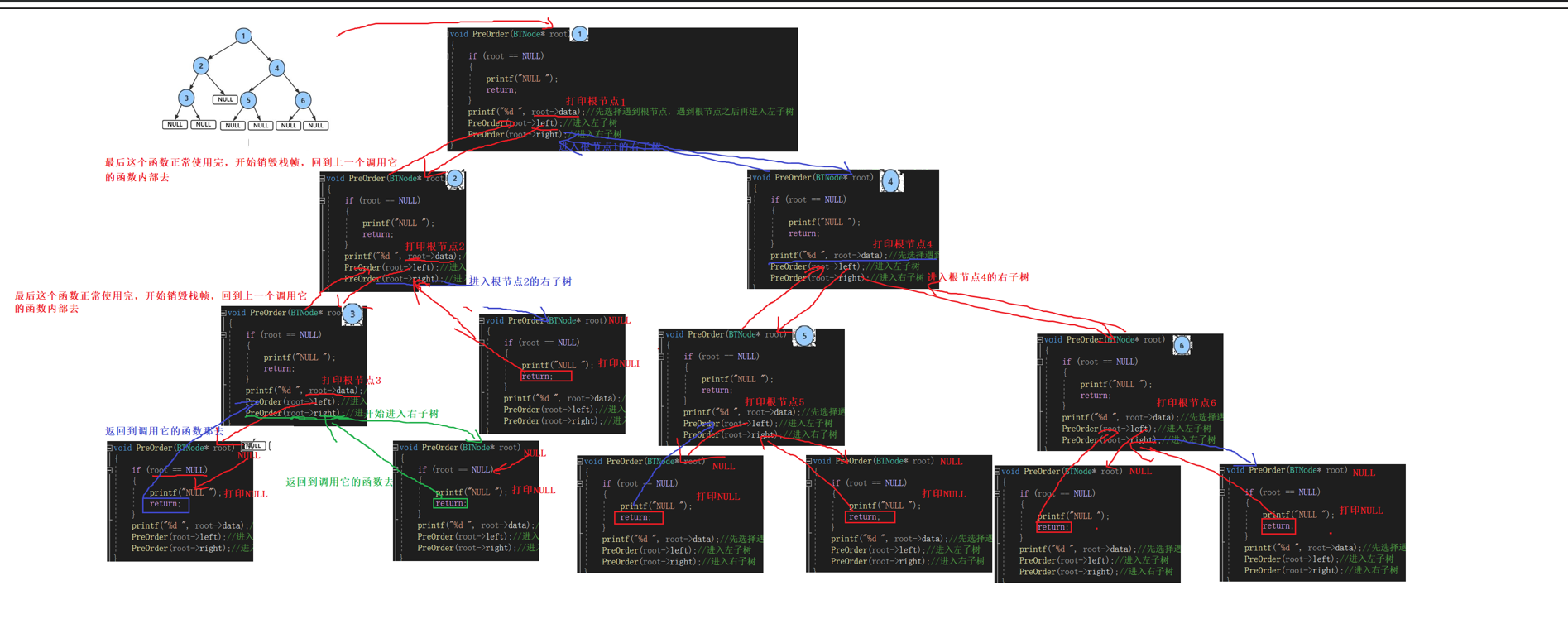
4.【二叉树的中序遍历】
> 基本思想:
1.一旦遇到空节点就要往后返回2.中序遍历顺序:先访问左子树—再访问根节点—再访问右子树
void BinaryTreeInOrder(BTroot* root)//二叉树中序遍历
{
if (root == NULL)
{
printf("#");
return;
}
BinaryTreePrevOrder(root->left);
printf("%c", root->data);
BinaryTreePrevOrder(root->right);
}
递归展开图:
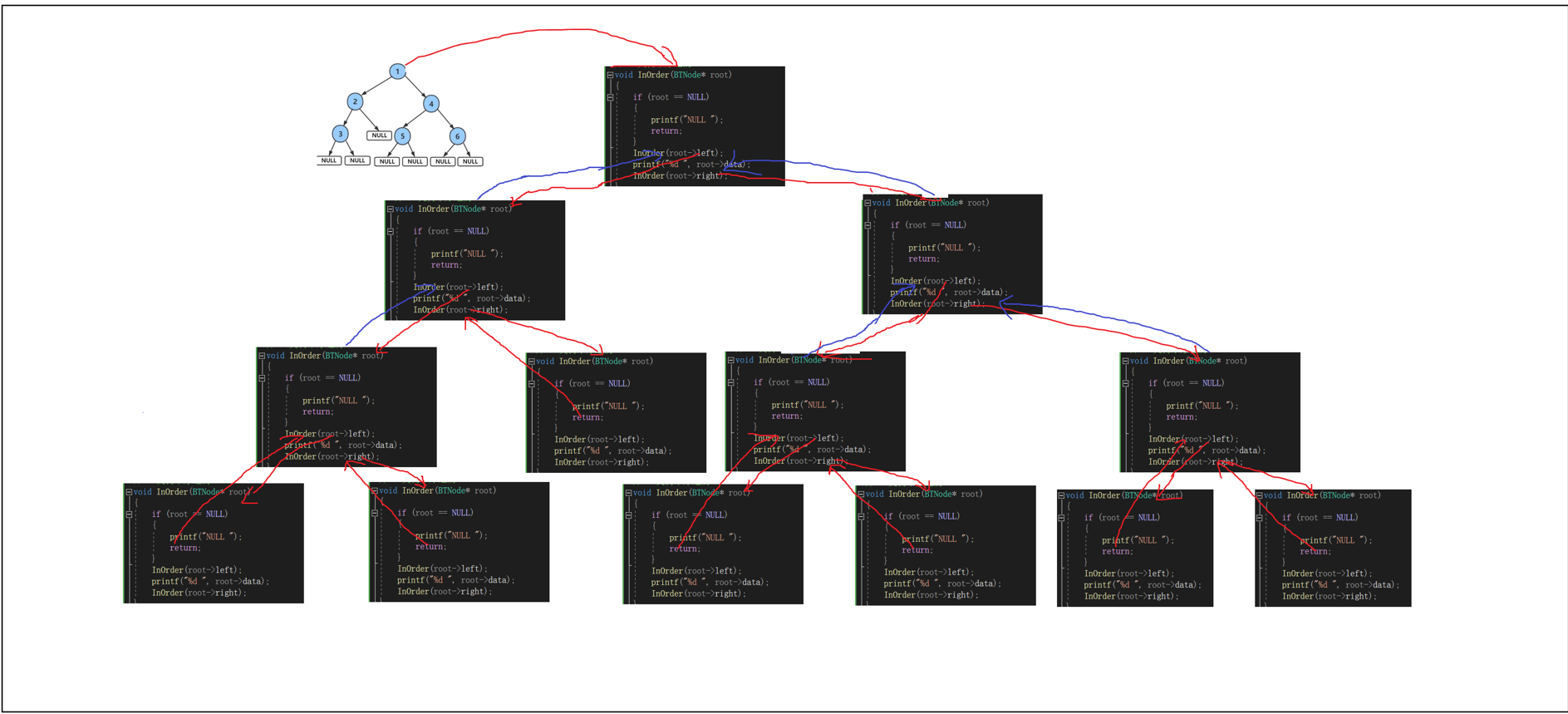
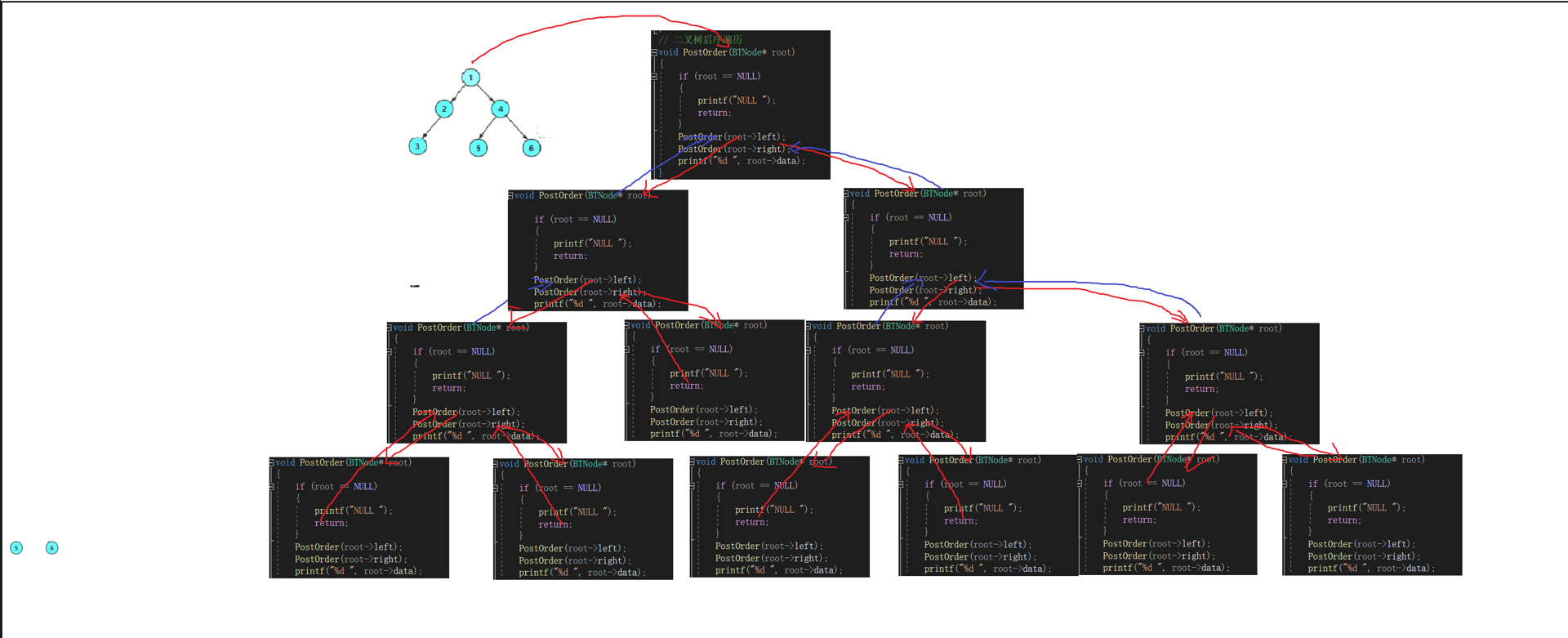
5.【二叉树的后序遍历】
> 基本思想:
1.一旦遇到空节点就要往后返回2.后序遍历顺序:先访问左子树—再访问右子树—再访问根节点
void BinaryTreePostOrder(BTroot* root)//二叉树后序遍历
{
if (root == NULL)
{
printf("#");
return;
}
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
printf("%c", root->data);
}
递归展开图:
6.【二叉树的层序遍历】
通过利用栈辅助来帮助二叉树遍历
> 基本思想:
1.首先需将根节点入栈。
2.根据栈是否为空来对栈里元素进行出栈
3.每次出栈元素前,先保存下这个元素。
4.每次将元素出栈后,需要将出栈元素的孩子入栈
void LevOlder(BTNode* root)//层序遍历--
{
Queue q;//定义一个队列
QueueInit(&q);//初始化队列
//首先将根 指针插入到队列里去
if (root)
{
QueuePush(&q, root);
}
//再出上一层带入下一层
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);//保存一下这个要出队列的指向结点的指针
QueuePop(&q);
printf("%d ", front->data);
//出完后再将它的孩子指针带入进来
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestroy(&q);
}
7.【二叉树的高度】
利用分治递归子问题思想
> 基本思想:
1.求二叉树高度,其实就是求左右子树中较高的子树的高度
2.我们想象根节点是一个校长,它位高权重,并不想下去一个一个数。
3.而左右节点看作院长,校长让左院长去找左子树中最高的。让右院长去找右子树中最高的。
4.而左院长也让它的下面左系主任去数左系最高的,右主任数右系最高……
5.最后院长得到左右院最高的,然后再一比,就可以得到左右院中较高的了。
注意:
1.为什么最后要加1呢?想一想左右子树的高度最后还要加上根节点的这个高度才是最后的高度。
2.注意这里必须要保存左右子树中的最高者,不然递归起来很麻烦。
int BinaryTreeHeight(BTroot* root)//二叉树的高度
{
if (root == NULL)
return 0;
int leftheight = BinaryTreeHeight(root->left);
int rightheight= BinaryTreeHeight(root->right);
return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}
递归展开图:
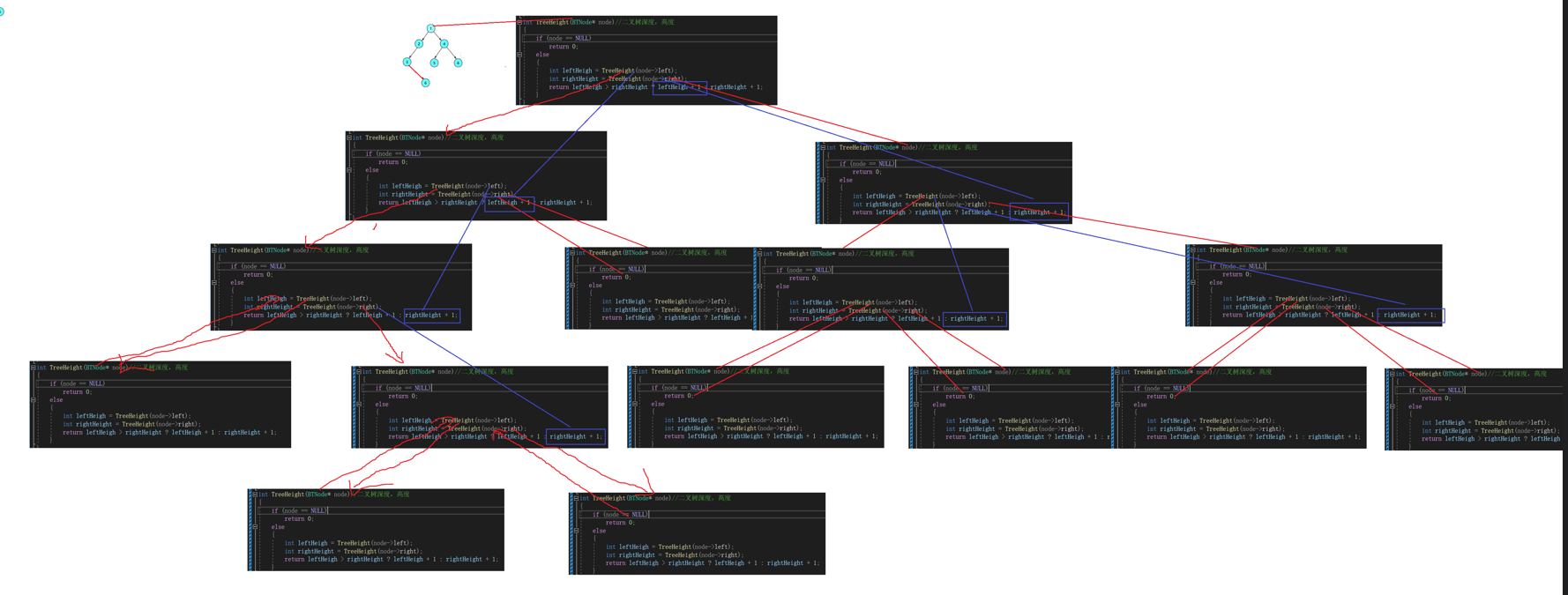
8.【二叉树结点的个数】
利用分治递归子问题思想
> 基本思想:
1.将根节点可成院长,院长要数全校的人数,它肯定不会自己一个一个数的
2.将任务分给分院长,分院长再将任务分给系主任,系主任再将任务分给班长,班长开始数人数
3.班长数完人数后就开始返回到系主任那报告,报告给主任的数字是原数据上再加1,因为自己还没算进去。
4.系主任得到数据后也返回到分院长那,将数据报告给院长,这个数据是原数据再+1,因为系主任也要把自己算进去。
5.最后校长就得到左右院的人数了。
int BinaryTreeSize(BTroot* root)//二叉树节点的个数
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
递归展开图:
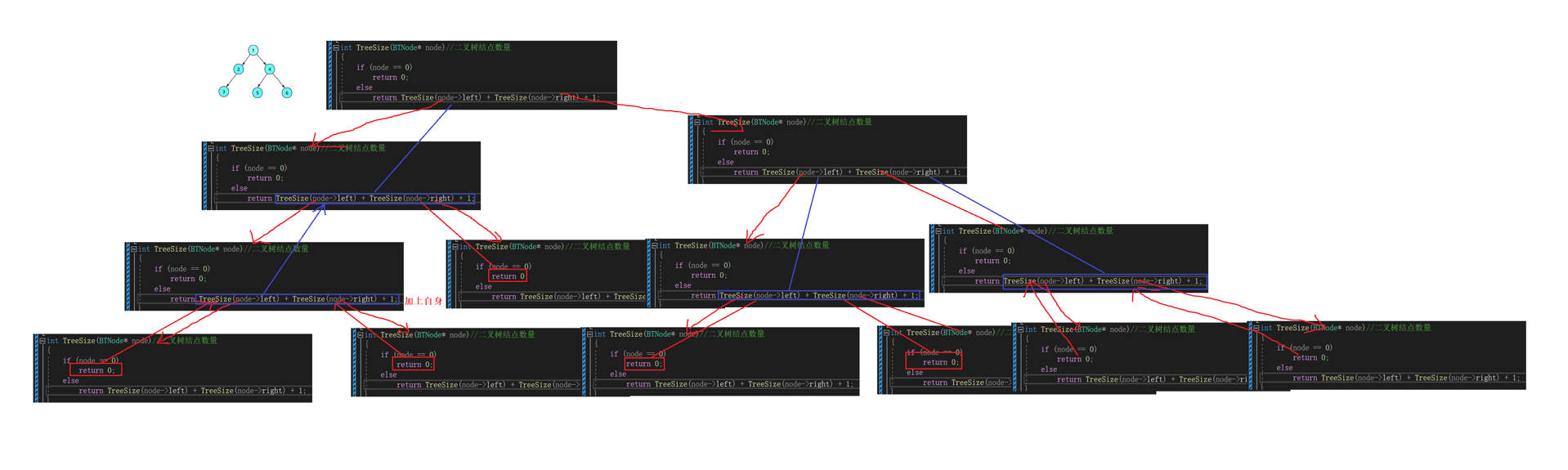
9.【第K层二叉树的结点个数】
利用分治递归子问题思想
> 基本思想:
1.第K层二叉树的节点个数就是左右子树中第K层节点个数相加
2.而根的第K层,相对于左子树来说是第K-1层,相对于左子树的左子树来说是第K-2层……
3.就比如根的第3层相当于左子树的第2层,相当于左子树的左子树第1层。
4.而我们就需要相当于第一层时节点的个数。
int BinaryTreeLevelKSize(BTroot* root,int k)//二叉树第K层节点的个数
{
if (root == NULL)
return 0;
if (k == 1)//当k=1时,就是根的第K层,只不过对于子树来说是第1层
return 1;
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
递归展开图:
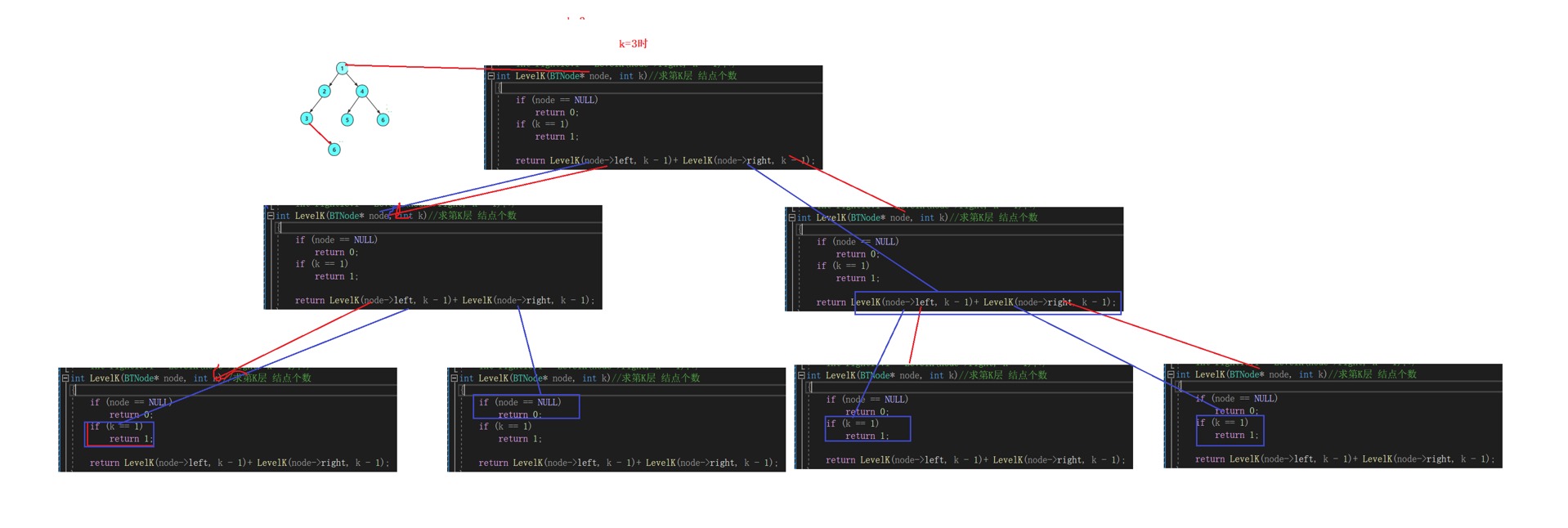
10.【二叉树查找值为x的结点】
利用分治递归子问题思想
> 基本思想:
1.当找到该节点后就将该节点返回。
2.先到左子树中找一遍,如果有就返回。
3.再到右子树中找一遍,如果有就返回。
4.最后如果左右子树都没有就返回空。
BTroot* BinaryTreeFind(BTroot* root, STDataType x)//二叉树查找值为x的节点
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTroot* leftx = BinaryTreeFind(root->left, x);
if (leftx->data == x)
return leftx;
BTroot*rightx= BinaryTreeFind(root->right, x);
if (rightx->data == x)
return rightx;
return NULL;
}
11.【单值二叉树】
利用分治递归子问题思想
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
> 基本思想:
1.我们不用一个一个遍历比较
2.将根节点看作校长,校长要全校做核酸,比较,我们不用校长和全校人比较。
3.只要校长和两个院长一起做核酸。一旦出现阳性就表明不同
4.分院长再和2个系主任做核酸,一旦出现阳性表明不同。
5.系主任和班长做核……班长和同学做核酸……。
6.当遇到空时,没有违法规则,返回true.
7.当一旦出现不同的则全校显示的都为阳性。
注意:在访问左子树之前要确保左子树是不为空的。
bool isUnivalTree(BTroot* root)
{
if(root==NULL)
{
return true;
}
if(root->left&&root->val!=root->left->val)//首先要确保左子树还存在,才可以访问。校长和左院长做核酸
{
return false;//一旦出现阳性,则全校混合都为阳性
}
if(root->right&&root->val!=root->right->val)//确保右子树存在,校长和右院长做核酸
{
return false;//一旦出现阳性,则全校混合都为阳性
}
return isUnivalTree(root->left)&&isUnivalTree(root->right);//最后如果都没有阳性则表明全校都为阴性都相同。
}
12.【检查两颗树是否相同】
利用分治递归子问题思想
如果两个树在结构上相同,并且具有相同的值,则表明它们是相同的。
> 基本思想:
1.首先要确定结构上要相同
2.当为空时应该两个树都为空,当在同一个位置一棵树为空,另一个树不为空,那么这两个树一定不相同。
3.然后确定两个树应该具备相同的值
4.当在相同的位置,两个树的值不相同时,那么这两个树一定不相同。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p==NULL&&q==NULL)//如果遇到空,那么应该同时都遇到空这样才是符合结构相同的
{
return true;
}
if(p==NULL&&q!=NULL||q==NULL&&p!=NULL)
{
return false;//如果在相同的位置一棵树为空,另一棵树不为空,那么肯定不相同。
}
if(p->val!=q->val)//如果两棵树的值不相同那么两棵树肯定不相同。
{
return false;
}
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);//左子树要和左子树相同,右子树要和右子树相同,当没有结构问题,值问题最后两棵树就相同。
}
13.【对称二叉树】
如何判断一棵树是否对称呢?
利用分治递归子问题思想
> 基本思想:
1.找到可以递归的点
2.如何判断一棵树是否为对称二叉树?
当根节点为空时,是对称,当根节点不为空时,要满足的条件是左右子树对称。
3.如何判断左树与右树是否对称呢?
当左树的左子树等于右树的右子树时。【结构和值必须都相同】
当左树的右子树等于右树的左子树时。【结构和值必须都相同】
4.所以递归点就找到了:
一颗树如何对称?<= = =>左右树对称<= = =>左树左孩子等于右树右孩子&&左树右孩子等于右树左孩子。
一颗树对称取决于所有的左树左孩子等于右树右孩子&&左树右孩子等于右树左孩子。
iscomp函数是用来判断左树与右树是否对称的。
bool iscomp(struct TreeNode* leftroot,struct TreeNode* rightroot)
{
if(leftroot==NULL&&rightroot==NULL)//左树和右树都为空时,对称
return true;
if(leftroot==NULL||rightroot==NULL||leftroot->val!=rightroot->val)//当左树或者右树其中有一个为空,另一个不为空时,或者左树值不等于右树值都不是对称
return false;
return iscomp(leftroot->left,rightroot->right)&&iscomp(leftroot->right,rightroot->left);//对左树的左子树和右树的右子树进行递归判断 对左树的右子树和右树的左子树进行判断,两个都为正,才是对称。一个出现假则不对称。
}
bool isSymmetric(struct TreeNode* root)
{
if(root==NULL)//如果根为空,则对称
return true;
//如果根不为空,就判断左树和右树是否对称
return iscomp(root->left,root->right);
}
14.【另一颗树的子树】
利用分治递归子问题思想
看是否另一颗树是否可以看成自己的子树
如果可以那么就是子树,如果不可以那就不是。
> 基本思想:
1.可以利用两个树是否相同的思路。
2.将树1的左子树和子树比较,将树1的右子树和子树比较。
3.如果子树相同返回true
4.如果树1为空那肯定不会有子树了。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p==NULL&&q==NULL)
{
return true;
}
if(p==NULL&&q!=NULL||q==NULL&&p!=NULL)
{
return false;
}
if(p->val!=q->val)
{
return false;
}
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if(root==NULL)
return false;
if(isSameTree(root,subRoot))
{
return true;//如果树1的子树和子树相同则返回true
}
return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);//左右子树中只要有一个子树满足条件即可。
}
15.【判断一棵树是否是完全二叉树】
利用满二叉树性质判断:非空节点连续
> 基本思想:
1.根据满二叉树性质:非空节点是连续出现的。
2.当一旦出现了空节点那么后面就不可以再出现非空节点
3.空节点后面一旦出现非空节点,那么该树一定不是完全二叉树。
4.层序遍历二叉树来判断空节点后面是否还会出现非空节点。
bool BTreeCompele(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)//将根节点插入到队列中
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);//出队列中的元素
if (front == NULL)
{
break;
}
//如果front不为空,就将它的孩子插入到队列中去,空节点也插入进去,不需要讨论
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//break 跳出来需要判断是否后面还会出现非空节点
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);//出队列中的元素
if (front)//如果队列中出的节点不为空节点
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}