文章目录
- 内存单元的理解
- 结构体中内存对齐的规则
- 为什么会存在内存对齐
一、内存单元的理解
首先先要介绍一下C语言中一些常见的存储单元
bit 存放一个二进制位
Byte 1Byte = 8 bit
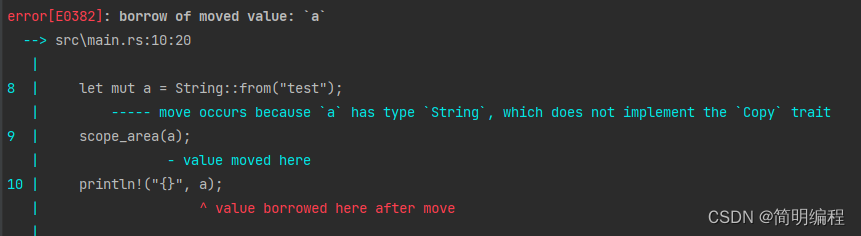
KB 1KB = 1024 Byte
MB 1MB = 1024 KB
GB 1GB = 1024 MB
TB 1TB = 1024 GB
PB 1PB = 1024 TB
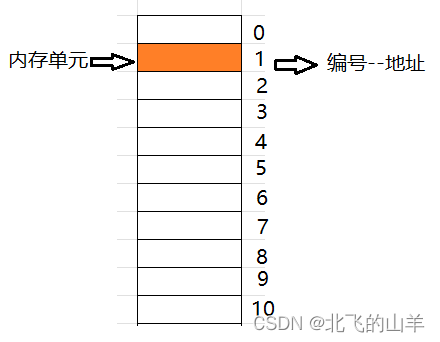
一个内存单元的大小占一个字节(Byte)。内存单元是一片连续的空间,对其的编号也是连续的。
如下图所示:
接下来,我们来探讨一下地址编号是如何产生的:
其实,在我们的计算机上,存在着这样的一种物理的电线,叫地址线。地址线一旦通电以后,就会产生电信号,形成高电平或者低电平。高低电平信号可以转换成数字信号,对应的就是1或者0。32位机器上有32根地址线,32根地址线通电后32个电平信号就可以转换成对应的32位的01二进制序列。

从上图可以看到,32根地址线产生的地址编号总共就有个。假设32个0序列用来管理上上图中0编号所指向的内存单元,31个0序列和最后的一个1所组成的序列用来管理1号所指向的内存单元,以此类推。这样,物理电线上所产生的电信号转换成的数字信号就可以被用来管理内存单元。也就是说,32位机器下就可以管理就可以管理
个Byte大小的内存,也就是4GB大小的内存。
二、结构体中内存对齐的规则
1. 第一个成员在与结构体偏移量为0的地址处。
2. 其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。注意:对齐数 = 编译器默认的一个对齐数 与 该成员大小的较小值。(VS中默认的对齐数为8)
3. 结构体总大小为:最大对齐数(所有变量类型最大者与默认对齐参数取最小)的整数倍。
4. 如果嵌套了结构体的情况,嵌套的结构体对齐到自己的最大对齐数的整数倍处,结构体的整体大小就是所有最大对齐数(含嵌套结构体的对齐数)的整数倍。
下面我将对这四条规则进行解释:
1.第一个成员在与结构体偏移量为0的地址处。
首先我们应理解什么是偏移量,见下图:
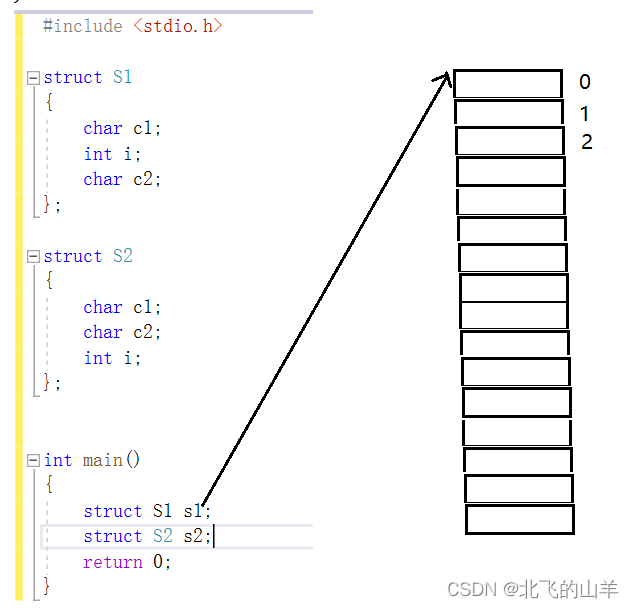
假定由结构体S1创建出的s1在内存中的起始位置是图中所指向的横线,那么其下面的第一个存储单元的偏移量就是0,s1的第一个成员就从偏移量为0这个存储单元开始存储。
2.其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。注意:对齐数 = 编译器默认的一个对齐数 与 该成员大小的较小值。(VS中默认的对齐数为8)
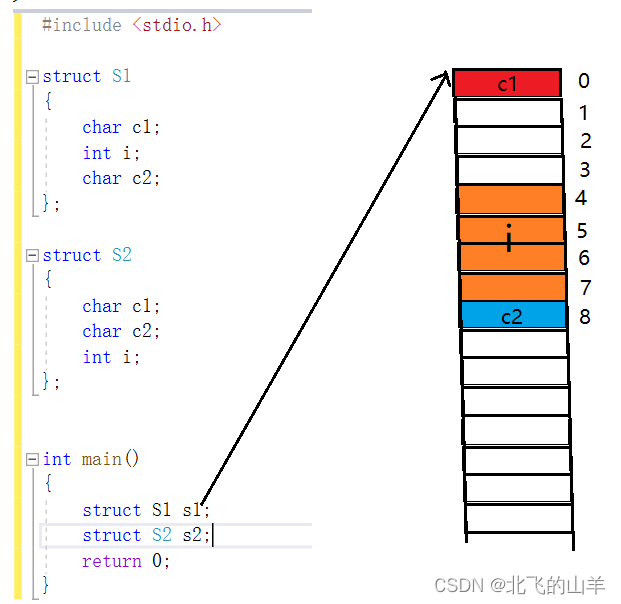
如图所示:c1是s1的第一个成员,存放在偏移量为0处,s1的第二个成员i的类型为int,大小为4个Byte,因为4小于8,所以i这个变量应该从偏移量为4的倍数处开始存放,存放4个Byte。最后c2的大小为1,从偏移量为1的倍数处开始存放,即紧跟着i变量存储即可。
3.结构体总大小为:最大对齐数(所有变量类型最大者与默认对齐参数取最小)的整数倍。
以上图中的S1来举例,其三个成员的类型分别为char,int,char,类型大小分别为1,4,1,所以所有变量类型最大者即为int,其大小为4Byte,小于VS的默认对齐参数(8Byte),所以最大对齐数为4,即创建出来的结构体变量s1的大小必须为4的倍数。从上图可知,此时s1已经占用了9个Byte,但还需向内存申请3个Byte大小的空间,构成12个Byte大小的空间,即s1的大小占12个Byte。
4. 如果嵌套了结构体的情况,嵌套的结构体对齐到自己的最大对齐数的整数倍处,结构体的整体大小就是所有最大对齐数(含嵌套结构体的对齐数)的整数倍。
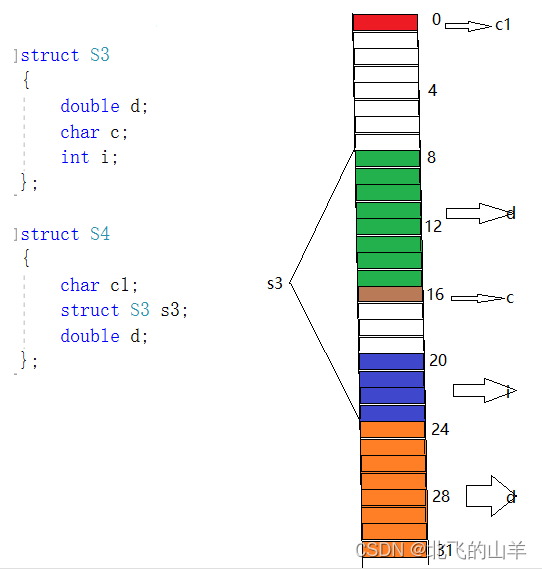
由上图以及两个结构体成员可知,S3的最大默认对齐数是8,所以s3的第一个成员要从偏移量为8的位置开始存放,其他存放规则与上面三条规则相同,最终S4的大小占32个Byte。
三、为什么会存在内存对齐
1. 平台原因(移植原因):
不是所有的硬件平台都能访问任意地址上的任意数据的;某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。
2. 性能原因:
数据结构(尤其是栈)应该尽可能地在自然边界上对齐。
原因在于,为了访问未对齐的内存,处理器需要作两次内存访问;而对齐的内存访问仅需要一次访问。
为什么未对齐的内存,处理器需要作两次内存访问呢?见下图:
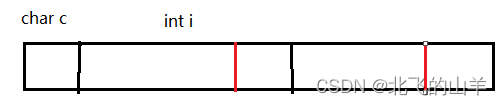
在32位机器下,一次可以访问4个Byte,假设不采用内存对齐的方式,int类型的变量前有一个char类型的变量c,那么处理器要完全访问到i,第一次需要先访问c变量以及i变量的前三个字节,第二次再访问i的最后一个字节,这样就需要访问两次才能完全访问完i。
总体来说:
结构体的内存对齐是拿空间来换取时间的做法。
那在设计结构体的时候,我们既要满足对齐,又要节省空间,我们应该:
让占用空间小的成员尽量集中在一起。