【树】你真的会二叉树了嘛? --二叉树LeetCode专题Ⅳ

news2025/1/25 9:05:54

Halo，这里是Ppeua。平时主要更新C语言，C++，数据结构算法......感兴趣就关注我吧！你定不会失望。

🌈个人主页：主页链接

🌈算法专栏：专栏链接

我会一直往里填充内容哒！

🌈LeetCode专栏：专栏链接

目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目，也会当天做完发出

🌈代码仓库：Gitee链接

🌈点击关注=收获更多优质内容🌈

题目:111. 二叉树的最小深度

题解:

代码实现:

题目:700. 二叉搜索树中的搜索

题解:

代码实现:

题目:701. 二叉搜索树中的插入操作

题解:

代码实现:

题目:450. 删除二叉搜索树中的节点

题解:

代码实现:

完结撒花：

人生苦短，我爱算法!(哭

本章依然是二叉树的刷题忘记的朋友们可以去看看我的二叉树专题

题目:111. 二叉树的最小深度

题解:

这题和之前做过的,寻找二叉树的最大深度类似.

寻找最大深度是返回最大的节点深度+1(本层节点数)

寻找最小深度就是返回最小的深度再+1(本层节点数)

但是!!!

有个问题,若左子树为空因为取min则其会直接返回0,但我们深度最低都是一.所以我们需要加一个判断是否为空,若为空则返回另一个枝.

若都不为空则按上面的逻辑进行操作即可.

代码实现:

class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==NULL)return 0;
        int left=minDepth(root->left);
        int right=minDepth(root->right);
        if(left==0)return right+1;
        if(right==0)return left+1;
        return left>right?right+1:left+1;
    }
};

题目:700. 二叉搜索树中的搜索

题解:

在开始先,我们先了解一下什么是

BST(Binary Search Tree)二叉搜索树:有点类似堆对数据的操作,其左子树的值小于根的值小于右子树的值

换一种说法就是任何一个右子树的节点都大于左子树的节点,且根节点的值介于二者之间

所以其有左小右大的特点.

所以有了这个特点后在搜索树中找值就很简单啦!

若其大于目标值,就说明要往小的方向找.也就是left

若其小于目标值,就说明要往大的方向找,也就是right

代码实现:

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root==NULL)return NULL;
        if(root->val==val)return root;
        TreeNode*tmp1=NULL;
        TreeNode*tmp2=NULL;
        if(root->val>val)
            tmp1=searchBST(root->left, val);
        if(root->val<val)
            tmp2=searchBST(root->right, val);
        if(tmp1!=NULL)return tmp1;
        return tmp2;
    }
};

题目:701. 二叉搜索树中的插入操作

题解:

插入与上面的搜索有些许类似,为了满足BST的数据结构.需要找到一个合适的地方进行插入.

如果root.->val大于插入值,就说明这个值得放在其的左边

如果root.->val小于插入值,就说明这个值得放在其的右边

当root==NULL的时候,就说明找到了插入的位置,则创建一个新的节点,放入值,并且返回.

代码实现:

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root==NULL)return new TreeNode(val);
        if(root->val<val)root->right=insertIntoBST(root->right,val);
        if(root->val>val)root->left=insertIntoBST(root->left,val);
        return root;
    }
};

题目:450. 删除二叉搜索树中的节点

题解:

如果是一颗普通的二叉树,想要删除其左/右节点,则让其root->left/root->right=NULL即可也就是递归返回值为NULL(在不考虑内存泄漏的情况下)

那如果是一颗BST,那就要保证删除时,其性质不变,仍然是一颗BST;

这里仍然需要find,但因为前面说过了,就不过多赘述.

那么分几种情况来讨论

1.删除的节点为一个叶子节点:那么直接返回NULL即可.这样并不会影响其性质

2.删除的节点为一个仅有左子树/右子树的节点:则直接返回其左子树/右子树即可

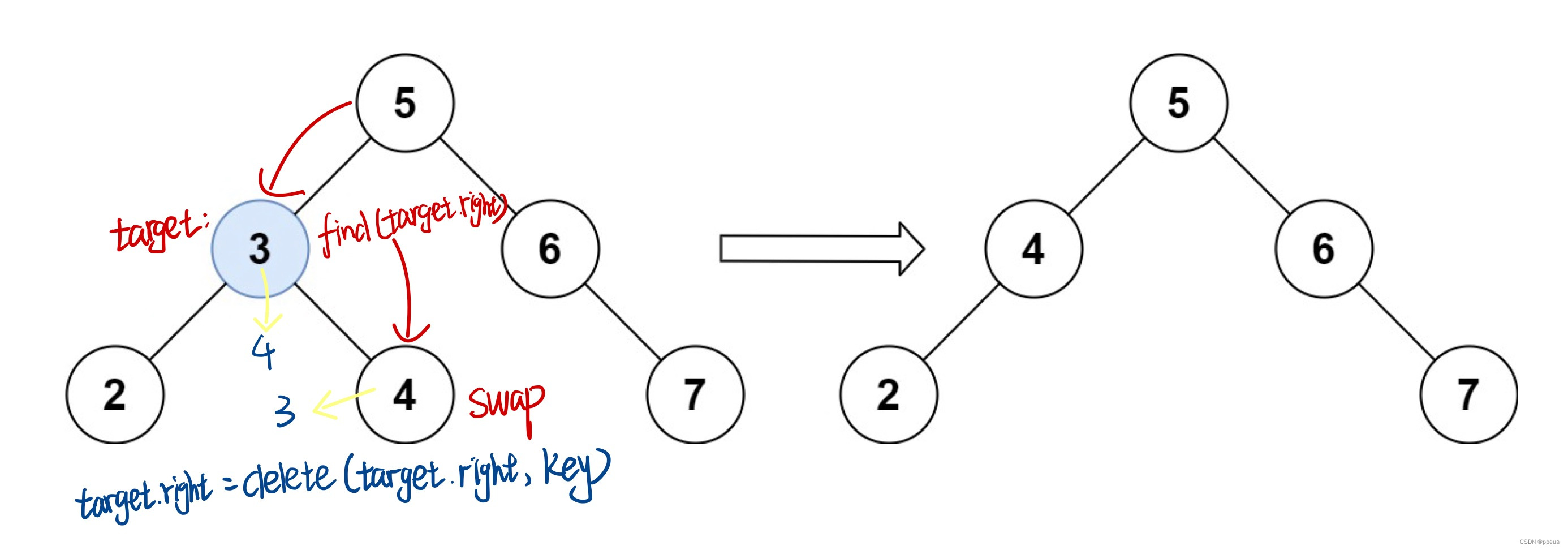
3.删除的节点为一个仅有左子树/右子树的节点:

则需要找到其右子树中最小的值(也就是右子树中的左叶子)

其值会比所有左子树的节点大,也会比所有右子树节点小.

之后将其值赋值给刚刚找到的目标节点,现在要做的就是去目标节点的右子树中删除刚刚的叶子节点,也就变成了情况1

代码实现:

class Solution {
public:
    TreeNode*find(TreeNode* root)
    {
        if(!root->left)return root;

        return find(root->left);
    }
    TreeNode* deleteNode(TreeNode* root, int key) {
        //find
        if(root==NULL)return NULL;
        if(root->val==key)
        {
            //delete
            if(!root->left&&!root->right)
            {
                return NULL;
            }
            else if(!root->left)
            {
                return root->right;
            }
            else if(!root->right)
                return root->left;
            TreeNode *tmp=find(root->right);
            root->val=tmp->val;
            root->right=deleteNode(root->right,tmp->val);
        }
        else if(root->val<key)root->right=deleteNode(root->right, key);
        else if(root->val>key)root->left=deleteNode(root->left, key);
        return root;
    }
};