我们的目标:
1、了解线性结构的特点 掌握顺序表的定义、查找、插入和删除。
2、掌握链表的定义、创建、查找、插入和删除。
3、能够从时间和空间复杂度的角度比较两种存储结构的不同特点及其适用场合。(持续更新)
前言
本章节内容主要介绍线性表的链式表示和实现,即链表的使用。
继续上一篇内容:http://t.csdn.cn/KwKsg
三、链表
我们都知道,线性表的链式存储结构的特点是在逻辑上相邻的数据元素在物理上不一定相邻。
上一篇我们讲到了单链表,所以接下来来介绍循环链表。
1.1 循环链表
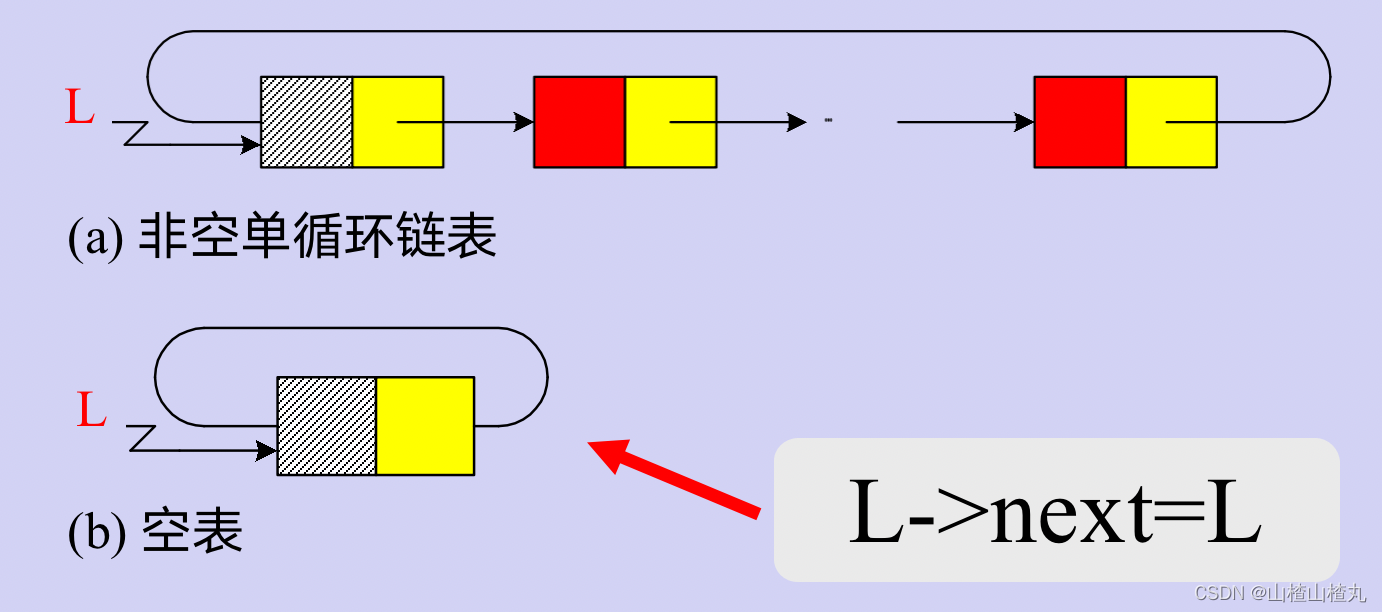
循环链表是另一种形式的链式存储结构。和单链表不同的是,它最后不是NULL,而是L(通俗来讲因为循环没有尽头)。
类似地,还有非空单循环链表和空表。如图所示:
这说明了从循环链表中的任何一个结点的位置都可以找到其他所有结点,而单链表做不到;
并且循环链表中没有明显的尾端——>如何避免死循环?
我们知道循环条件是
//单链表
p!=NULL
p->next!=NULL
//循环链表
p!=L
p->next!=L
进而说明对循环链表,有时不给出头指针,而给出尾指针可以更方便的找到第一个和最后一个结点。
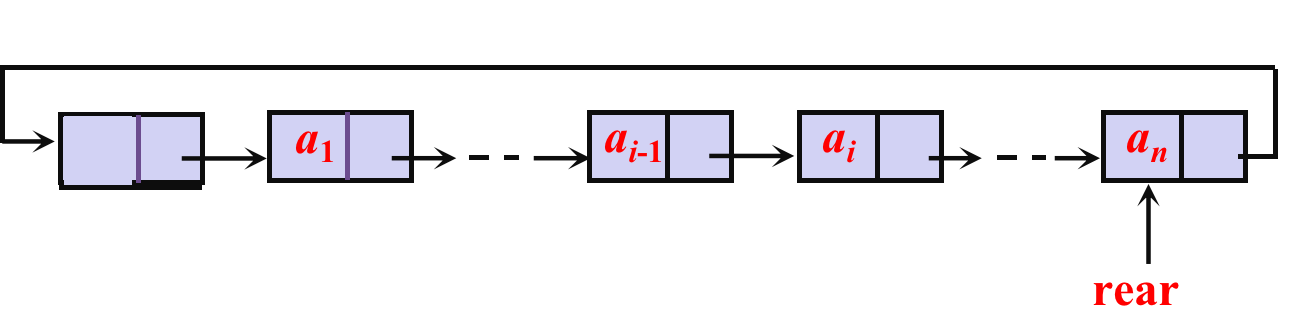
那么如何查找开始结点和终端结点?
答:开始结点:rear->next->next
终端结点:rear
1.1.2 循环链表的合并——单循环链表
下面是一个单循环链表:
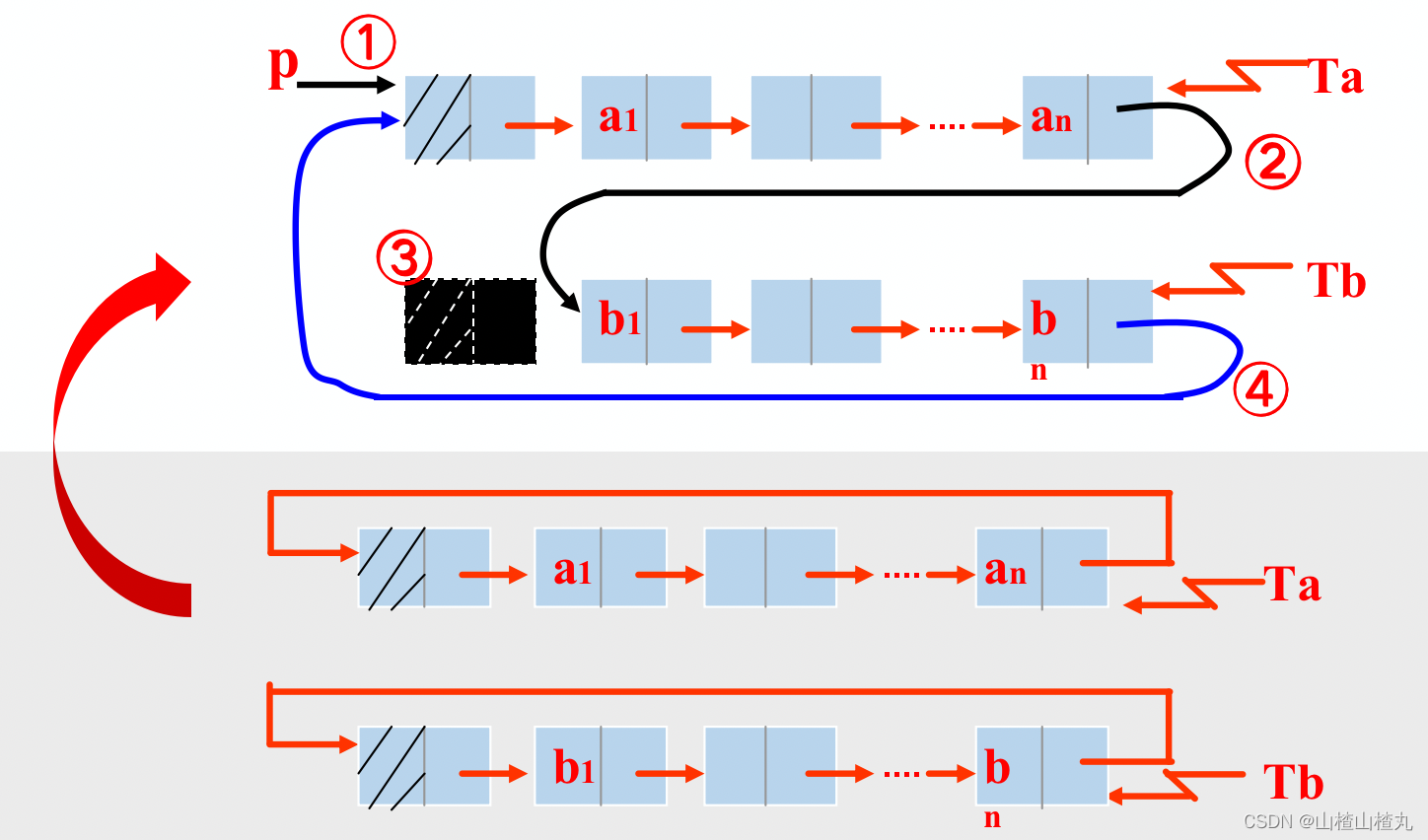
代码实现:
LinkList Connect(LinkList Ta,LinkList Tb)
{//假设Ta、Tb都是非空的单循环链表
p=Ta->next; //①p存表头结点
Ta->next =Tb->next->next; //②Tb表头连结Ta表尾
deleteTb->next; //③释放Tb表头结点
Tb->next=p; //④修改指针
return Tb;
}
总结:上述操作的时间复杂度为O(1)。
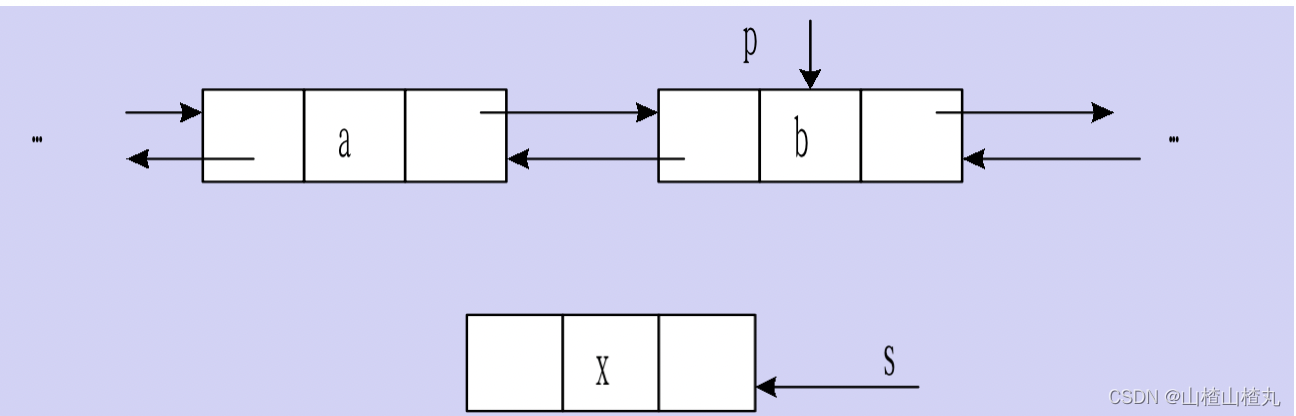
1.2 双向链表
如图所示:
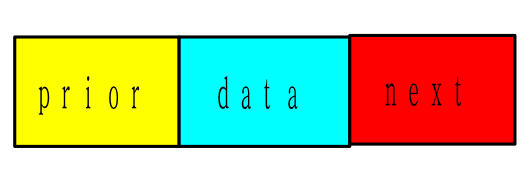
代码实现:
//---双向链表的存储结构---
typedef struct DuLNode{
ElemType data; //数据域
struct DuLNode *prior; //指向直接前驱
struct DuLNode *next; //指向直接后继
}DuLNode, *DuLinkList;
双向链表分为两种,如图所示,图b中有两个环,而图a中只有一个表头结点的空表。

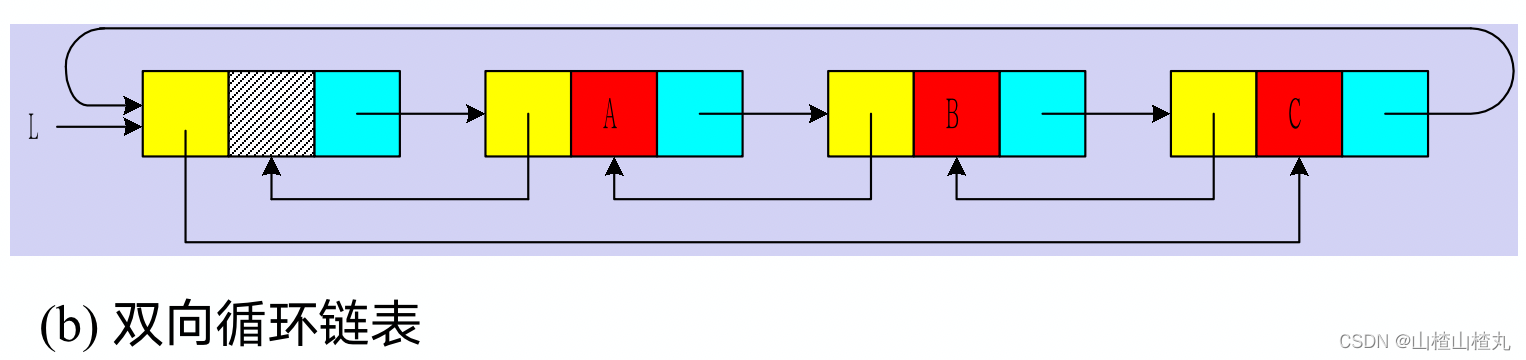
在双向链表中,若d为指向表中某一节点的指针:
d->next->prior = d->prior->next = d
1.2.1 双向链表的插入
代码实现:
Status ListInsert_DuL(DuLinkList &L,int i,ElemType e){
if(!(p=GetElemP_DuL(L,i))) return ERROR;
s=new DuLNode;
s->data=e;
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;
return OK;
}
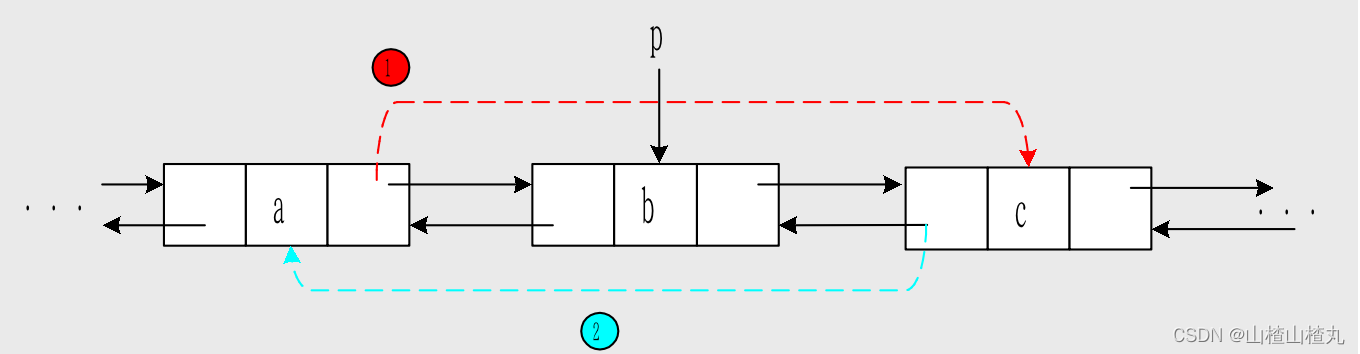
1.2.2 双向链表的删除
1. p->prior->next=p->next; 2. p->next->prior=p->prior;
代码实现:
Status ListDelete_DuL(DuLinkList &L,int i,ElemType &e)
{
if(!(p=GetElemP_DuL(L,i))) return ERROR;
e=p->data;
p->prior->next=p->next;
p->next->prior=p->prior;
delete p;
return OK;
}
四、顺序表和链表的比较
在实际应用中,我们不能说哪种的存储结构更好,由于它们各有优缺点,选用哪种存储结构,则应根据具体问题具体分析,通常从空间性能和时间性能两个方面作比较分析。
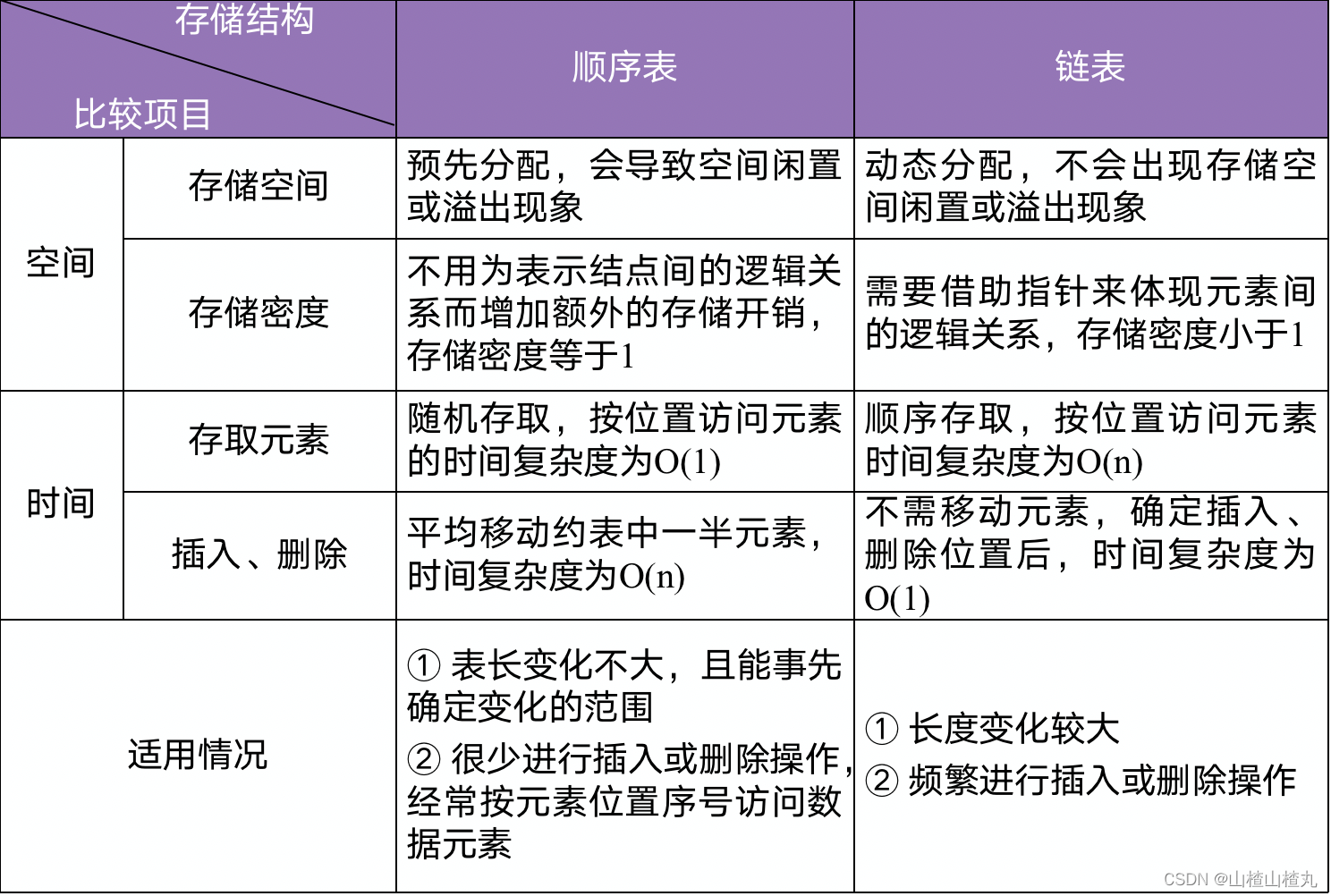
五、线性表的应用
5.1 线性表的合并
求解一般集合的并集问题:
问题:假设利用两个线性表La和Lb分别表示两个集合A和B,现要求一个新的集合: A=A B。例如, La=(7, 5, 3, 11) Lb=(2, 6, 3) 设合并后La=(7, 5, 3, 11, 2, 6)
步骤:
依次取出Lb 中的每个元素,执行以下操作:
1.在La中查找该元素;
2.如果找不到,则将其插入La的最后。
代码实现:
void union(List &La, List Lb){
La_len=ListLength(La);
Lb_len=ListLength(Lb);
for(i=1;i<=Lb_len;i++){
GetElem(Lb,i,e);
if(!LocateElem(La,e))
ListInsert(&La,++La_len,e);
}
}
时间复杂度为:
5.2 有序表的合并
有序表:线性表中的数据元素相互之间可以比较,且数据元素在线性表中依值非递减或非递增有序排列。
求解有序集合的并集问题:
问题:已知线性表La 和Lb中的数据元素按值非递减有序排列,现要求将La和Lb归并为一个新的线性表Lc,且Lc中的数据元素仍按值非递减有序排列。例如,
La=(1 ,7, 8) Lb=(2, 4, 6, 8, 10, 11) 则Lc=(1, 2, 4, 6, 7 , 8, 8, 10, 11)
步骤:
1. 创建一个空表Lc;
2. 依次从 La 或 Lb 中“摘取”元素值较小的结点插入到 Lc 表的最后,直至其中一个表变空为止;
3. 继续将 La 或 Lb 其中一个表的剩余结点插入在 Lc 表的最后。
代码实现:
void MergeList_Sq(SqList LA,SqList LB,SqList &LC){
pa=LA.elem; pb=LB.elem; //指针pa和pb的初值分别指向两个表的第一个元素
LC.length=LA.length+LB.length; //新表长度为待合并两表的长度之和
LC.elem=new ElemType[LC.length]; //为合并后的新表分配一个数组空间
pc=LC.elem; //指针pc指向新表的第一个元素
pa_last=LA.elem+LA.length-1; //指针pa_last指向LA表的最后一个元素
pb_last=LB.elem+LB.length-1; //指针pb_last指向LB表的最后一个元素
while(pa<=pa_last && pb<=pb_last){ //两个表都非空
if(*pa<=*pb) *pc++=*pa++; //依次“摘取”两表中值较小的结点
else *pc++=*pb++; } pa++; //LB表已到达表尾
while(pb<=pb_last) *pc+
while(pa<=pa_last) *pc++=*+=*pb++; //LA表已到达表尾
}//MergeList_Sq
时间复杂度/空间复杂度为:
有序表合并的优点:不需要开辟新的存储空间,可以使空间复杂度达到最低。
总结
以上就是本节所讲的内容,主要讲解链表的应用以及与顺序表的比较。希望各位大佬多多指点,我会在数据结构上一直持续更新下去!感谢佬们点支持!

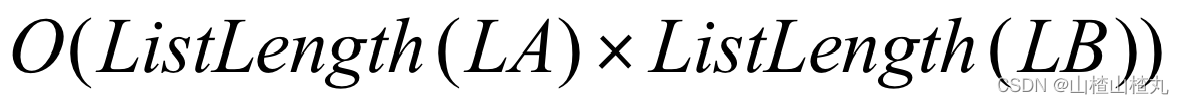
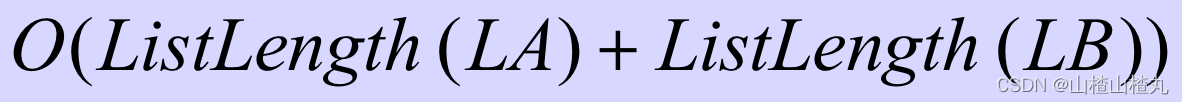



![[论文速览] Sparks of Artificial General Intelligence: Early experiments with GPT-4](https://img-blog.csdnimg.cn/e7a12c37a257461989e266da30a93bc6.png)