文章目录

复合系统与联合测量

一、张量积

二、复合系统的状态演化

---

复合系统与联合测量

拥有两个或两个以上的量子比特的量子系统通常被称为复合系统（composite systems）。单量子比特系统的描述与测量已有所了解，那么多个量子比特的系统该如何描述以及怎样去测量呢？单量子比特系统与多量子比特系统之间又有怎样的关系呢？首先，解决这些问题，需要认识一个新的运算-张量积（tensor products）。

 

一、张量积

张量积是两个向量空间形成一个更大向量空间的运算。在量子力学中，量子的状态由希尔伯特空间（Hilbert spaces）中的单位向量来描述。

设H1和H2分别为n1和n2维的希尔伯特空间.H1和H2的张量积为一个mn维的希尔伯特空间H=H1H2，对于H1中的每一个向量|h1〉和H2中的每一个向量|h2〉在H都有中唯一的向量|h1〉|h2〉，并且H中向量可表示为向量 |h1〉|h2〉的线性叠加。还要满足以下基本性质:

• 对任意|h1〉∈H1，|h2〉∈H2，以及任意复数c∈C，都有 

• 对任意，任意|h2〉∈H2，都有

• 对任意|h1〉∈H1，任意，都有

 

 |h1〉|h2〉经常被简写为|h1〉|h2〉，|h1,h2〉或|h1h2〉。

如果 |i〉和 |j〉分别为H1和H2的标准正交基，那么 |i〉 |j〉为H=H1H2的标准正交基。例如，现在有两个2维的希尔伯特空间H1和H2，并且都有一组标准正交基{ |0〉, |1〉}，那么H的标准正交基为{ |00〉, |01〉, |10〉, |11〉}。因此，任意给定H中的向量 |ψ〉都可以表示成这组标准正交基的线性组合

其中 。

 设A和B分别为H1和H2上的线性算子，那么算子AB作用到H中的任意向量

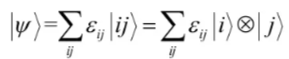
被定义为 

可以证明以这种方式定义AB为H1H2上的线性算子。

对于H中的两个任意向量和 ，这两个向量的内积被定义为

也可以证明这种函数满足之前的内积定义。

这样的表达形式优点是表示比较简练，缺点是不太容易有直观的认识。下面给出线性算子张量积的矩阵表示的运算规则-克罗内科积（Kronecker produet）。设A是m×n的矩阵，B是p×q的矩阵。AB的矩阵形式定义为

这里AB是一个mp×mq的矩阵，表示矩阵A的中的第i行，第j列元素与矩阵B相乘。
例如，Pauli矩阵和做张量积生成的矩阵为

举个反例就可以验证张量积并不满足交换律 。

可以看出

两个向量做张量积该如何表示呢？其实在给定基下，向量的坐标表示也可以看作一个特殊的矩阵。例如：向量在标准正交基{ |0〉, |1〉}下的矩阵表示分别为和。因此，的矩阵表示为

 

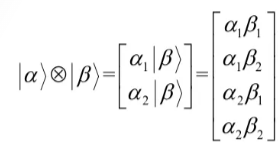
借助张量积，就可以由子系统来生成复合系统（Composite system）。
假设：复合物理系统的状态空间由子物理系统状态空间的张量积生成，即是说，如果有被1到n标记的系统，第i个系统的状态为，那么生成的整个系统的联合状态为。

复合系统有单量子系统不具有的另一个奇特现象就是纠缠（entanglement）。在数学
上，设态，若不存在，使得

则称 |ψ〉是纠缠的（entangled）。否则，称 |ψ〉不处于纠缠态（entangled state）。

例如，在双量子比特系统中，处于纠缠态。而是非纠缠的，这是因为还可分成。

 

二、复合系统的状态演化

已知两能级的量子系统的状态是通过西变换来实现演化的，那么复合系统的状态该如何随时间发生演化呢？复合系统可以看成是子系统的张成，因此以下假设可以说明复合系统中量子态的变化。

假设：复合系统中量子态的演化是由张成复合系统的子系统中量子态的演化对应的酉变换做张量生成的变换来描述，即是说，如果有被1到n标记的系统，第i个系统在t1时刻的状态为，那么生成的整个系统的联合状态为为；在t2时刻，通过酉变换将第i个系统的状态演化为，那么在t2时刻，复合系统的状态通过变换演化为。

例如，复合系统H由两能级系统H1和H2复合而成，在t1时刻，两个系统的状态都为|0〉，则复合系统的状态为|00〉；在时刻t2，，第一个系统经过X门，状态变为|1〉，第二个系统经过Z门，状态为|0〉，那么复合系统的状态经过变换

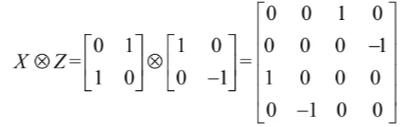
 变为

本质上复合系统中量子态的演化也是矩阵的乘法，与单个子系统相比，只不过是多了张量积的运算。

---

• 📢博客主页：https://lansonli.blog.csdn.net
• 📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正！
• 📢本文由 Lansonli 原创，首发于 CSDN博客🙉
• 📢停下休息的时候不要忘了别人还在奔跑，希望大家抓紧时间学习，全力奔赴更美好的生活✨