从理论上讲,只要对随机现象进行足够多次的试验,被研究的随机现象的规律
性就能清楚地呈现出来. 但实际上,试验的次数只能是有限的,有时甚至是很少
的,因为采集某些数据时,常要将研究的对象破坏.例如,观测灯泡的寿命时,就一
定要把它用坏;检查炮弹性能时,就需要将它发射出去.有时即使不破坏对象,时
间、财力和人力也不允许.特别当信息具有很强的时效性时,旷日待久的大量检查
或试验,只能获得陈旧的、毫无意义的信息.因此,数理统计要研究的问题便是怎样
选择有效的抽样方法采集数据(抽样),并利用抽样获得的有限数据,对被研究的随
机现象的规律性作出尽可能精确而可靠的结论(推断).
在数理统计中研究的基本问题有四个:参数估计、假设检验、方差分析和回归
分析为此,先引入几个基本概念.
1.1 总体与样本
在数理统计中,通常把所研究对象的全体称为总体(或母体),而把组成总体的
每个元素称为个体.例如,某工厂生产的灯泡的寿命就是一个总体,而每个灯泡的
寿命则是一个个体.
代表总体的指标(如灯泡寿命、钢筋强度等)的取值都有一定的随机性,因此,
它们都是随机变量.所以,总体就是某个随机变量可能取值的全体,常用X,Y,Z
(或)等表示.总体的概率分布就是该随机变量的概率分布.
从总体X中抽取一个个体,就是对代表总体的随机变量X进行一次试验(观
测). 从总体中随机地抽取n个个体:
![]()
就是对随机变量X进行了一组试验.通常把由这n 个试验组成的试验组(1.1)称
为总体X的一个样本(或子样),样本中个体的数目n称为样本容量,其中称为
样本的第i个分量.
由于每个都是从总体X中随机抽取的, 在抽取之前,它可能取得X所有可能取值中的任何一个, 可见这里的每个
都是一个随机变量, 因此
就是一个n维随机变量.在抽取之后,每一个
的值已完全确定,它是一个数,是对
的一次观测值,记作
这时称
![]()
为样本(1.1)的一个观测值,简称样本观测值.
我们抽取样本的目的是为了对总体的分布进行分析和推断.因此要求抽样具有代表性,即应使总体的每个个体都有同等的机会被抽到,或每个样本分量都与总体X 有相同的概率分布.此外,还要求抽样必须是独立的, 即要求样本
为相互独立的随机变量,或每个分量的观测结果不影响其他分量的观测结果,也不受其他观测结果的影响.这样抽取的样本称为简单随机样本.获得简单随机样本的方法称为简单随机抽样,今后,凡是提到样本和抽样,都是指简单随机样本和简单随机抽样.
1.2 统计量和样本矩
样本来自总体,是总体的代表,是统计推断的依据.但是我们抽取样本之后,并不直接用样本进行推断,而常需要对样本进行一番加工和提炼,把样本中包含的我们所关心的信息集中起来,以便对总体的某种特性作出推断.
例如,当我们取得总体X的一个样本时,常构造样本的平均值

来推断总体的均值当然, 为了推断总体的其他特性,还要用到样本的其他函数.为此,我们引入下面的定义.
定义1. 1. 1 设是来自总体X的一个样本,如果函数
为
的一个实值函数,且
中不包含任何未知参数,那么称
为一个统计量。
由于构成统计量(1.3)的的实随机变量,所以,作为n维随机变量的函数,统计量也是随机变量.
若为样本
的一个观察值,则成
![]()
为统计量(1. 3)的一个观测值.
例1 设为来自正态总体
的样本,则当
已知,
未知时,样本均值
和
![]()
都是统计量,而

不是统计量(因为它包含未知参数).
数理统计中,常用的统计量有

它们分别称为样本均值、样本方差、样本标准差、样本K阶原点矩和样本K阶中心矩. 当取为样本
的观测值时,这些统计量的观测值分别为
’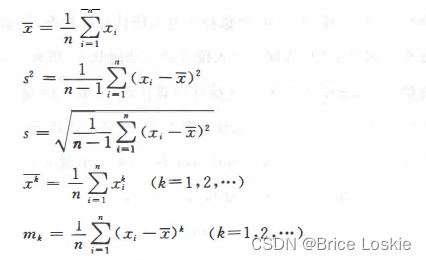
显然上述统计量之间有如下的关系:
![]()
应用中还有一种常用的统计量称为次序统计量.设是取自总体X的样本,
是相应的观测值,把它们由小到大排列并用
表示,即
![]()
取值为的变量都是
的函数,记作
显然,都是统计量,称它们为次序统计量,其中的
称为最小次序统计量,
称为最大次序统计量,次序统计量满足关系
![]()
它们的观测值为,由次序统计量构成的
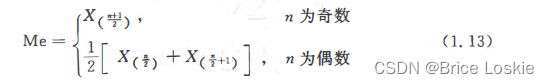
和
![]()
分别称为样本中位数和样本极差.

![[Linux]-----进程信号](https://img-blog.csdnimg.cn/bf51c777a0bf45dba1719dc2ecbe260c.png)