在番茄风控往期的内容中,我们一直在跟大家介绍风控策略干货内容,相关内容包括:
①风控的拒绝捞回策略
②多规则的策略筛选
③策略的调优
④策略的开发与应用
…
策略相关的内容可谓干货满满,比如关于策略开发与应用的内容上,我们跟大家详细介绍了三大最佳策略的筛选方法有:
①单维的策略的开发
②二维特征交叉组合开发
③多维特征决策树模型等策略开发的内容
详细的内容参考如下:
①单维特征标签分布
首先来介绍单维特征标签分布的方式。这种方法的原理逻辑是将某特征变量进行分箱处理,然后根据不同区间的数据表现来决定是否作为规则,其中样本数据表现主要包含两个维度,分别为坏账率(badrate)与占比(percent)。
一般情况下,区间样本坏账率要达到整体样本坏账率的23倍以上,区间样本占比最好保持在1%5%范围内。此外,样本分布趋势最好满足单调性,这样符合实际业务理解,而且规则区间选择尽量是左边界或右边界的范围,可以有效保证策略在后期的稳定性与合理性。
这里以某特征X10(贷前申请信用风险评分)为例,来看下变量的分布情况,具体实现过程与输出结果分别如1所示:
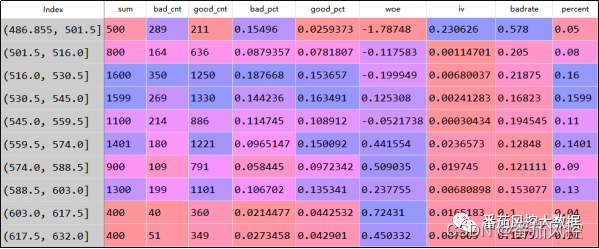
图1 单维特征分布结果
由特征分布结果可知,边界区间(486,501]范围内样本坏账率badrate达到57.8%,是整体样本坏账率18.65%(图5)的3倍以上,说明此区间样本群体的风险很高,而且样本占比也仅有5%,满足策略制定的基本条件。此外,从指标分布的趋势可以直观看出,随着X10(贷前申请信用风险评分)的增加,坏账率badrate整体呈现下降趋势,具有一定单调性而且满足实际业务理解。综上分析,特征X10可以开发出的策略规则为“当贷前申请信用风险评分(X10)<=501时,拒绝”。
根据以上分析方法,对于其他单维度特征,可以按照这个分析思路来分别探索策略规则,此处不再详细展开。
②二维特征交叉组合
二维特征的策略开发,原理逻辑是采用决策矩阵的思想来实现,也就是将两个离散化处理后的特征进行二维交叉,然后根据每个组合单元的数据表现来决定是否可以作为规则,其中数据表现与单维度分析方法一样,也是通过单元组合下样本的坏账率(badrate)与占比(percent)来分析。
二维特征交叉组合的原理结构如图2所示,这里需要注意的是,在选取某个组合作为策略规则时,最好是矩阵表的边角组合,可以是单个多区间,例如示意图中的X1-bin1与X2-bin1组合、X1-bin4与X2-bin4组合等,其原因是为了保证规则的业务解释性与分布稳定性。
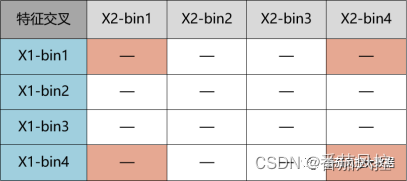
图2 二维交叉组合原理
这里我们以特征X03(在我司贷款逾期最高天数)与X08(欺诈风险等级)为例,来介绍下二维特征交叉规则的原理逻辑。针对这2个特征的二维矩阵实现的输出分布结果如图3所示。
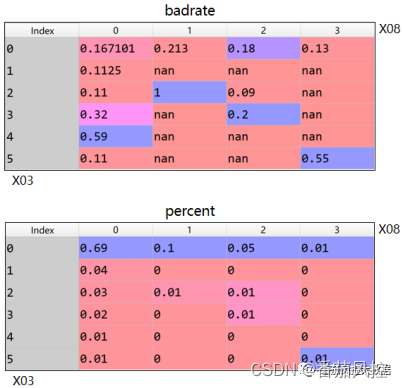
图3 二维特征交叉结果
由以上特征X03与X08的交叉结果指标(badrate与percent)分布可以看出,X03=5与X08=3交叉组合下样本群体的坏账率badrate达到55%,约为整体样本坏账率(18.65%)的3倍,而且样本占比仅有1%,满足二维特征规则开发的指标分布条件。同时,此区间对应X03与X08取值,在场景理解上也是完全满足业务逻辑的,也就是X03(在我司贷款逾期最高天数)与X08(欺诈风险等级)的取值越大风险表现越高。综上分析,根据特征X03与X08开发出的二维规则为“在我司贷款逾期最高天数(X03)>=5,且欺诈风险等级(X08)>=3,拒绝”。
对于其他特征二维组合,可以按照以上分析逻辑来实现,其中有个细节需要说明,针对连续型特征的交叉组合,在构建矩阵之前一定要对特征进行分箱离散化处理,然后根据离散区间来实现二维特征的决策矩阵。
③ 多维特征决策树模型
多维特征的综合策略开发,决策树模型是非常有效一种实现方式,不仅原理逻辑简单,而且实现过程也较为方便。但是,在特征变量较多的情况下,采用决策树开发策略规则时,模型参数max_depth(树的深度)不要设置太大,主要原因是这样的规则虽然从区分度结果表现来看是比较好的,但在后期应用过程中很容易出现波动的情况,这是由于规则的特征复杂度引起的。因此,通过决策树模型算法开发规则时,参数max_depth最好定义在3~10范围之内。此外,模型训练拟合的特征变量,最好是经过特征工程筛选后的性能较优字段。
这里我们采用决策树回归算法来实现多维特征策略规则的开发,模型训练的拟合变量为X01~X10,最终输出的决策树结果通过可视化展示如图3所示。
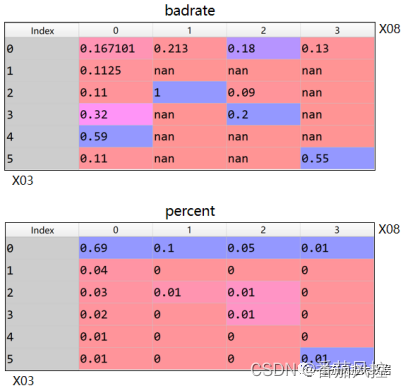
图3 多维特征决策树结
以上在相关的规则开发上线后,运营了一段时间后,我们便需要观察相关的策略,在客群的后续表现与相关的资产表现情况。如果上线的策略不合适,便需要进行相关的调整与优化。
策略生成过程中,还有很多的关于多规则策略执行中的细节,有兴趣的童鞋可继续关注课程:
《风控策略进阶篇—以最小化风险提升通过率的技巧》

…
~原创文章