3.1 机器学习 — 决策树

一 金融评分卡

• 模型做好后尽量快的上线，以符合要求的模型，尽快上线。
• 超参数赋予权重，使得模型的参数不一致，而达到均衡样本数据

二 决策树原理

1. 找女朋友

• 性别：男 女
• 年龄：20-23 非20-23
• 学历：高中以上 高中以下
• 颜值：>=75 <75
• 子女状况：无 有
• 恋爱经历：5段以下 5段及以上
• 负债情况：10万以下 10万及以上
• 相处到结婚：3-4年 非3-4年
• 是否接收异地恋：可以 不可以
• 是否接受控制欲比较强的：接受 不接受
• 财政大全在谁的手中：接受 不接受
• 养老负担 ： 两个及以下 两个以上
  以上都是对标签值进行二分类

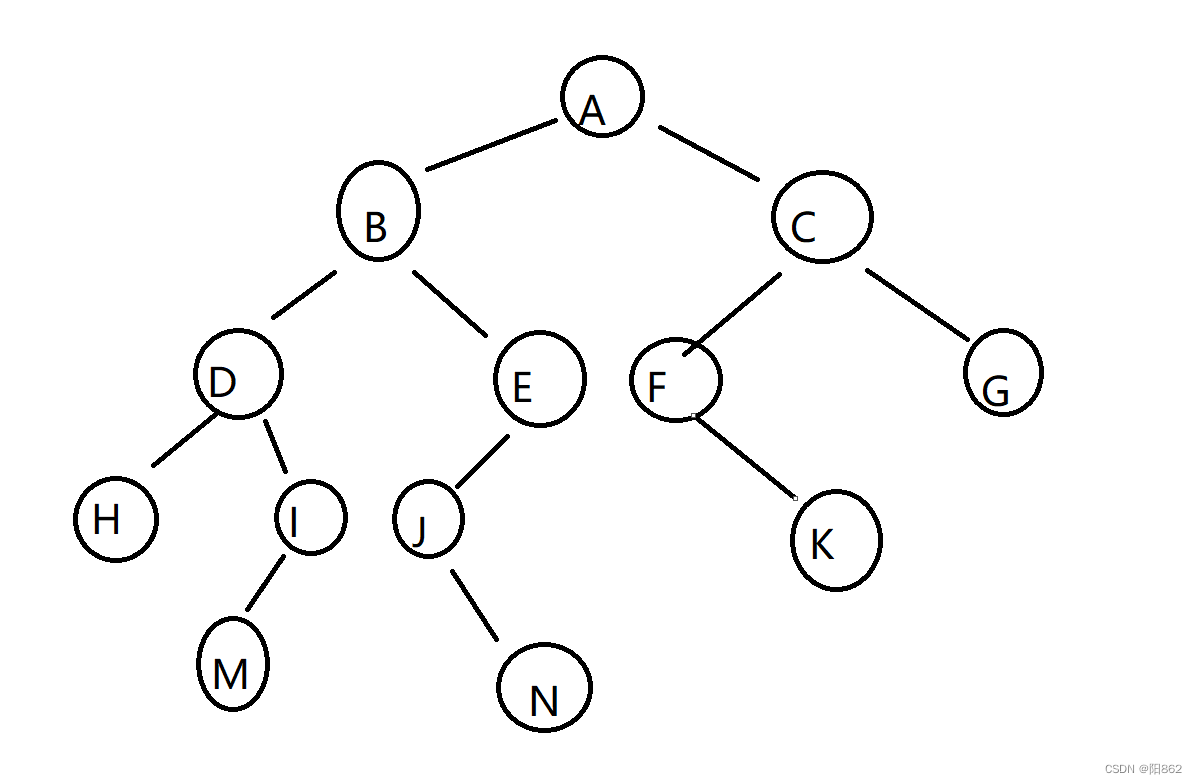
2. 决策树定义

决策树的定义：决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

决策树的特点：可以看到，决策树的决策过程非常直观，容易被人理解。目前决策树已经成功运用于医学、制造产业、天文学、分支生物学以及商业等诸多领域。之前介绍的K-近邻算法可以完成很多分类任务，但是它最大的缺点就是无法给出数据的内在含义，决策树的主要优势就在于数据形式非常容易理解。决策树算法能够读取数据集合，构建类似于上面的决策树。决策树很多任务都是为了数据中所蕴含的知识信息，因此决策树可以使用不熟悉的数据集合，并从中提

• 过程非常直观，易于理解
  • 黑盒模型 ：对输出的结果不清楚原理，只是知道结果，可解释性不强。
  • 百盒模型/灰盒模型：清楚训练原理，对结果的产生可解释性强

不同于逻辑斯蒂回归和贝叶斯算法，决策树的构造过程不依赖领域知识，它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支，其目标是让各个分裂子集尽+可能地"纯"。尽可能"纯"就是尽量让一个分裂子集中待分类项属于同一类别。
简而言之，决策树的划分原则就是:将无序的数据变得更加有序

分裂属性分为三种不同的情况:
属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试，按照"属于此子集"和"不属此子集"分成两个分支
·属性是连续值。

三 ID3、C4.5、CART

这个概念最早起源于物理学，在物理学中是用来度量一个热力学系统的无序程度。而在信息学里面，嫡是对不确定性的度量。在1948年，**香农引入了信息嫡，将其定义为离散随机事件出现的概率，一个系统越是有序，信息嫡就越低，反之一个系统越是混乱，它的信息嫡就越高。**所以信息嫡可以被认为是系统有序化程度的一个度量。
在可以评测哪种数据划分方式是最好的数据划分之前，我们必须学习如何计算信息增益。集合信息的度量方式称为香农嫡或者简称为嫡,这个名字来源于信息论之父克劳德·香农
嫡定义为信息的期望值，在明晰这个概念之前，我们必须知道信息的定义。如果待分类的事务可能划分在多个分类之中，则符号x的信息定义为:

先处理熵高的，即先处理混乱程度大的。

**信息增益：**在划分数据集之前之后信息发生的变化称为信息增益。
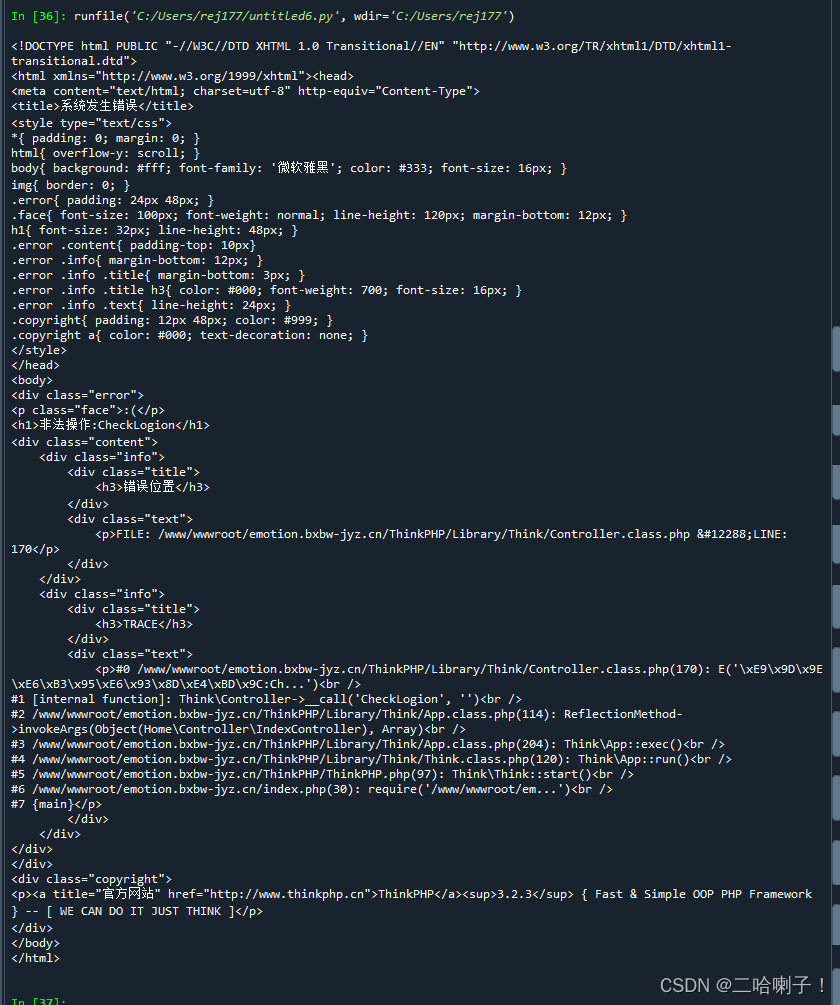
我们可以使用多种方法划分数据集，但是每种方法都有各自的优缺点。组织杂乱无章数据的一种方法就是使用信息论度量信息，信息论是量化处理信息的分支科学。我们可以在划分数据之前使用信息论量化度量信息的内容。知道如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。

ID3算法的优缺点：

优点

• 方法简单、计算量小、理论清晰、学习能力较强、比较适用于处理规模较大的学习问题。

缺点

• 倾向于选择那些属性取值比较多的属性，在实际的应用中往往取值比较多的属性对分类没有太大价值、不能对连续属性进行处理、对噪声数据比较敏感、需计算每一个属性的信息增益值、计算代价较高。由于信息增益的不稳定性，容易倾向于众数属性导致过度拟合，算法抗干扰能力差。

其他常见算法

• CLS 算法：是最原始的决策树分类算法，基本流程是，从一棵空数出发，不断的从决策表选取属性加入数的生长过程中，直到决策树可以满足分类要求为止。CLS算法存在的主要问题是在新增属性选取时有很大的随机性。ID3算法是对CLS算法的改进，主要是摒弃了属性选择的随机性。

• C4.5 算法

  基于ID3算法的改进，主要包括:使用信息增益比替换了信息增益下降度作为属性选择的标准;在决策树构造的同时进行剪枝操作;避免了树的过度拟合情况;可以对不完整属性和连续型数据进行处理;使用k交叉验证降低了计算复杂度;针对数据构成形式，提升了算法的普适性。

• CART树

  
  

四 决策树代码实现

1 . 信息增益 ID3

import math
import numpy as np

# 账号是否真实
# p(no) = 3/10
# p(yes) = 7/10

# np yes
info_D= -0.3*math.log2(0.3) - 0.7*math.log2(0.7)
info_D  #  0.8812908992306927

## 1. 日志密度
# 1.按照日志密度进行划分
info_s = -(2/3)*math.log2(2/3) - (1/3)*math.log2(1/3)
info_l = -1*math.log2(1)
info_m = -(1/4)*math.log2(1/4)-(3/4)*math.log2(3/4)

# 日志密度
info_L_D = 0.3*info_s+0.3*info_l+0.4*info_m
info_L_D  # 0.6

## 按照日志密度的信息增益
info_D - info_L_D   #0.2812908992306927

# 按照好友密度的信息增益
info_s1 = -(1/4)*math.log2(1/4) - (3/4)*math.log2(3/4)
info_l1 = -1*math.log2(1)
info_m1 = -1*math.log2(1)
info_L_D1 = 0.4*info_s1 +0.2*info_l1 + 0.4*info_m1
info_D - info_L_D1   # 0.5567796494470396

# 按照真实头像的信息增益
info_n= -(2/5)*math.log2(2/5)-(3/5)*math.log2(3/5)
info_y=-(4/5)*math.log2(4/5)-(1/5)*math.log2(1/5)
info_YN = 0.5*info_y +0.5*info_n
info_D - info_YN  # 0.034851554559677256

# 将sl看做一类，m看做另一类，计算信息增益
info_sl = -(4/6)*math.log2(4/6) - (2/6)*math.log2(2/6)
info_m = -(3/4)*math.log2(3/4) - (1/4)*math.log2(1/4)
info_al_m = 0.6*info_sl +0.4*info_m

# # 日志密度的信息增益
info_D - info_al_m  # 0.0058021490143458365

2. 决策树的基本使用

from sklearn.tree import DecisionTreeClassifier
# 基于CART的树模型 既可以解决回归问题也可以解决分类问题 只能划分二叉树
DecisionTreeClassifier()

各参数：

• criterion：gini或者entropy,前者是基尼系数，后者是信息熵。

• splitter： best or random 前者是在所有特征中找最好的切分点后者是在部分特征中，默认的”best”适合样 本量不大的时候，而如果样本数据量非常大，此时决策树构建推荐”random” 。

• max_features：None（所有），log2，sqrt，N 特征小于50的时候一般使用所有的

• max_depth： int or None, optional (default=None) 设置决策随机森林中的决策树的最大深度，深度越 --> 大，越容易过拟合，推荐树的深度为：5-20之间。

• min_samples_split：设置结点的最小样本数量，当样本数量可能小于此值时，结点将不会在划分。

• min_samples_leaf： 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟 节点一起被剪枝。

• min_weight_fraction_leaf： 这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄 弟节点一起被剪枝默认是0，就是不考虑权重问题。

• max_leaf_nodes： 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点 数。

• class_weight： 指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多导致训练的决策树过 于偏向这些类别。这里可以自己指定各个样本的权重，如果使用“balanced”，则算法会自己计算权重，样本量 少的类别所对应的样本权重会高。

• min_impurity_split： 这个值限制了决策树的增长，如果某节点的不纯度(基尼系数，信息增益，均方差，绝 对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。

• 所有的参数都是为了减少复杂度，防止过拟合

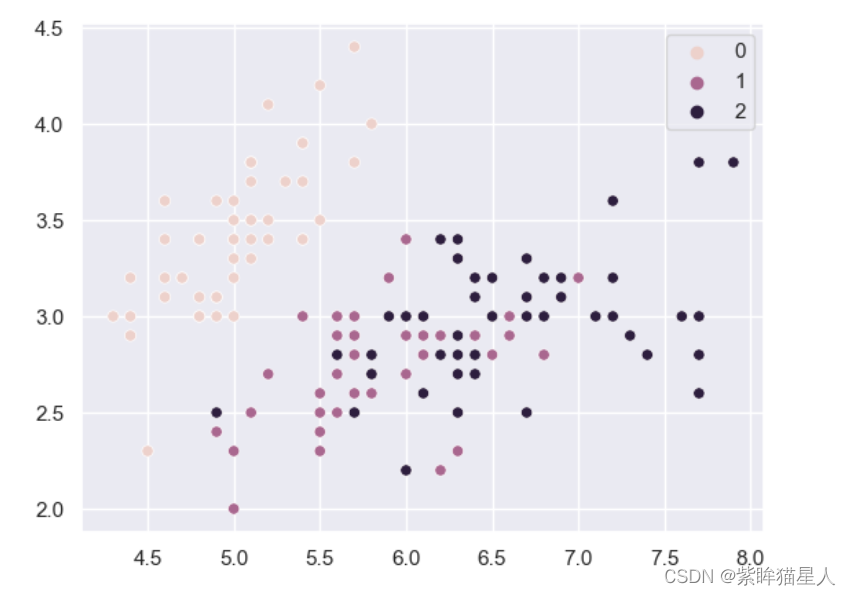
  from sklearn.datasets import load_iris
  import numpy as np
  import pandas as pd
  from pandas import Series,DataFrame
  
  import matplotlib.pyplot as plt
  import seaborn as sns
  %matplotlib inline
  # 使用鸢尾花数据集
  iris = load_iris()
  data  = iris.data
  target = iris.target
  feature_names = iris.feature_names
  target_names = iris.target_names
  # 通过前两个特征进行二维化展示
  sns.set()
  sns.scatterplot(x=data[:,0],y=data[:,1],hue=target)
  

# 首先制作DataFrame
iris_df= DataFrame(data=data,columns=feature_names)
iris_df.head()
# 需要新增一个类别情况 # 相当于制作标签
iris_df['cate']=Series(target).map(lambda x:target_names[x])
iris_df.head()
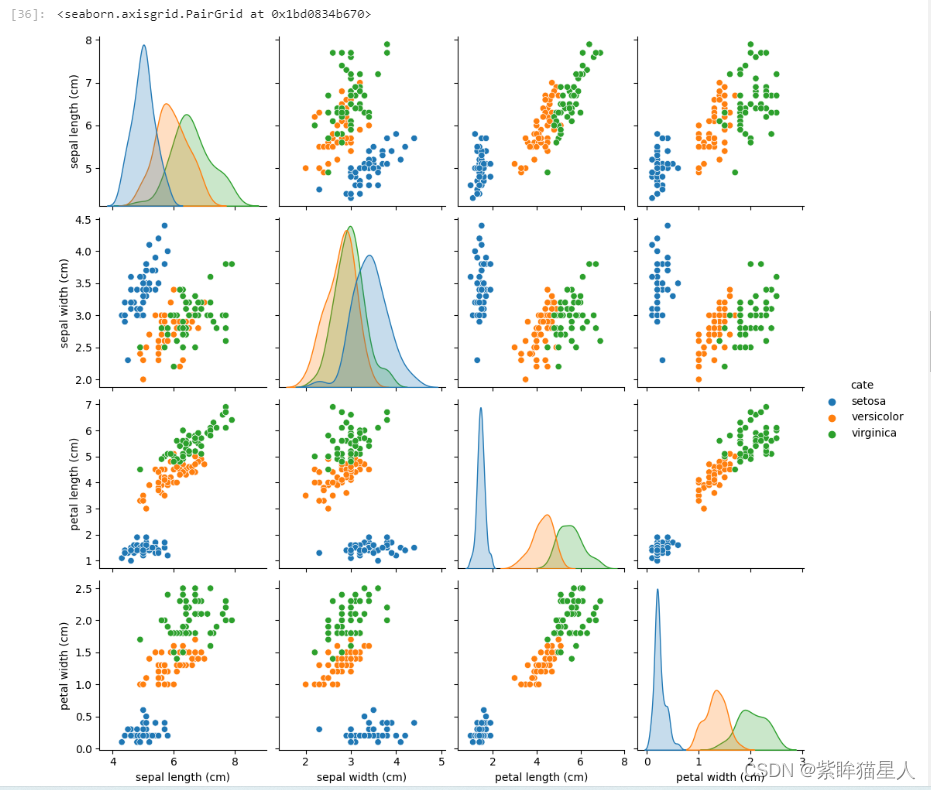
# 特征两两之间关系绘图
sns.pairplot(data=iris_df,hue='cate')

# 假设取前两列进行建模
X=iris_df.iloc[:,:2].copy()
y = iris_df.iloc[:,-1].copy()

# 拿 knn做对比
from sklearn.neighbors import KNeighborsClassifier

# 评判knn的训练误差或经验误差
knn.score(X,y)

# 对比 ：使用决策树建模
dt = DecisionTreeClassifier()
dt.fit(X,y)

# 评判  # 训练误差高，实际上是过拟合
dt.score(X,y)

# 尝试使用4个特征进行建模
dt2 = DecisionTreeClassifier()
dt2.fit(data,target)

# 究极过拟合，说明决策树如果不加限制，是很容易过拟合的。
dt2.score(data,target)  # 1.0

# 定义函数展示决策边界
def show_edge(model,X,y):
    xmin,xmax = X.values[:,0].min(),X.values[:,0].max()
    ymin,ymax = X.values[:,1].min(),X.values[:,1].max()
    
    a = np.linspace(xmin,xmax,200)
    b = np.linspace(ymin,ymax,200)
    xx,yy =np.meshgrid(a,b)
    
    X_test = np.c_[xx.ravel(),yy.ravel()]
    
    model.fit(X,y)
    y_ = model.predict(X_test)
    
    plt.scatter(X_test[:,0],X_test[:,1],c=y_,cmap=plt.cm.Accent)
    plt.scatter(X.values[:,0],X.values[:,1],c=y,cmap=plt.cm.Blues)
    plt.xlabel(X.columns[0])
    plt.ylabel(X.columns[1])
    
dt = KNeighborsClassifier()
show_edge(dt,X,target)

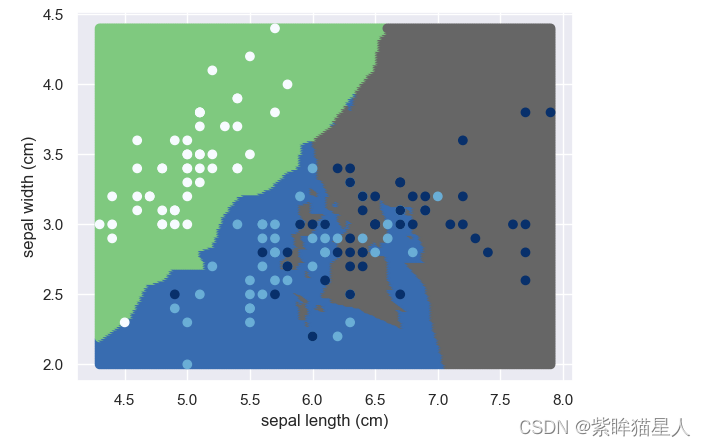
dt = DecisionTreeClassifier()
show_edge(dt,X,target)

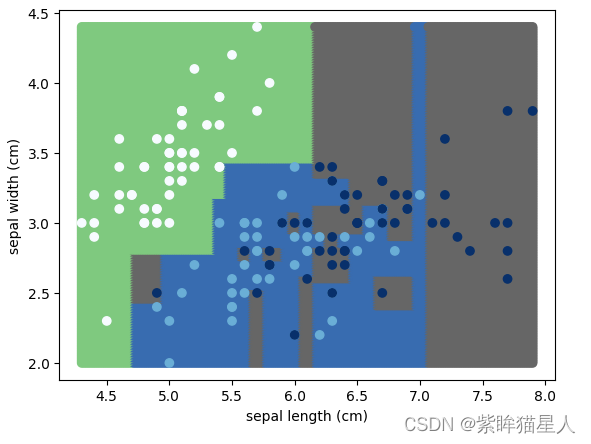
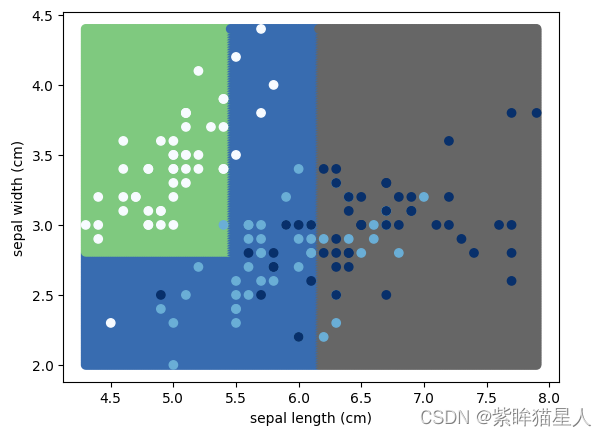
# 限制深度
dt1 = DecisionTreeClassifier(max_depth=2)
show_edge(dt1,X,target)

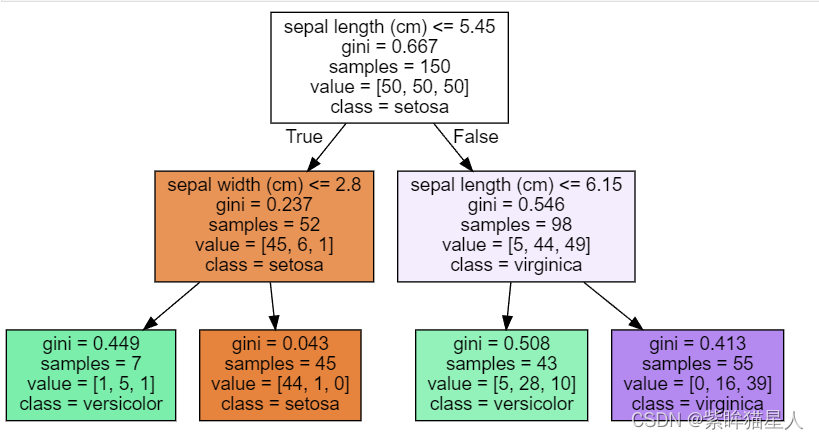
• 决策树的可视化
  • 在jupyter lab 上安装 %pip install graphviz
  • 安装该程序
  • 在cmd 输入dot -version （查看是否安装成功）
  • 在jupyter lab 上如果显示dot 环境未配置好，就重启一下电脑。

     import graphviz
     from sklearn import tree
     
     data.shape
     dot = tree.export_graphviz(dt1,out_file=None,feature_names=X.columns,class_names=target_names,filled=True)
     graphviz.Source(dot)

3. 决策树回归

import numpy as np
import pandas as pd
from pandas import Series,DataFrame

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

from sklearn.tree import DecisionTreeRegressor
# 决策树回归
# 波士顿房价
from sklearn.datasets import load_boston

boston = load_boston()
target = boston.target

data = boston.data
target = boston.target

from sklearn.model_selection import train_test_split

# 切分
x_train,x_test,y_train,y_test = train_test_split(data,target,test_size=0.2,random_state=1)

# 决策树回归
dt_rgr = DecisionTreeRegressor()
dt_rgr.fit(x_train,y_train)

# 评判回归 mse
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,dt_rgr.predict(x_test))

• 思考：

  # R²应该怎么用？
  # 1.metrcics
  # 2. score
  from sklearn.metrics import r2_score
  

4. 使用数模型的回归来完成多输出问题

 # 0-1一共200个数据统一乘上200再减去100 使得范围成为-100 到 100通过排序构造成特征
X = np.sort(np.random.random(size=200)*200-100).reshape (-1,1)

# 构造偏差
bias = np.random.random(size=200)*0.5-0.25
bias = bias.reshape(-1,1)

# 构造y
y = np.sin(X)+bias
x = np.cos(X)
Y = np.concatenate((x,y),axis=1)

# 弧度转角度
(X*180/(np.pi)%360).astype(np.int8)

plt.scatter(Y[:,0],Y[:,1],color='green')
plt.axis('equal')
plt.show()

# 借助Dt决策进行多输出拟合
# X需要二维数组
# y需要一维或者多维数组
dt = DecisionTreeRegressor()
dt.fit(X,Y)

X_test = np.linspace(-100,100,100).reshape(-1,1)
Y_ = dt.predict(X_test)

# 绘制结果
plt.scatter(Y[:,0],Y[:,1])
plt.axis('equal')
plt.show()

# 查看多个决策树的深度的拟合效果
depth_list = [2,7,18,None]
plt.figure(figsize=(16,4))

for index ,depth in enumerate(depth_list):
    dt = DecisionTreeRegressor(max_depth=depth)
    dt.fit(X,Y)
    
    X_test = np.linspace(-100,100,100).reshape(-1,1)
    Y_ =dt.predict(X_test)
    
    axes = plt.subplot(1,len(depth_list),index+1)
    plt.scatter(Y_[:,0],Y_[:,1])
    plt.axis('equal')
    plt.title('max_depth:{}'.format(depth))
plt.show()

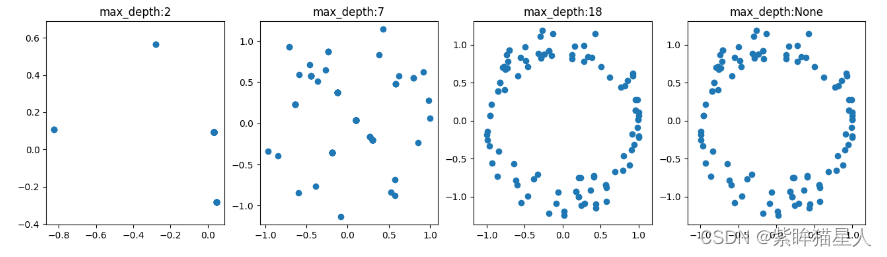
五 决策树的优缺点

• 优点:
  • 决策树有利于理解，可解释性好。可以进行可视化分析，容易提取出规则。比较适合处理有缺失属性的样本。测试数据集时，运行速度较快。
• 缺点:
  • 容易发生过拟合。(集成学习模型特别是随机森林可以一定程度上防止过拟合)容易忽略数据集中属性的相互关联。

六 过拟合和解决办法

过拟合：过拟合:决策树生成算法递归的产生决策树，直到不能继续下去为止，这样产生的树往往对训练数据的分类很准确，但对未知测试数据的分类缺没有那么精确，即会出现过拟合现象。过拟贪产生的原因在于在学习时过多的考虑如何提高对训练数据的正确分类，从而构建出过于复杂的决策树，解决方法是考虑决策树的复杂度，对已经生成的树进行简化。
例如，决策树永远可以把N个数据分成100%纯洁的N组，如果在『日期』这个条件下做分裂，就完犊子了。

解决办法：

限制分裂次数（没有必要的分裂不要去分裂）、限制分裂层数，让决策树的复杂度降低，从而使得产生的模型可以适用于大多数。

• 没必要的分裂不要整
• 树减枝Prune: 从已经生成的树上裁掉一些子树或叶节点，并将其根节点或父节点作为新的叶子节点，从而简化分类树模型。

口述cls id3 c4.5 cart的各种特点