文章目录
- 0. 前言
- 1. 链表的中间节点
- 2. 链表中倒数第k个结点
- 3. 链表分割
- 4. 链表的回文结构
- 5. 相交链表
- 6. 结语
0. 前言
书接上回,我们这次依然是为大家带来链表的OJ题。这一次的题量比之前多一些,内容为链表的中间节点、链表中倒数第k个节点、链表分割、链表的回文结构、相交链表。同样的,我也会使用多种方法和图解来帮助大家更容易理解、吃透这些题目。题目的难度和代码量会有些上升,但是内容也更加丰富,坚持看完,你会有意想不到的收获!话不多说,我们这就开始。
1. 链表的中间节点
链接:876. 链表的中间结点
描述:
给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
示例1:
输入:[1,2,3,4,5]
输出:此列表中的结点 3 (序列化形式:[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意,我们返回了一个 ListNode 类型的对象 ans,这样:
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例2::
输入:[1,2,3,4,5,6]
输出:此列表中的结点 4 (序列化形式:[4,5,6])
由于该列表有两个中间结点,值分别为 3 和 4,我们返回第二个结点。
提示:
- 给定链表的结点数介于
1和100之间。
思路1:
第一种思路是 暴力求解 。
题目不是要求链表的中间节点吗?那么我遍历链表,直接算出链表的长度。
对于奇数个节点,那么我返回 长度 / 2的节点当然没问题,且题目要求,如果有两个中间节点,则返回第二个中间节点。那不正好,我偶数个节点时 长度 / 2 就是中间第二个节点,这不就秒了吗(doge)。

但是如果只能遍历一遍呢?我们能用什么方法解决?看思路2↓
思路2(精讲):
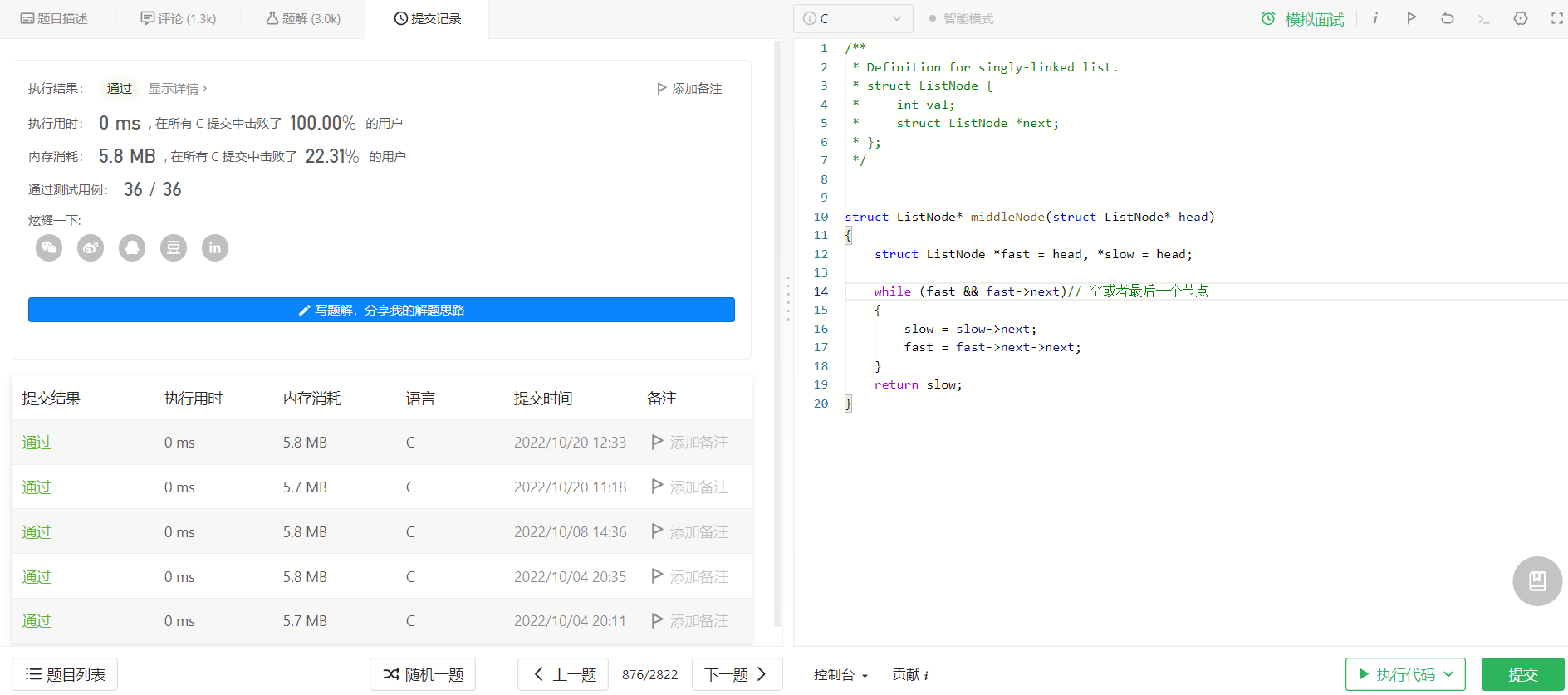
这里采用的思路为快慢指针。
方法是这样的,给定一个慢指针 slow 一次走一步,快指针 fast 一次走两步。快指针的速度是慢指针的2倍。
当链表的节点数为 奇数 时,快指针走到链表 最后一个节点 停止;当链表的节点数为 偶数 时。快指针走到 空指针 停止。
最后返回的 slow 就是中间节点。
这里的原理其实就是利用了一个差值的原理,当快指针走完链表,那么慢指针恰好走了它的一半,它们走的时间一样,那么慢指针就是中间节点的位置。

2. 链表中倒数第k个结点
链接:链表中倒数第k个结点
描述:
输入一个链表,输出该链表中倒数第k个结点。
示例1::
输入:
1,{1,2,3,4,5}
返回值:
{5}
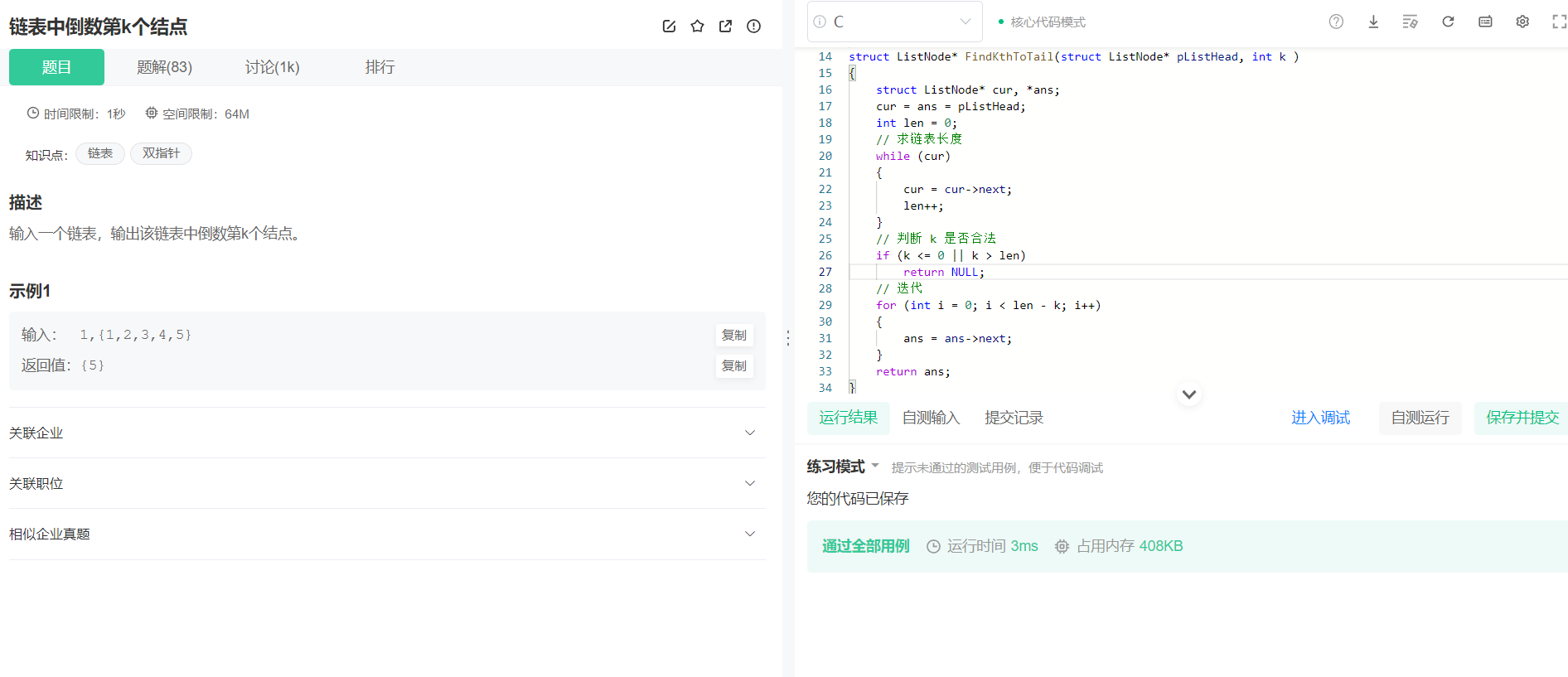
思路1:
和求链表的中间节点的方法相似,为直接法。
要求链表的倒数第 k 个节点,那么就是删除链表正数第 len(链表长度) - k + 1 个节点。
举个例子,例如链表长度为 5,删除倒数第 2 个节点,就是删除链表正数第 4 个节点,推导出来就是第 len + 1 - k 个节点。
所以只要先算出链表长度,然后遍历到 len + 1 - k 个节点返回即可。
但是这里需要注意一下区间和迭代关系。
既然这道题目也可以用直接法,那么能否也适用于快慢指针?这当然可以,而且这道题的方法也很巧妙,接下来看思路2↓
思路2(精讲):
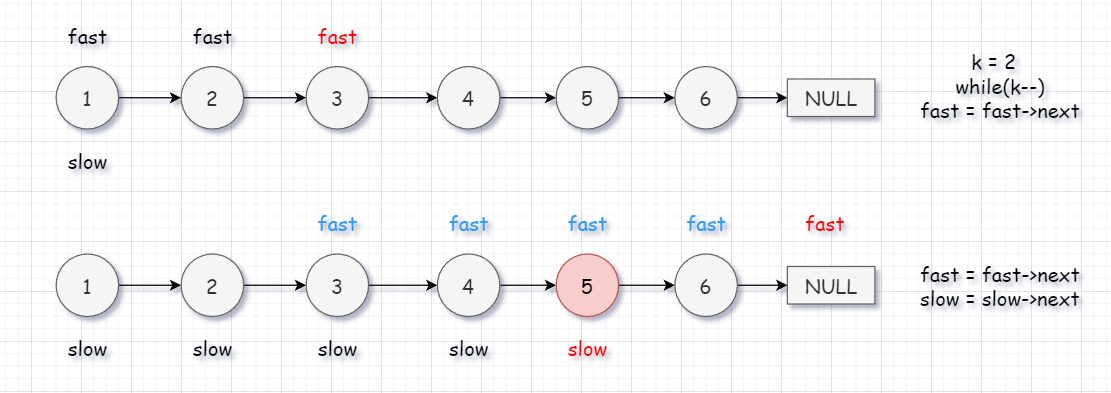
又是奇妙的快慢指针,这里大体是这样一个方案。
给定一个快指针 fast 和一个慢指针 slow。
我们要求链表倒数第 k 个节点,那么我们就先让快指针走 k 步。
然后让 fast 和 slow 一起走,当 fast 走到空指针,这时 slow 为倒数第 k 个节点。
注意:如果在 fast 走 k 步的过程中,fast 迭代为了空指针,这时直接返回空指针。
那么这里的原理是什么呢?
其实就是首先让 fast 走 k 步,让 fast 和 slow 的间隔为 k。链表的倒数第 k 个节点,就是正数 len + 1 - k 个节点,那么当我 fast 走到空指针后,链表走完,那么现在 fast 走的距离就相当于链表的长度 + 1,fast 和 slow的间隔为 k ,那么现在的 slow 就为正数 len + 1 - k个节点,这时返回 slow就是倒数第 k 个节点。
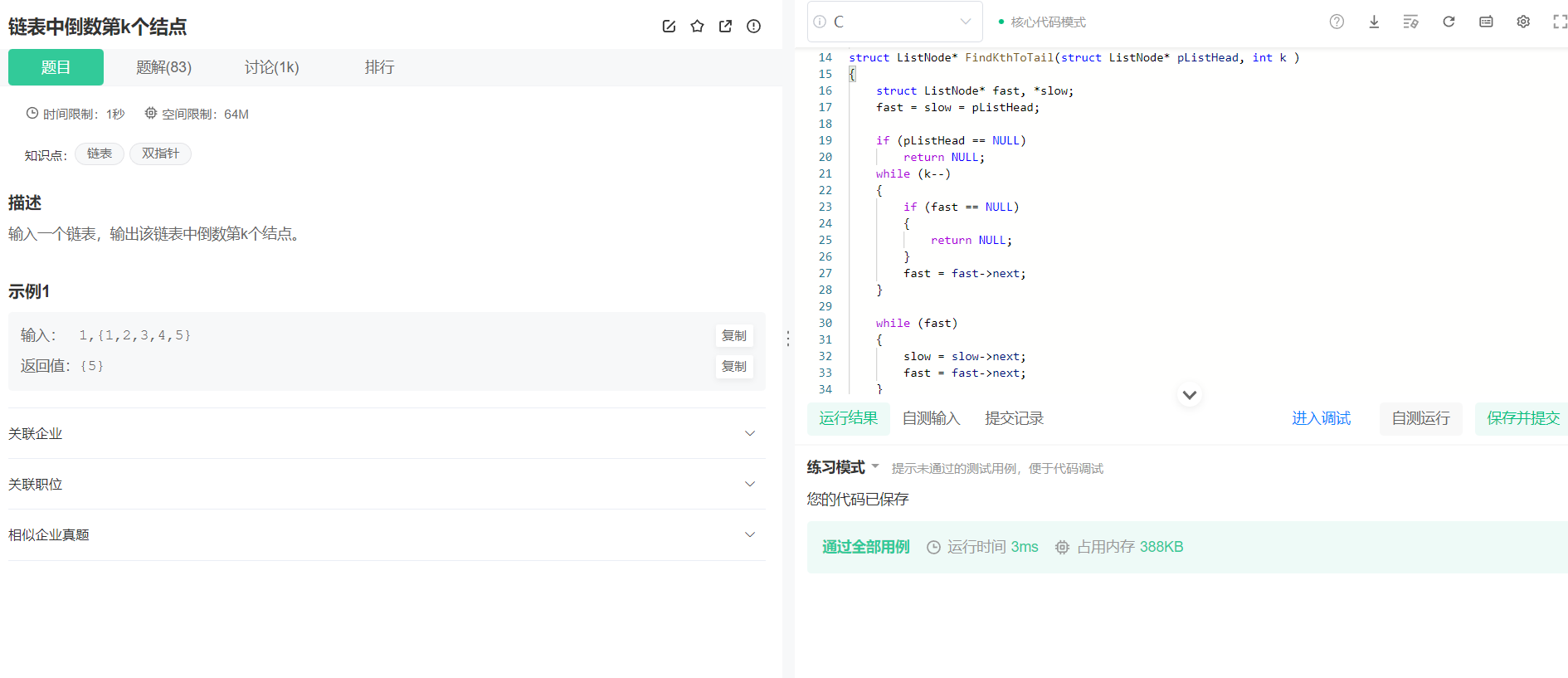
代码:
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{
struct ListNode* fast, *slow;
fast = slow = pListHead;
if (pListHead == NULL)
return NULL;
// fast 先走 k 步
while (k--)
{
// 放置 fast 先走到空
if (fast == NULL)
{
return NULL;
}
fast = fast->next;
}
// 迭代
while (fast)
{
slow = slow->next;
fast = fast->next;
}
return slow;
}
3. 链表分割
链接:CM11 链表分割
描述:
现有一链表的头指针 ListNode* pHead,给一定值x,编写一段代码将所有小于x的结点排在其余结点之前,且不能改变原来的数据顺序,返回重新排列后的链表的头指针。
思路:
题目要求我们将小于 x 的节点和大于等于 x 的节点分隔,小于 x 的节点在前,大于等于 x 的节点在后,且不能改变原来的数据顺序。
不能改变顺序就比较棘手,如果没有这个条件,我们可以用双指针来写。但是题目既然给出了要求,我们就得想办法解决。
我们创建一个新链表存放小于 x 的值,另一个存放大于等于 x 的值。然后遍历原链表,将符合条件的值放入对应的链表中,最后再将存放小于 x 的值的链表和存放大于等于 x 的值的链表链接起来。
那么这过程肯定是尾插,本题使用哨兵位是十分合适的,因为本题有很多的空指针处理的情况,所以我们设定两个哨兵位 lessHead 、 greaterHead。
再给定两个尾lessTail 、 greaterTail,用来尾插。 但是最后记得要释放哨兵位。
请注意,如果以 greaterHead 结束的元素不是链表的最后一个元素(即原链表最后一个元素小于 x ),就可能会造成 链表带环 的情况,需要断开环,然后将 greaterTail 的 next 置为空。同样的,过会也会画图来讲解。
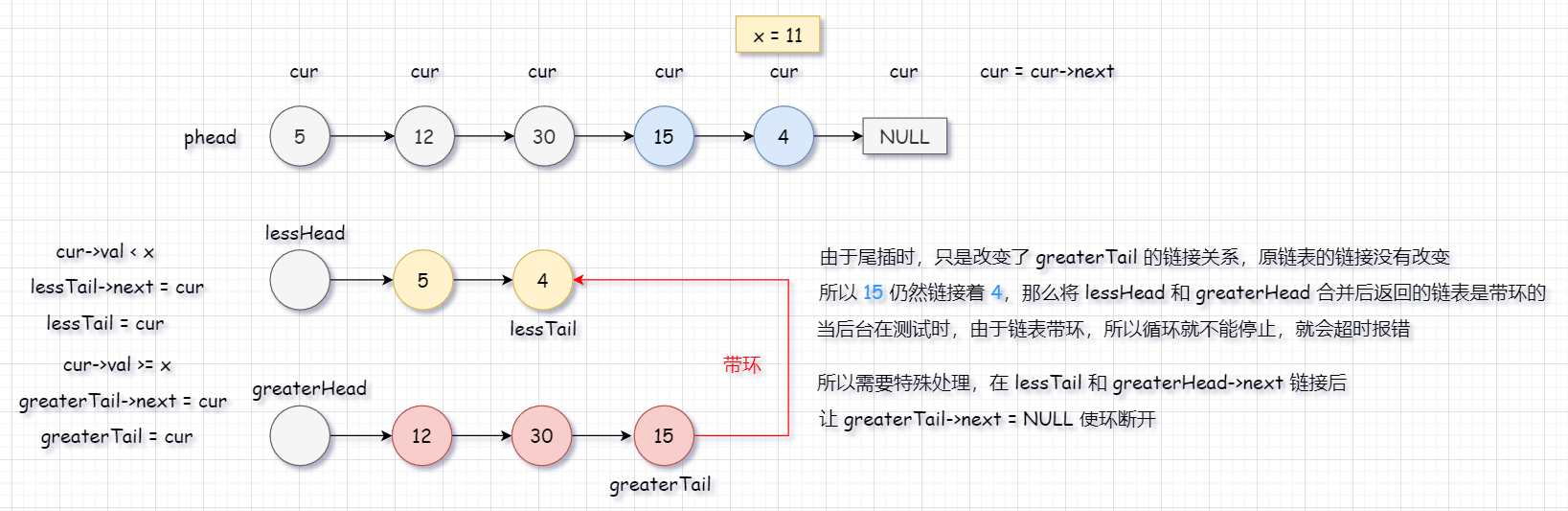
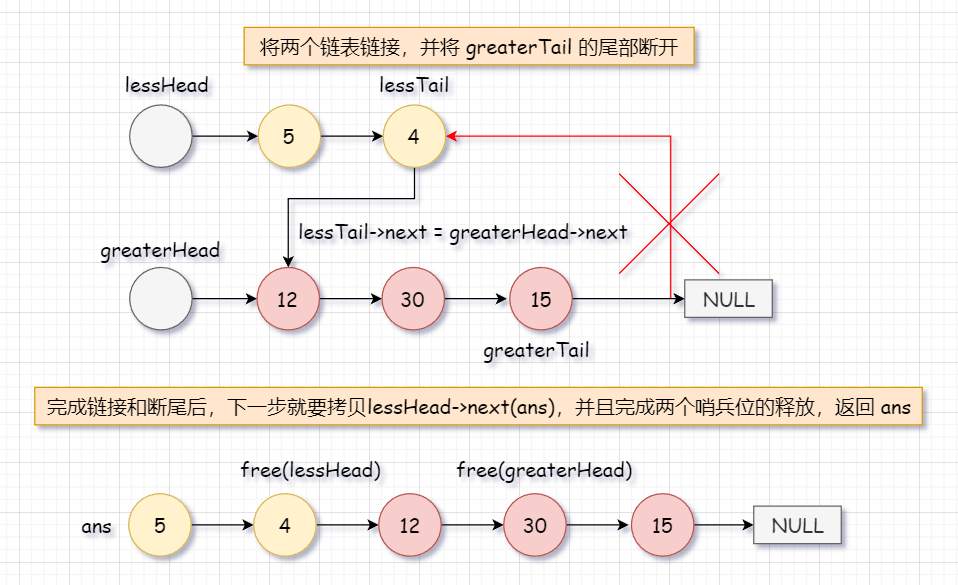
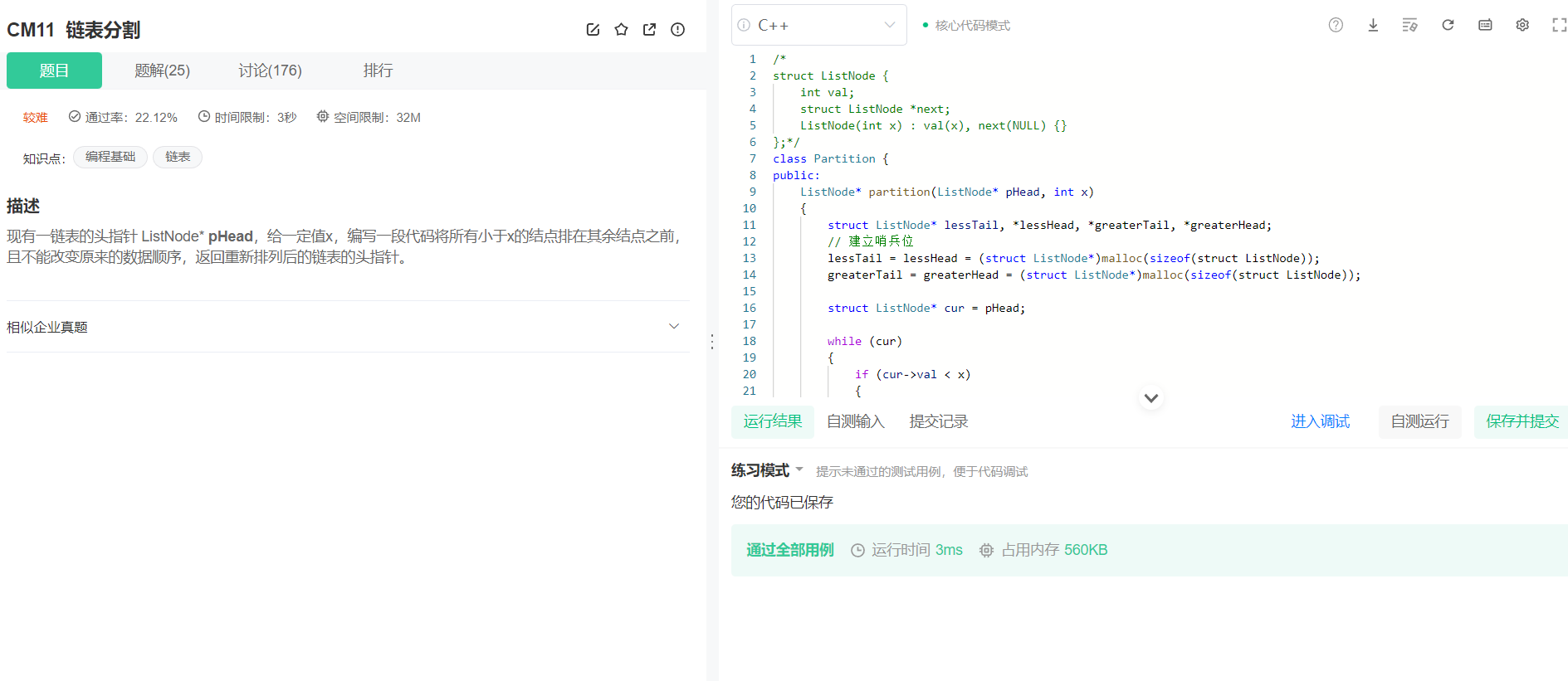
代码:
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};*/
class Partition {
public:
ListNode* partition(ListNode* pHead, int x)
{
struct ListNode* lessTail, *lessHead, *greaterTail, *greaterHead;
// 建立哨兵位
lessTail = lessHead = (struct ListNode*)malloc(sizeof(struct ListNode));
greaterTail = greaterHead = (struct ListNode*)malloc(sizeof(struct ListNode));
struct ListNode* cur = pHead;
while (cur)
{
if (cur->val < x)
{
lessTail->next = cur;
lessTail = cur;
}
else
{
greaterTail->next = cur;
greaterTail = cur;
}
cur = cur->next;
}
// 链接两个链表
lessTail->next = greaterHead->next;
greaterTail->next = NULL; // 断开环
// 拷贝节点,释放哨兵位
struct ListNode* ans = lessHead->next;
free(lessHead);
free(greaterHead);
return ans;
}
};
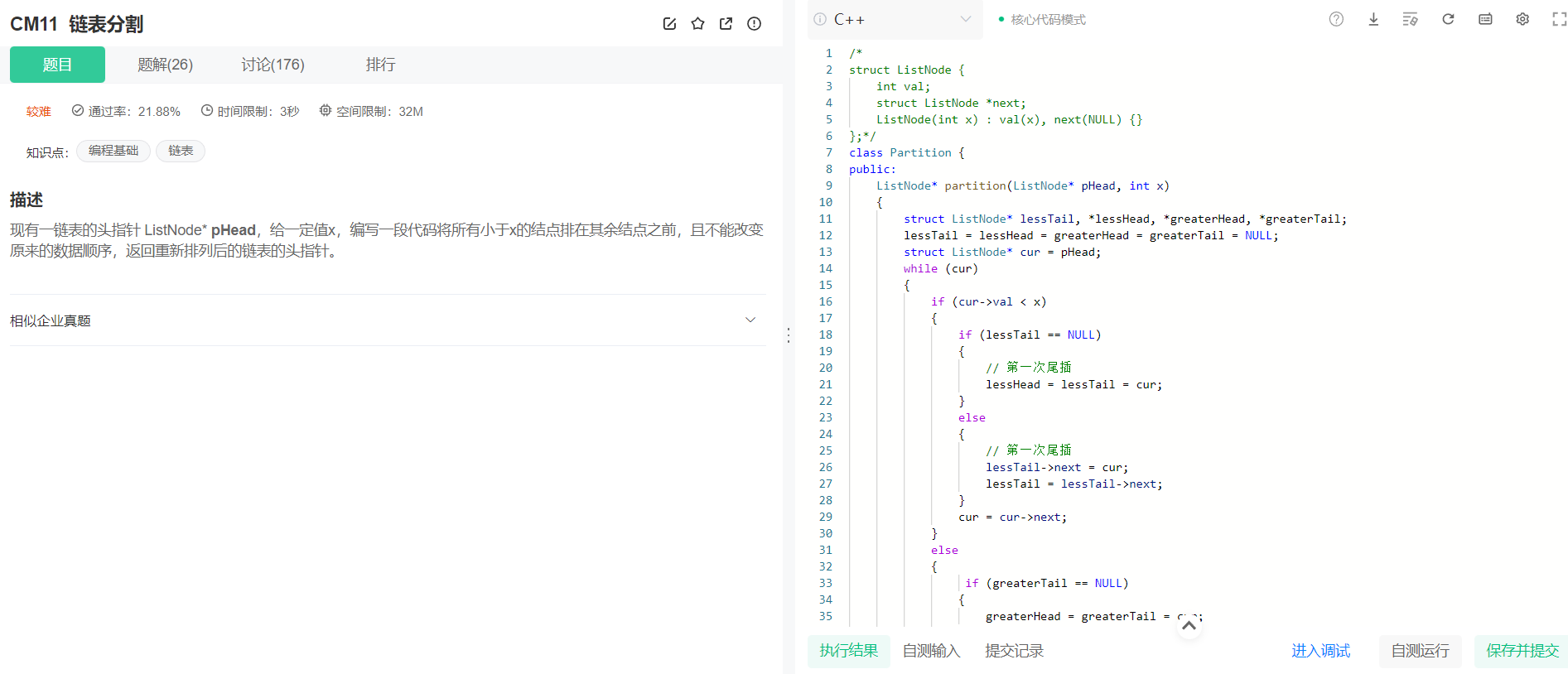
这道题目不用哨兵位也可以做,但是比较考验细节,思路大体差不多,有兴趣可以去试试,下面给出截图和代码:
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};*/
class Partition {
public:
ListNode* partition(ListNode* pHead, int x)
{
struct ListNode* lessTail, *lessHead, *greaterHead, *greaterTail;
lessTail = lessHead = greaterHead = greaterTail = NULL;
struct ListNode* cur = pHead;
while (cur)
{
if (cur->val < x)
{
if (lessTail == NULL)
{
// 第一次尾插
lessHead = lessTail = cur;
}
else
{
// 第一次尾插
lessTail->next = cur;
lessTail = lessTail->next;
}
cur = cur->next;
}
else
{
if (greaterTail == NULL)
{
greaterHead = greaterTail = cur;
}
else
{
greaterTail->next = cur;
greaterTail = greaterTail->next;
}
cur = cur->next;
}
}
// lessHead 为空,说明原链表为空或链表的值全大于 x
// 且链表尾部的 next 一定为空
// 返回 greaterHead
if (lessHead == NULL)
return greaterHead;
// 如果 lessHead 和 greaterHead 都不为空
// 说明正常分割
// 将其链接,greaterHead 尾部链空
if (lessHead != NULL && greaterHead != NULL)
{
lessTail->next = greaterHead;
greaterTail->next = NULL;
}
// 无论是正常分割,还是链表的值全小于 x
// 都是返回 lessHead
return lessHead;
}
};
4. 链表的回文结构
链接:OR36 链表的回文结构
描述:
对于一个链表,请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法,判断其是否为回文结构。
给定一个链表的头指针A,请返回一个bool值,代表其是否为回文结构。保证链表长度小于等于900。
示例:
测试样例:1->2->2->1
返回:true
思路:
如果不加空间复杂度为O(1)的限制的话,那么我们可以创建一个数组,然后遍历链表,将链表中元素放到数组中,从数组前后开始遍历,判断是否是回文结构。
但是这里已经给定了要求,那我们便最好不要使用这种写法,所以我们要重新设计一个方法。
我们仔细想想,链表的回文结构,不就是从头开始向后遍历的元素和从后向前遍历的元素遍历到中间位置相等吗?
那么我们找到中间节点 mid,然后将 mid 开始的链表反转,将这个链表的起始节点给定为 reHead。然后奇偶情况遍历链表不就可以了吗?接下来我们展开讨论:
我们假定 reHead 已经反转,给定 curR来遍历 reHead,给定 curA 遍历 原链表 。
原链表为奇数个节点:curA、curR 同时开始走, reHead 先走完,当 curA 走到 reHead 的 前一个节点 时,并不会走到 rehead 。因为原链表的结构并没有改变,所以会走到原链表的下一个位置。所以不用担心 reHead 反转后链表表面上改变,而导致回文结构辨识不出的情况。(这样说可能有些模糊,但是没关系,马上有图解)
原链表为偶数个节点:curA、curR同时开始走,reHead先走完。这里由于 reHead 前和从 reHead 开始的节点个数相等,所以也就不需要想那么多。
结论:无论奇数偶数,只要 curA 和 curR 中有一个走到空就停止。
所以我们可以归纳一下这里的步骤:找中心节点 -> 反转中心节点开始的链表 -> 迭代判断。
而这里非常巧的是,我们上篇博客中已经写过了前两步——链表的中心节点、反转链表,所以到时候直接搬运即可~
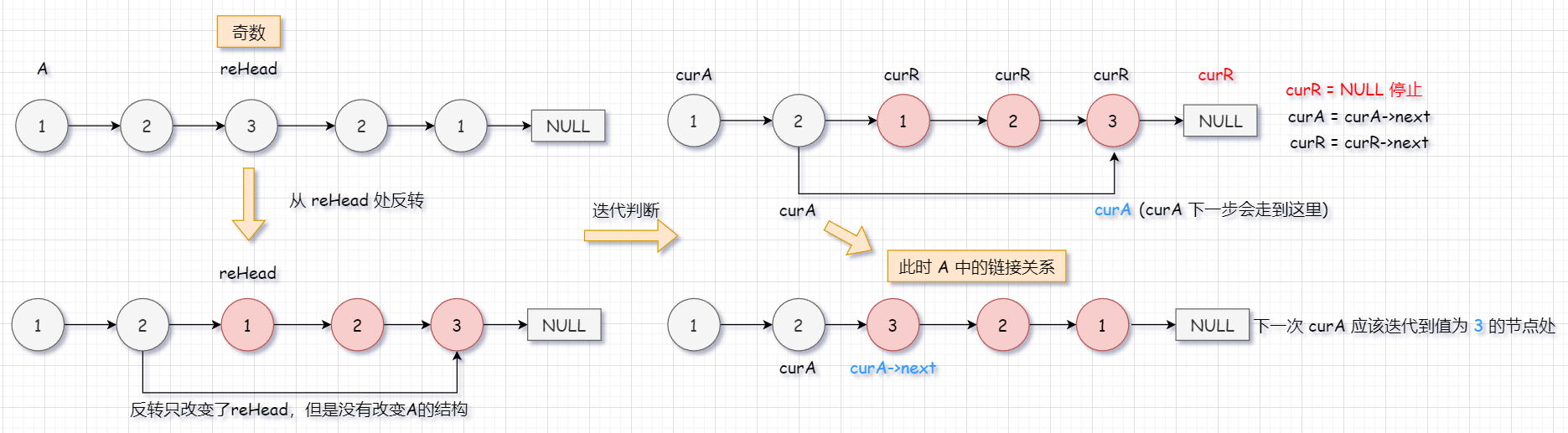
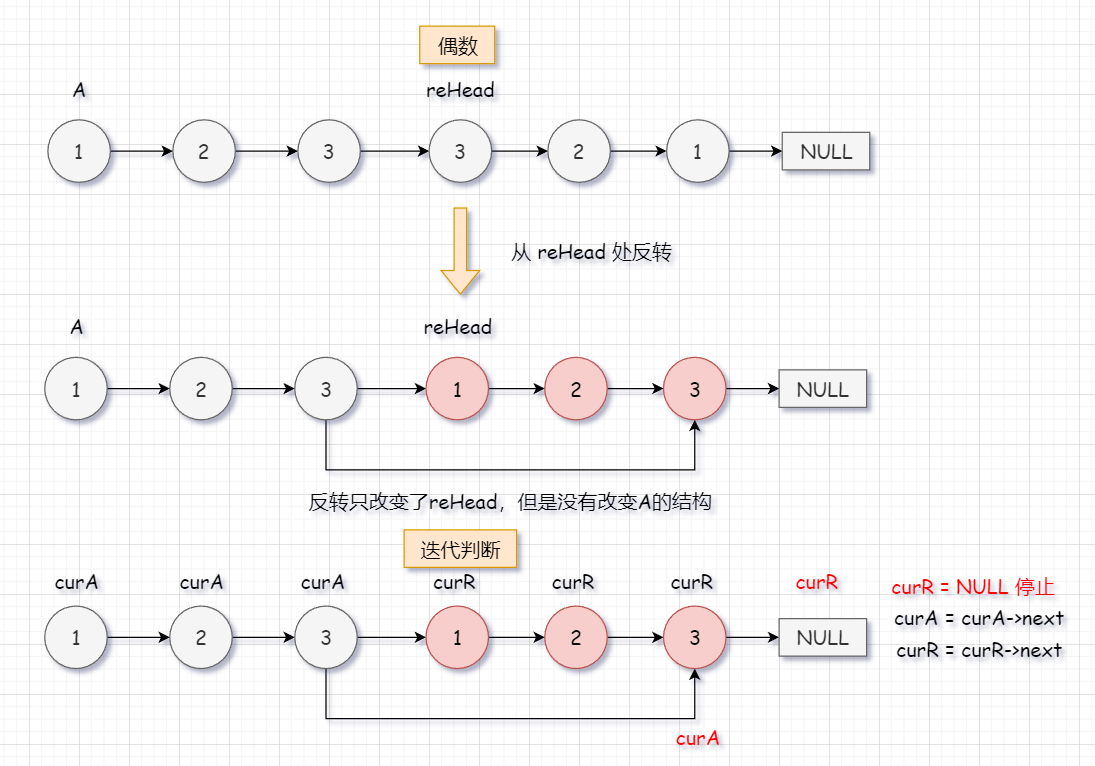

注:C++兼容C的语法,所以用C的语法写完全可以。而且这道题目在力扣上没有限制空间复杂度,所以采用牛客网的~
代码:
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};*/
struct ListNode* middleNode(struct ListNode* head)
{
struct ListNode* fast, *slow;
fast = slow = head;
while (fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
struct ListNode* reverseList(struct ListNode* head)
{
struct ListNode* cur = head;
struct ListNode* newNode = NULL;
while (cur)
{
struct ListNode* next = cur->next;
// 头插
cur->next = newNode;
newNode = cur;
// cur迭代
cur = next;
}
return newNode;
}
class PalindromeList {
public:
bool chkPalindrome(ListNode* A) {
struct ListNode* mid = middleNode(A);
struct ListNode* rHead = reverseList(mid);
// A和rHead一般不会直接使用,拷贝一份
struct ListNode* curA = A;
struct ListNode* curR = rHead;
while (curA && curR)
{
if (curA->val != curR->val)
{
return false;
}
curA = curA->next;
curR = curR->next;
}
return true;
}
};
5. 相交链表
链接:160. 相交链表
描述:
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
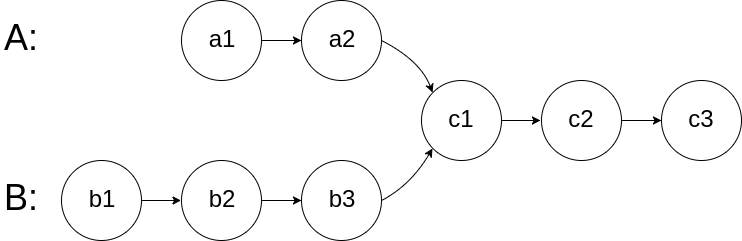
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal- 相交的起始节点的值。如果不存在相交节点,这一值为0listA- 第一个链表listB- 第二个链表skipA- 在listA中(从头节点开始)跳到交叉节点的节点数skipB- 在listB中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点headA和headB传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例1:
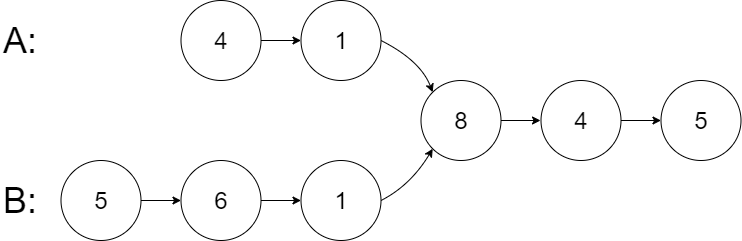
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at ‘8’
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例2:
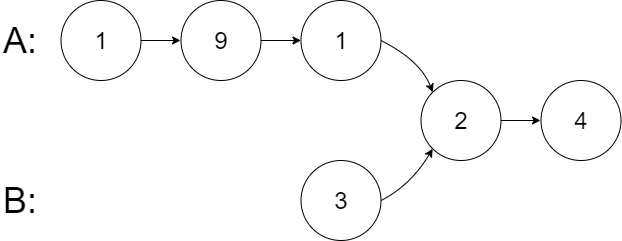
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at ‘2’
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例3:
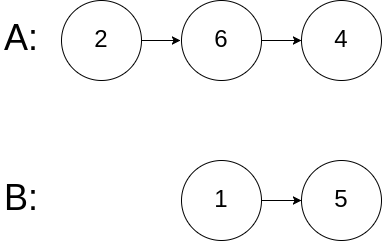
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA中节点数目为mlistB中节点数目为n1 <= m, n <= 3 * 10^41 <= Node.val <= 10^50 <= skipA <= m0 <= skipB <= n- 如果
listA和listB没有交点,intersectVal为0 - 如果
listA和listB有交点,intersectVal == listA[skipA] == listB[skipB]
思路1:
如果要说这道题目,如果不考虑任何方法,那么就直接 暴力求解 。
取其中一条链表,让它的所有节点和另一条链表的所有元素比较。判断是否有交点,有则返回该节点;链表遍历完没有交点的话,返回空指针。
而且这次也出奇的巧,暴力求解在力扣上也能跑过~
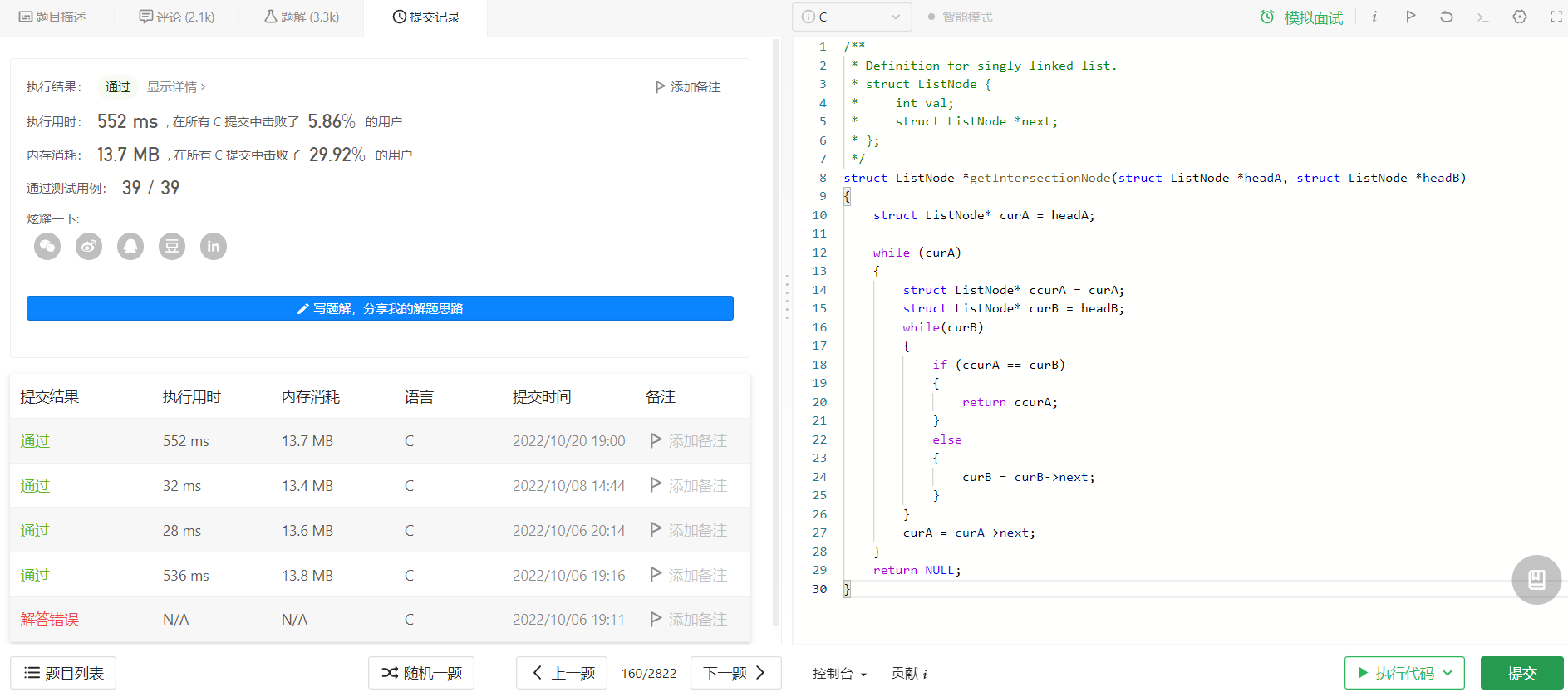
但是在速度方面就很难看了,那我们能不能做出一些优化?看思路2↓
思路2(精讲):
首先,我们要明确的一点是,只要两条链表 有交点 ,那么这两条链表的 尾结点 就是相等的。
因为单链表中存储的一部分是数据,一部分是下一个节点的地址,一个节点中只有一个 next ,所以以后链表走的都是一条路。
就像这样:
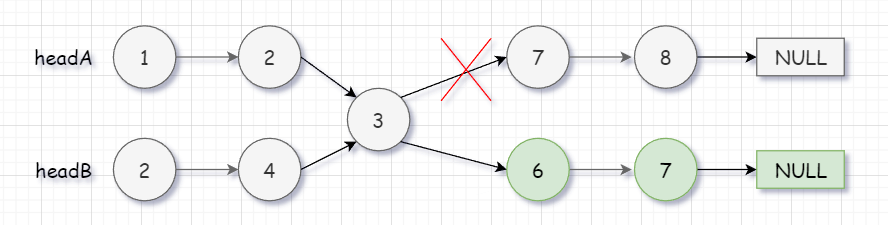
所以如果两个链表相交,就说明它们的 尾结点 肯定相同,那么遍历两条链表,比较它们的尾。
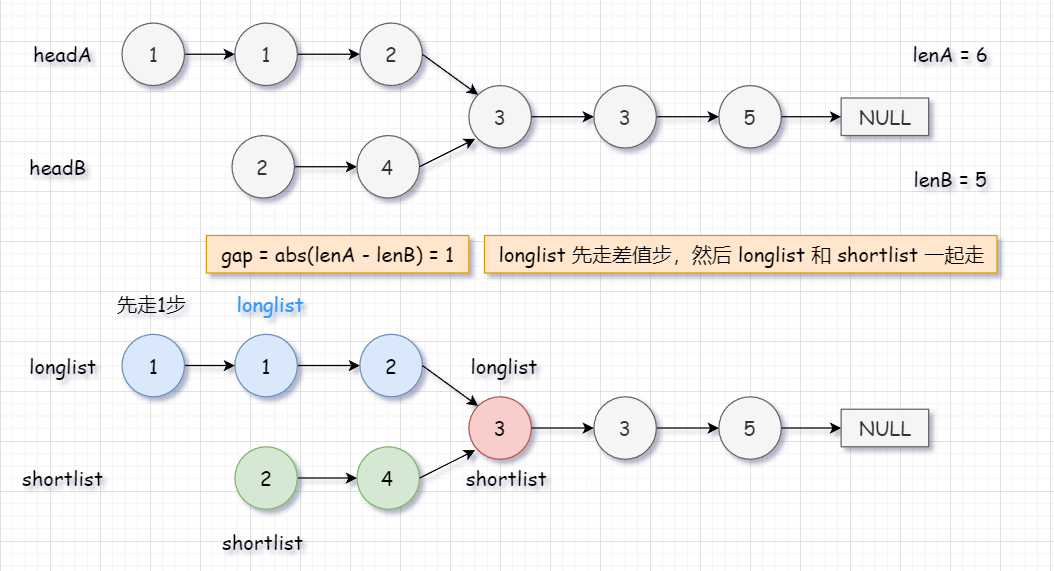
然后算出两条链表的长度,让长的链表走差值步。
那么让我长链表先走差值步,走到和短链表一样长,然后一起走,肯定就能找到交点了呀!找到交点后返回长链表、短链表节点中的任意一个。
注意点(已踩坑):
当我们求长链表和短链表时,如果使用了三目操作符,比如:
struct ListNode* longList = lenA > lenB ? headA : headB;
struct ListNode* shortList = lenA < lenB ? headA : headB;
如果这样写,大多测试用例都能跑过,但是如果碰上一组两条链表的值相等的情况:
相交点 intersectVal:4
headA:②→③→④→⑤
headB:②→③→④→⑤
这样那么 longList 和 shortList 都是 headB,那么求相交点时,就直接返回第一个节点②了。
所以要控制 条件相同 ,让 longList 和 shortList 为不同的链表。
比如这样:
struct ListNode* longList = lenA > lenB ? headA : headB;
struct ListNode* shortList = lenA > lenB ? headB : headA;
注:可能是因为博主太菜,在这道题目 n 刷时,突然这么写了,找了半天没发现错误…希望大家不要踩坑…
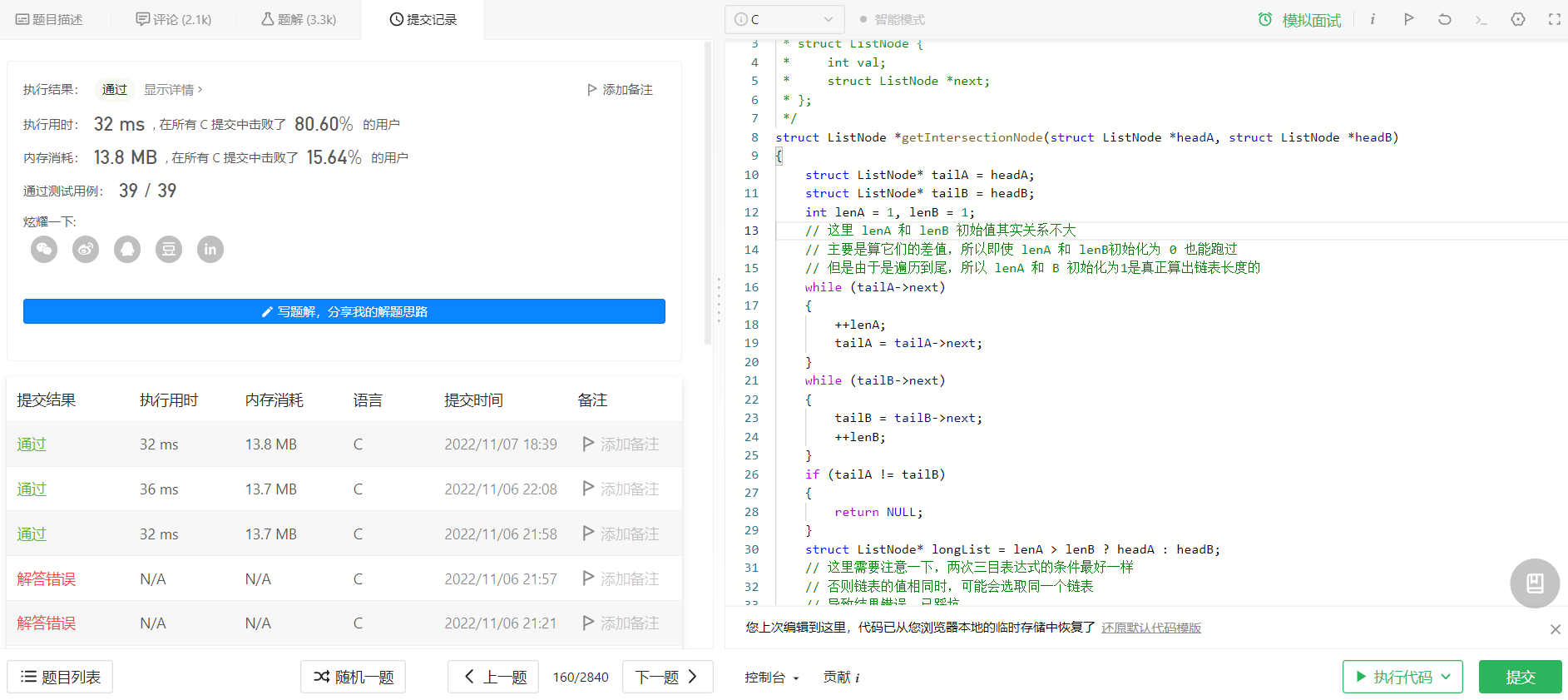
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
struct ListNode* tailA = headA;
struct ListNode* tailB = headB;
int lenA = 1, lenB = 1;
// 这里 lenA 和 lenB 初始值其实关系不大
// 主要是算它们的差值,所以即使 lenA 和 lenB初始化为 0 也能跑过
// 但是由于是遍历到尾,所以 lenA 和 B 初始化为1是真正算出链表长度的
while (tailA->next)
{
++lenA;
tailA = tailA->next;
}
while (tailB->next)
{
tailB = tailB->next;
++lenB;
}
if (tailA != tailB)
{
return NULL;
}
struct ListNode* longList = lenA > lenB ? headA : headB;
// 这里需要注意一下,两次三目表达式的条件最好一样
// 否则链表的值相同时,可能会选取同一个链表
// 导致结果错误,已踩坑
struct ListNode* shortList = lenA > lenB ? headB : headA;
int gap = abs(lenA - lenB);// 求差值
while (gap--)
{
longList = longList->next;
}
while (longList != shortList)
{
longList = longList->next;
shortList = shortList->next;
}
return longList;
}
6. 结语
到这里本篇博客就到此结束了,这次的题目还是比较麻烦的,如果没完全理解可以画画图,多看看,多写写。
在下期,我依旧会为大家来带链表的OJ题,但是形式会和前两篇不太一样,我会用小剧场的形式,帮助大家在互动中带大家吃透链表中经典的问题!剧透一下,下一期内容会很精彩!我们敬请期待~
如果觉得anduin写的还不错的话,还请一键三连!如有错误,还请指正!
我是anduin,一名C语言初学者,我们下期见!



![[附源码]计算机毕业设计JAVAjsp宠物店管理系统](https://img-blog.csdnimg.cn/05c3c66aaca14031bb84bf237a8aa2f1.png)
![Mybatis-Plus知识点[MyBatis+MyBatis-Plus的基础运用]](https://img-blog.csdnimg.cn/bd4fe645a435422b8fd6b4cd9969466f.png)