目录
一.概念
二.跟二叉树的联系
前序遍历(先根遍历)
中序遍历(中根遍历)
后序遍历(后根遍历)
二叉树例题
三.知二求一并还原二叉树
已知前序遍历和中序遍历
例题
解答
已知中序遍历和后序遍历
例题
解答
注意
一.概念
- 前缀表达式:前缀表达式的运算符位于两个相应操作数之前,前缀表达式又被称为前缀记法或波兰式。
- 中缀表达式:中缀表达式是一种通用的算术或逻辑公式表示方法,操作符以中缀形式处于操作数的中间。中缀表达式是人们常用的算术表示方法。
- 后缀表达式:后缀表达式与前缀表达式类似,只是运算符位于两个相应操作数之后,后缀表达式也被称为后缀记法或逆波兰式。

前缀、中缀、后缀表达式是对表达式的不同记法,其区别在于运算符相对于操作数的位置不同,前缀表达式的运算符位于操作数之前,中缀和后缀同理
虽然人的大脑很容易理解与分析中缀表达式,但对计算机来说中缀表达式却是很复杂的,因此计算表达式的值时,通常需要先将中缀表达式转换为前缀或后缀表达式,然后再进行求值。对计算机来说,计算前缀或后缀表达式的值非常简单。
二.跟二叉树的联系
- 前缀表达式对应于二叉树的前序遍历
- 中缀表达式对应于二叉树的中序遍历
- 后缀表达式对应于二叉树的后序遍历
前序遍历(先根遍历)
访问根结点的操作发生在遍历其左右子树之前(根->左->右)。
中序遍历(中根遍历)
访问根结点的操作发生在遍历其左右子树之中(左->根->右)。
后序遍历(后根遍历)
访问根结点的操作发生在遍历其左右子树之后(左->右->根)。
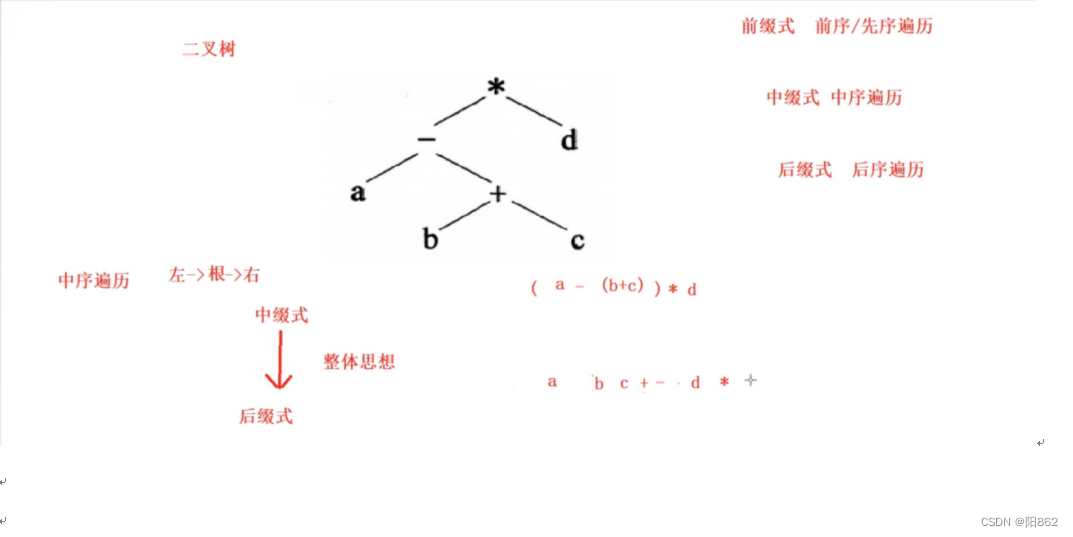
二叉树例题
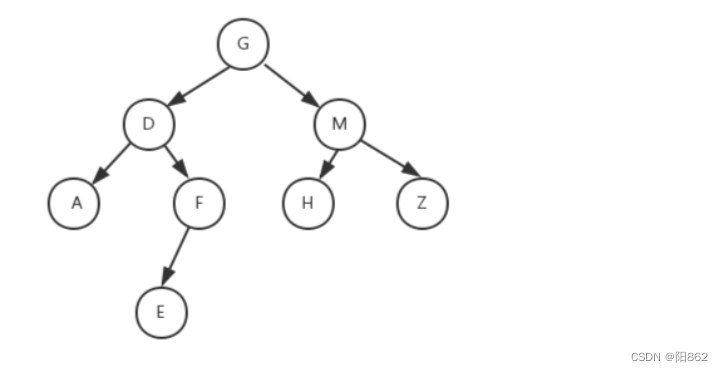
前序遍历(根左右):GDAFEMHZ
中序遍历(左根右):ADEFGHMZ
后序遍历(左右根):AEFDHZMG
三.知二求一并还原二叉树
已知前序遍历和中序遍历
例题
例如输入前序遍历序列{1,2,4,7,3.5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},重建二叉树并返回后序遍历序列
解答
只要牢记概念,前序遍历是指先根再左右;中序遍历是指先左再根右。
所以可得1是根,那么4,7,2就是1的左子树;5,3,8,6就是1的右子树;然后再从4,7,2里找可得2是根,4、7是根的左子树,再4是根,然后就可知道7是4的右子树,后面的5,3,8,6同理可得。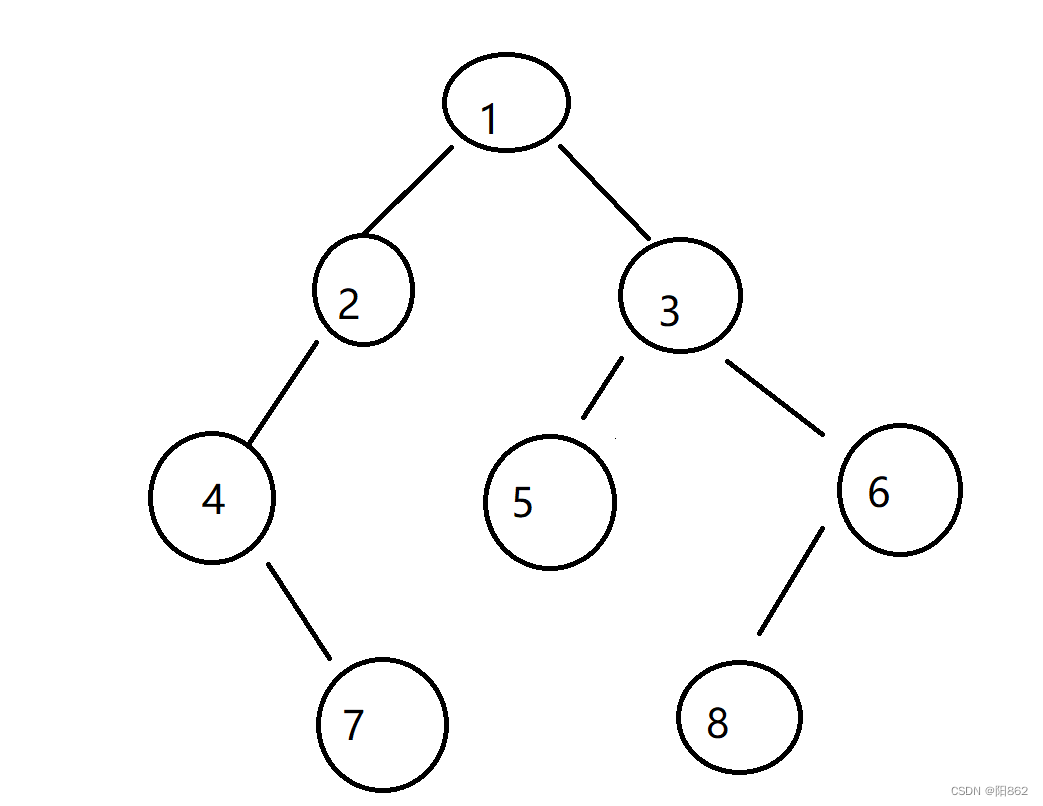
所以后序遍历是:7 4 2 5 8 6 3 1
已知中序遍历和后序遍历
例题
已知中序遍历:HDMIBJNEAFKCG.后序遍历:HMIDNJEBKFGCA.求出此二叉树Q。
解答
跟上面那个题目本质是一样的,只要牢记概念,中序遍历是指先左再根右。后序遍历是先左右后根。
所以可先得A为根,HDMIBJNE是它的左子树,FKCG是它的右子树;我们先只看左子树HDMIBJNE,再从后序遍历里查看,可得B是根,HDMI是它的左子树,JNE是它的右子树;继续可得D是根,H是它的左子树,MI是它的右子树;可得I是根,M是它的左子树;后面的右子树同理就可得。
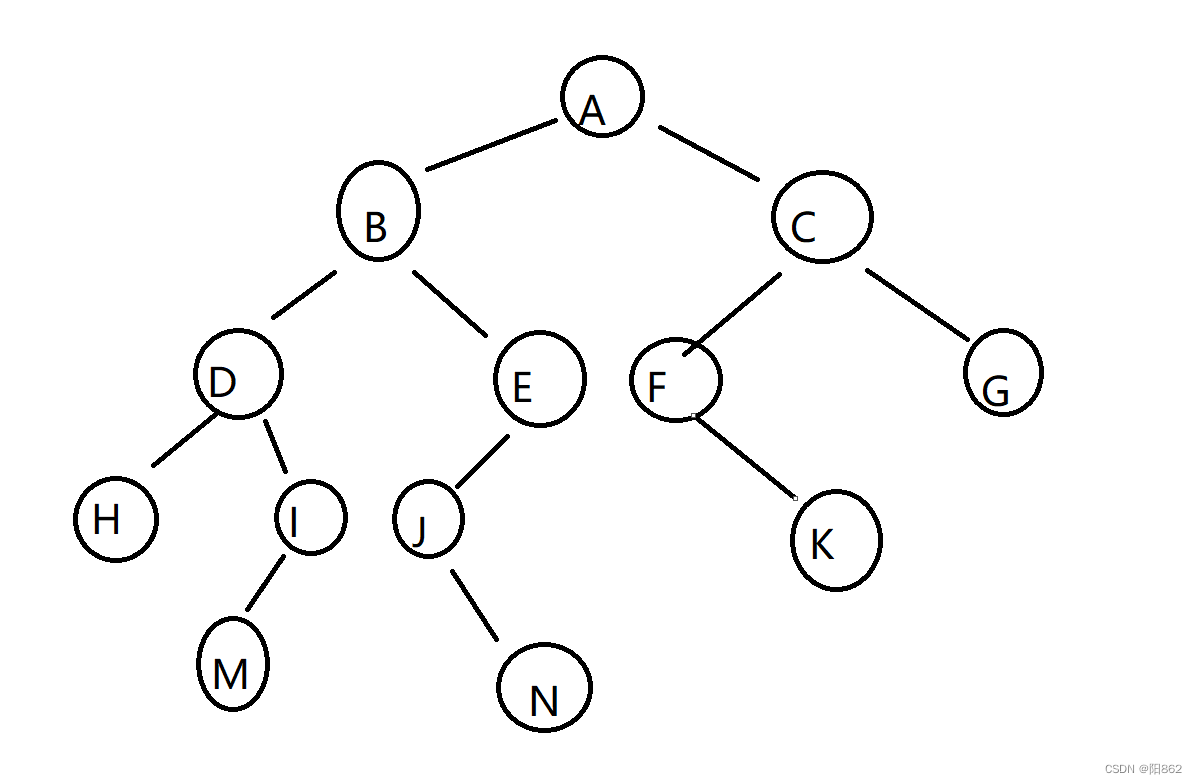
所以前序遍历是:A B D H I M E J N C F K G
注意
如果是知道前序遍历和后续遍历,是无法确定唯一的二叉树的!