今天继续学习动规解决相关问题。
337.打家劫舍|||
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:
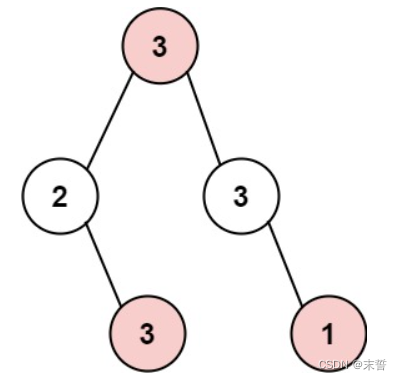
输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
思路:
1.本题是第一次接触动规与二叉树结合起来的题目,一开始确实没什么思路。最初想到完全用递归二叉树的方式来做,但最后很不幸超时了。
2.尽管纯递归超时了,但既然本题是二叉树那就一定涉及到递归。在通过观看讲解视频后发现,纯递归的方法会有多次重复的运算做了无用功,且一直都是实时运算的,因此考虑使用动规的方法来解决。
3.既然选择要用动规,那么dp数组如何确定呢?本题需要存储每一个结点取或者不取的情况,因此我们为每一个结点创建一个dp数组用于存储当前结点取或不取的情况,因此dp数组长度为2,我们规定dp[0]为不取当前结点的最大金额,dp[1]为取当前结点的最大金额。
4.然后我们按照递归的思路来想一想递归的顺序,本题如果从根节点从上往下进行遍历,一开始考虑取或不取就会比较复杂,因此我们选择后序遍历,从叶子结点开始向上逐步递归会更加简单,而且当前结点取或不取,其取值实际上也受到下面的孩子节点的影响。
5.然后关于递推公式,如果当前结点取,那么首先要加上当前结点的值,然后加上不取左右孩子的情况下左右孩子各自的最大金额;如果当前结点不取,那么直接等于左右孩子取或不取的最大值之和。(这里可能有点抽象,建议配合代码观看)
class Solution {
public:
//dp数组就是长度为2的返回值,dp[0]代表不取当前结点的最大金额,dp[1]代表取当前结点的最大金额
vector<int> robTree(TreeNode* cur){
//空结点直接返回[0,0]
if(cur == nullptr) return vector<int>{0,0};
vector<int> leftRob = robTree(cur->left);//左
vector<int> rightRob = robTree(cur->right);//右
//中
int val1 = cur->val + leftRob[0] + rightRob[0];//取当前结点的最大金额
int val2 = max(leftRob[0], leftRob[1]) + max(rightRob[0], rightRob[1]);//不取当前结点的最大值
return vector<int>{val2, val1};
}
int rob(TreeNode* root) {
vector<int> result = robTree(root);
return max(result[0], result[1]);
}
};启发:
1.本题作为初次接触二叉树融合动规的题目,给人一种无从下手的感觉,因为Day50的打家劫舍|和打家劫舍||实则都是转化为相对简单的线性结构来解决,但本题数据结构为二叉树,必须得通过递归的方式来遍历二叉树,而其中涉及到动规最难想的主要还是dp数组是什么及其含义,本题为了避免重复计算确实需要一个容器来存储我们中途运算的结果,而本题的dp数组就当仁不让充当了这样的一种容器,因此dp数组长度为2且每个节点都有一个自己的dp数组对应其取或不取的情况。