gitee代码:https://gitee.com/WangZihao64/data-structure-and-algorithm/tree/master/BST
一、概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
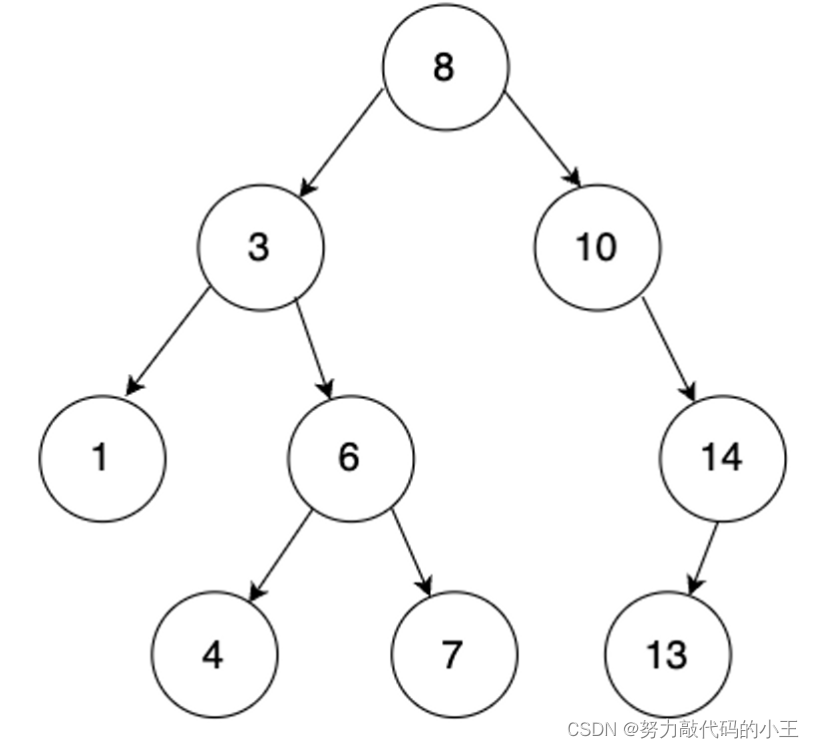
二、查找
从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找
最多查找高度次,走到到空,还没找到,这个值不存在
bool Find(const K& val)
{
Node* cur=_root;
while(cur)
{
if(cur->_val>val)
{
cur=cur->_left;
}
else if(cur->_val<val)
{
cur=cur->_right;
}
else
{
return true;
}
}
return false;
}
三、插入
树为空,则直接新增节点,赋值给root指针
树不空,按二叉搜索树性质查找插入位置,插入新节点
//插入可能失败,因为我们不能插入相同的值
bool Insert(const K& val)
{
//头插
if(_root== nullptr)
{
_root=new Node(val);
return true;
}
Node* cur=_root;
//左子树所有值小于其根节点的值
//右子树所有值大于其根节点的值
//记录前一个节点
Node* prev= nullptr;
while(cur)
{
if(cur->_val<val)
{
prev=cur;
cur=cur->_right;
}
else if(cur->_val>val)
{
prev=cur;
cur=cur->_left;
}
//值相同
else
{
return false;
}
}
cur=new Node(val);
if(val>prev->_val)
{
prev->_right=cur;
}
else
{
prev->_left=cur;
}
return true;
}
四、删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情
况:
1.要删除的结点无孩子结点
2.要删除的结点只有左孩子结点
3.要删除的结点只有右孩子结点
4.要删除的结点有左、右孩子结点
在处理上我们的情况1可以和情况2,3合并起来,所以这里着重理解2,3,4这三种情况
首先第2种情况我们可以看作删除14
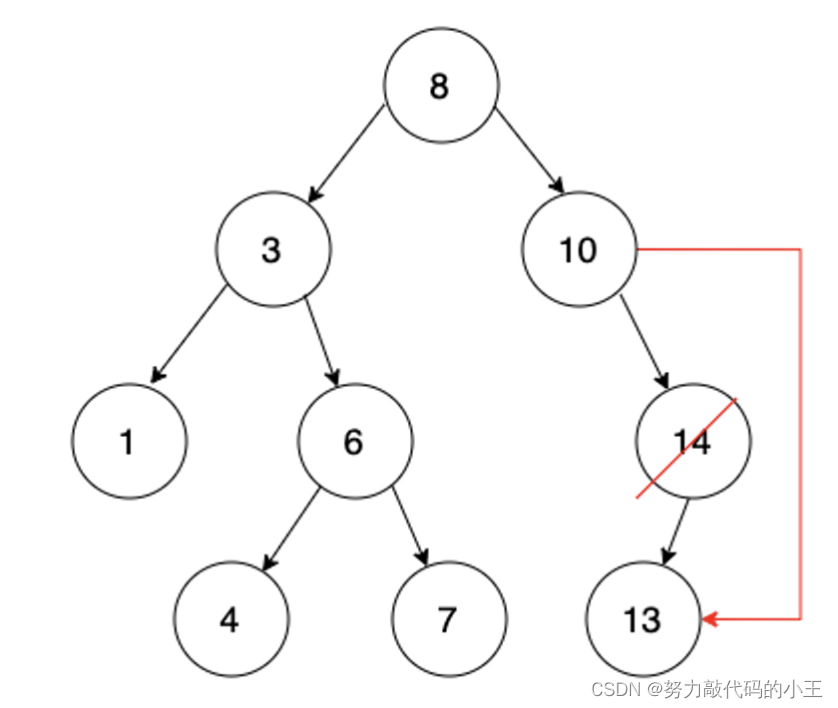
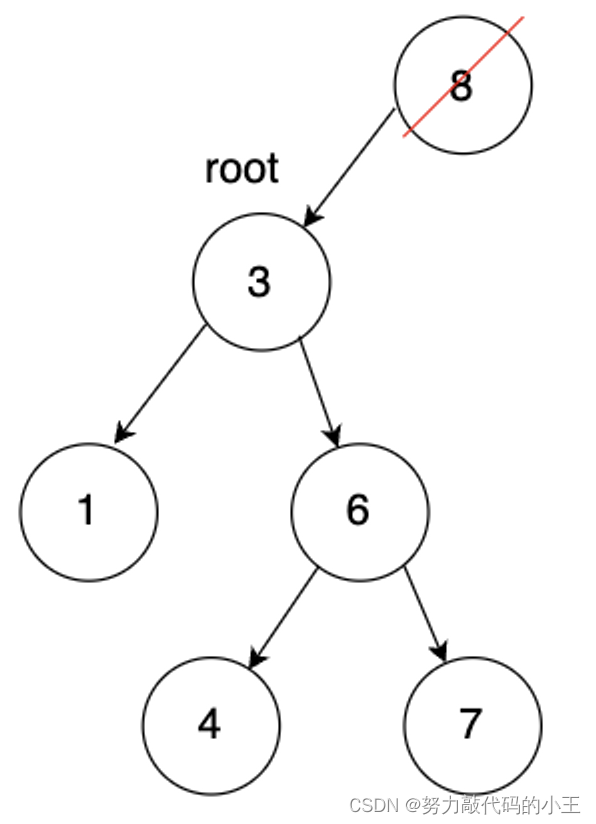
14这个结点只有左孩子,我们只需要让10这个结点的右孩子指向14的左孩子即可,第3种情况的处理方法和第2种是一样的(也包括第一种),如果是这样的一棵树,并且我们需要删除头节点,就需要单独处理
bool Erase(const K& val)
{
Node* cur=_root;
Node* parent=_root;
while(cur)
{
if(cur->_val>val)
{
parent=cur;
cur=cur->_left;
}
else if(cur->_val<val)
{
parent=cur;
cur=cur->_right;
}
//找到了对应的value
else
{
//有一个为空,如果是根节点需要单独处理
if(cur->_left== nullptr)
{
if(_root==cur)
{
_root=cur->_right;
}
else
{
if(parent->_left==cur)
{
parent->_left=cur->_right;
}
else
{
parent->_right=cur->_right;
}
}
delete cur;
}
else if(cur->_right== nullptr)
{
if(_root==cur)
{
_root=cur->_left;
}
else
{
if(parent->_left==cur)
{
parent->_left=cur->_left;
}
else
{
parent->_right=cur->_left;
}
}
delete cur;
}
//左右都不为空,下面处理
else
{
}
return true;
}
}
return false;
}
情况4(左右结点都不为空)
我们需要找左子树的最大结点或者找右子树的最小结点(这里找右子树的最小结点)
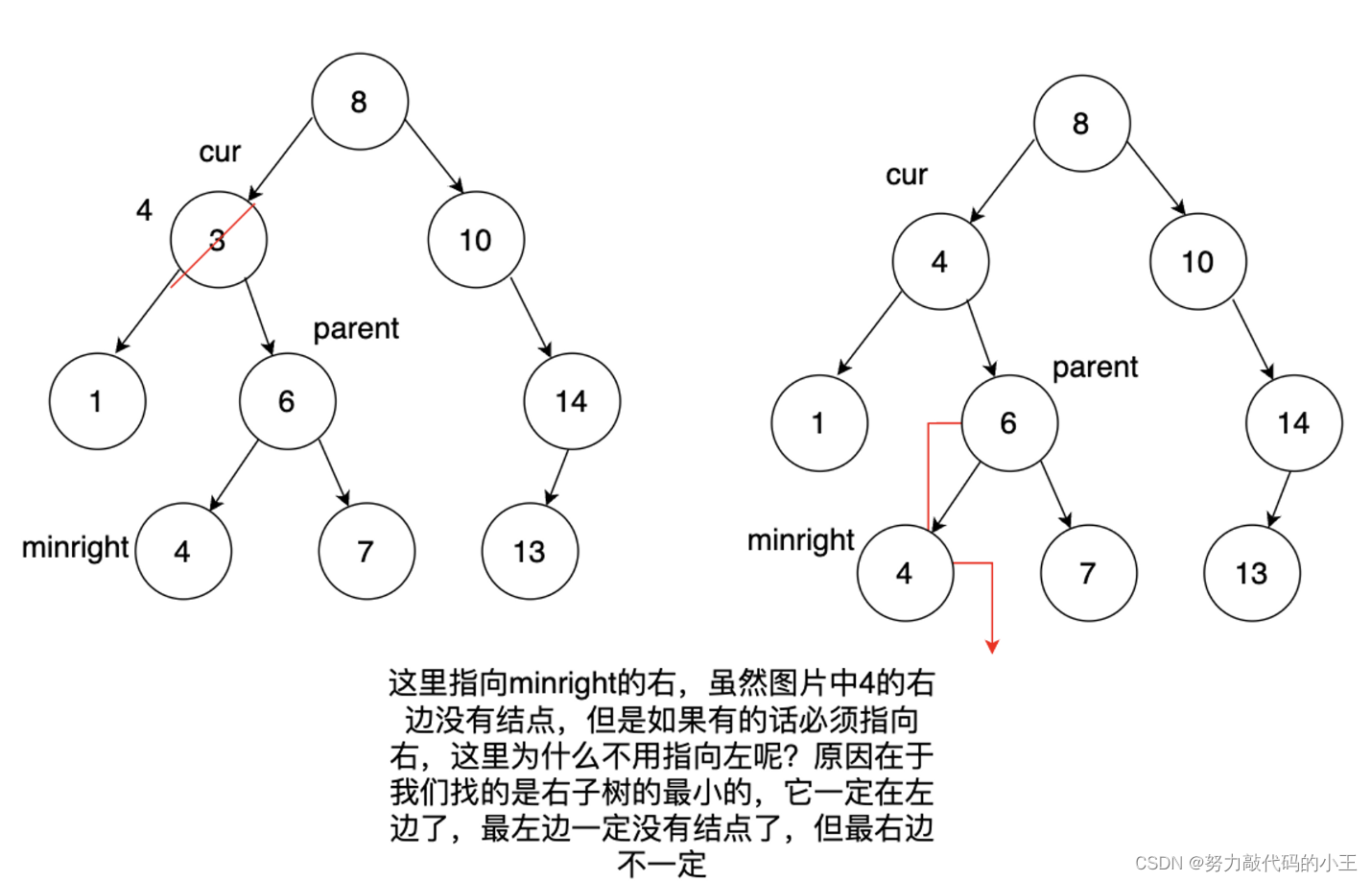
/2种方案: 1.左子树中找最大的,即找到左子树然后一直向右查找(因为右子树一定比根大)
//2.右子树中找最小的,即找到右子树然后一直向左查找(因为左子树一定比根小)
//这里采用从右子树中找最小的
Node* minright=cur->_right;
Node* prev=cur;
while(minright->_left)
{
prev=minright;
minright=minright->_left;
}
swap(cur->_val,minright->_val);
if(prev->_left==minright)
{
prev->_left=minright->_right;
}
else
{
prev->_right=minright->_right;
}
delete minright;