要点:
- 手写数字识别用简单的线性进行分类效果比较差,添加卷积层和池化层效果会相对较好。
参考文档:百度官方文档
一 网络结构
前几节我们尝试使用与房价预测相同的简单神经网络解决手写数字识别问题,但是效果并不理想。原因是手写数字识别的输入是28 × 28的像素值,输出是0-9的数字标签,而线性回归模型无法捕捉二维图像数据中蕴含的复杂信息,如 图1 所示。无论是牛顿第二定律任务,还是房价预测任务,输入特征和输出预测值之间的关系均可以使用“直线”刻画(使用线性方程来表达)。但手写数字识别任务的输入像素和输出数字标签之间的关系显然不是线性的,甚至这个关系复杂到我们靠人脑难以直观理解的程度。
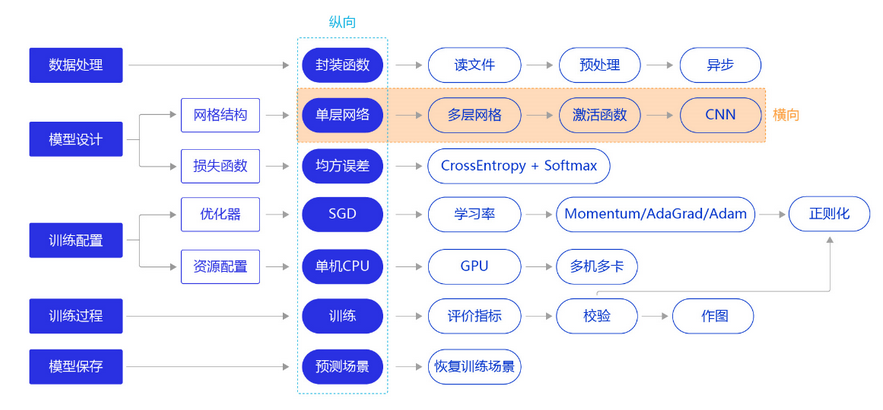
因此,我们需要尝试使用其他更复杂、更强大的网络来构建手写数字识别任务,观察一下训练效果,即将“横纵式”教学法从横向展开,如 图2 所示。本节主要介绍两种常见的网络结构:经典的多层全连接神经网络和卷积神经网络。
1 数据处理
在介绍网络结构前,需要先进行数据处理,代码与上一节保持一致。
#数据处理部分之前的代码,保持不变
import os
import random
import paddle
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
import gzip
import json
# 定义数据集读取器
def load_data(mode='train'):
# 加载数据
datafile = './work/mnist.json.gz'
print('loading mnist dataset from {} ......'.format(datafile))
data = json.load(gzip.open(datafile))
print('mnist dataset load done')
# 读取到的数据区分训练集,验证集,测试集
train_set, val_set, eval_set = data
# 数据集相关参数,图片高度IMG_ROWS, 图片宽度IMG_COLS
IMG_ROWS = 28
IMG_COLS = 28
if mode == 'train':
# 获得训练数据集
imgs, labels = train_set[0], train_set[1]
elif mode == 'valid':
# 获得验证数据集
imgs, labels = val_set[0], val_set[1]
elif mode == 'eval':
# 获得测试数据集
imgs, labels = eval_set[0], eval_set[1]
else:
raise Exception("mode can only be one of ['train', 'valid', 'eval']")
#校验数据
imgs_length = len(imgs)
assert len(imgs) == len(labels), \
"length of train_imgs({}) should be the same as train_labels({})".format(
len(imgs), len(labels))
# 定义数据集每个数据的序号, 根据序号读取数据
index_list = list(range(imgs_length))
# 读入数据时用到的batchsize
BATCHSIZE = 100
# 定义数据生成器
def data_generator():
if mode == 'train':
random.shuffle(index_list)
imgs_list = []
labels_list = []
for i in index_list:
img = np.array(imgs[i]).astype('float32')
label = np.array(labels[i]).astype('float32')
# 在使用卷积神经网络结构时,uncomment 下面两行代码
img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
label = np.reshape(labels[i], [1]).astype('float32')
imgs_list.append(img)
labels_list.append(label)
if len(imgs_list) == BATCHSIZE:
yield np.array(imgs_list), np.array(labels_list)
imgs_list = []
labels_list = []
# 如果剩余数据的数目小于BATCHSIZE,
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
yield np.array(imgs_list), np.array(labels_list)
return data_generator2 经典的全连接神经网络
经典的全连接神经网络来包含四层网络:输入层、两个隐含层和输出层,将手写数字识别任务通过全连接神经网络表示,如 图3 所示。
- 输入层:将数据输入给神经网络。在该任务中,输入层的尺度为28×28的像素值。
- 隐含层:增加网络深度和复杂度,隐含层的节点数是可以调整的,节点数越多,神经网络表示能力越强,参数量也会增加。在该任务中,中间的两个隐含层为10×10的结构,通常隐含层会比输入层的尺寸小,以便对关键信息做抽象,激活函数使用常见的Sigmoid函数。
- 输出层:输出网络计算结果,输出层的节点数是固定的。如果是回归问题,节点数量为需要回归的数字数量。如果是分类问题,则是分类标签的数量。在该任务中,模型的输出是回归一个数字,输出层的尺寸为1。
说明:
隐含层引入非线性激活函数Sigmoid是为了增加神经网络的非线性能力。
举例来说,如果一个神经网络采用线性变换,有四个输入x1x_1x1~x4x_4x4,一个输出yyy。假设第一层的变换是z1=x1−x2z_1=x_1-x_2z1=x1−x2和z2=x3+x4z_2=x_3+x_4z2=x3+x4,第二层的变换是y=z1+z2y=z_1+z_2y=z1+z2,则将两层的变换展开后得到y=x1−x2+x3+x4y=x_1-x_2+x_3+x_4y=x1−x2+x3+x4。也就是说,无论中间累积了多少层线性变换,原始输入和最终输出之间依然是线性关系。
Sigmoid 是早期神经网络模型中常见的非线性变换函数,通过如下代码,绘制出Sigmoid的函数曲线。
def sigmoid(x):
# 直接返回sigmoid函数
return 1. / (1. + np.exp(-x))
# param:起点,终点,间距
x = np.arange(-8, 8, 0.2)
y = sigmoid(x)
plt.plot(x, y)
plt.show()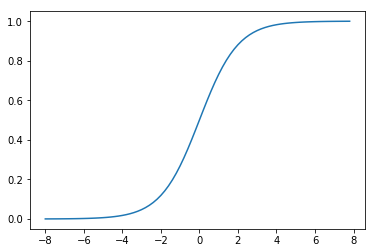
针对手写数字识别的任务,网络层的设计如下:
- 输入层的尺度为28×28,但批次计算的时候会统一加1个维度(大小为batch size)。
- 中间的两个隐含层为10×10的结构,激活函数使用常见的Sigmoid函数。
- 与房价预测模型一样,模型的输出是回归一个数字,输出层的尺寸设置成1。
下述代码为经典全连接神经网络的实现。完成网络结构定义后,即可训练神经网络。
import paddle.nn.functional as F
from paddle.nn import Linear
# 定义多层全连接神经网络
class MNIST(paddle.nn.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义两层全连接隐含层,输出维度是10,当前设定隐含节点数为10,可根据任务调整
self.fc1 = Linear(in_features=784, out_features=10)
self.fc2 = Linear(in_features=10, out_features=10)
# 定义一层全连接输出层,输出维度是1
self.fc3 = Linear(in_features=10, out_features=1)
# 定义网络的前向计算,隐含层激活函数为sigmoid,输出层不使用激活函数
def forward(self, inputs):
# inputs = paddle.reshape(inputs, [inputs.shape[0], 784])
outputs1 = self.fc1(inputs)
outputs1 = F.sigmoid(outputs1)
outputs2 = self.fc2(outputs1)
outputs2 = F.sigmoid(outputs2)
outputs_final = self.fc3(outputs2)
return outputs_final3 卷积神经网络
虽然使用经典的全连接神经网络可以提升一定的准确率,但其输入数据的形式导致丢失了图像像素间的空间信息,这影响了网络对图像内容的理解。对于计算机视觉问题,效果最好的模型仍然是卷积神经网络。卷积神经网络针对视觉问题的特点进行了网络结构优化,可以直接处理原始形式的图像数据,保留像素间的空间信息,因此更适合处理视觉问题。
卷积神经网络由多个卷积层和池化层组成,如 图4 所示。卷积层负责对输入进行扫描以生成更抽象的特征表示,池化层对这些特征表示进行过滤,保留最关键的特征信息。
两层卷积和池化的神经网络实现如下所示。
# 定义 SimpleNet 网络结构
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2
self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
# 定义池化层,池化核的大小kernel_size为2,池化步长为2
self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2
self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
# 定义池化层,池化核的大小kernel_size为2,池化步长为2
self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
# 定义一层全连接层,输出维度是1
self.fc = Linear(in_features=980, out_features=1)
# 定义网络前向计算过程,卷积后紧接着使用池化层,最后使用全连接层计算最终输出
# 卷积层激活函数使用Relu,全连接层不使用激活函数
def forward(self, inputs):
x = self.conv1(inputs)
x = F.relu(x)
x = self.max_pool1(x)
x = self.conv2(x)
x = F.relu(x)
x = self.max_pool2(x)
x = paddle.reshape(x, [x.shape[0], -1])
x = self.fc(x)
return x使用MNIST数据集训练定义好的卷积神经网络,如下所示。
说明:
以上数据加载函数load_data返回一个数据迭代器train_loader,该train_loader在每次迭代时的数据shape为[batch_size, 784],因此需要将该数据形式reshape为图像数据形式[batch_size, 1, 28, 28],其中第二维代表图像的通道数(在MNIST数据集中每张图片的通道数为1,传统RGB图片通道数为3)。
#网络结构部分之后的代码,保持不变
def train(model):
model.train()
#调用加载数据的函数,获得MNIST训练数据集
train_loader = load_data('train')
# 使用SGD优化器,learning_rate设置为0.01
opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# 训练5轮
EPOCH_NUM = 10
# MNIST图像高和宽
IMG_ROWS, IMG_COLS = 28, 28
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
images, labels = data
images = paddle.to_tensor(images)
labels = paddle.to_tensor(labels)
#前向计算的过程
predicts = model(images)
#计算损失,取一个批次样本损失的平均值
loss = F.square_error_cost(predicts, labels)
avg_loss = paddle.mean(loss)
#每训练200批次的数据,打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播,更新参数的过程
avg_loss.backward()
# 最小化loss,更新参数
opt.step()
# 清除梯度
opt.clear_grad()
#保存模型参数
paddle.save(model.state_dict(), 'mnist.pdparams')
model = MNIST()
train(model)比较经典全连接神经网络和卷积神经网络的损失变化,可以发现卷积神经网络的损失值下降更快,且最终的损失值更小。
二 损失函数
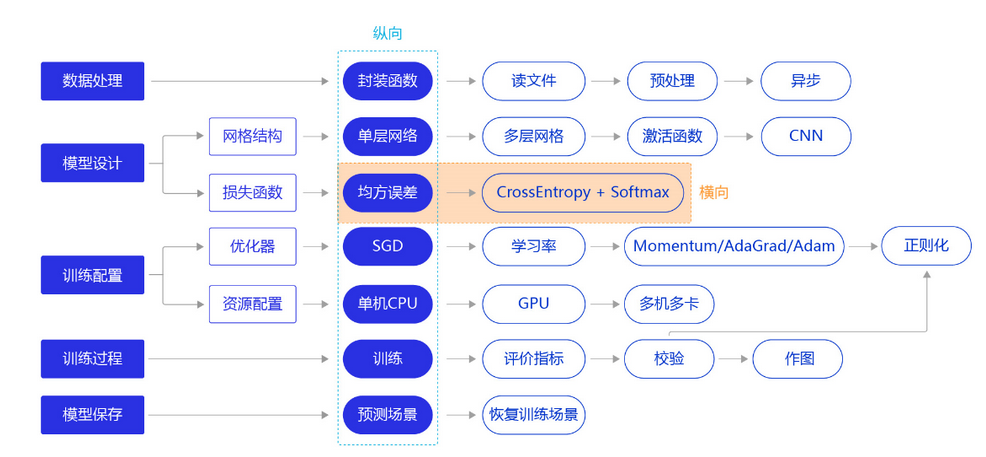
上一节我们尝试通过更复杂的模型(经典的全连接神经网络和卷积神经网络),提升手写数字识别模型训练的准确性。本节我们继续将“横纵式”教学法从横向展开,如 图1 所示,探讨损失函数的优化对模型训练效果的影响。
损失函数是模型优化的目标,用于在众多的参数取值中,识别最理想的取值。损失函数的计算在训练过程的代码中,每一轮模型训练的过程都相同,分如下三步:
- 先根据输入数据正向计算预测输出。
- 再根据预测值和真实值计算损失。
- 最后根据损失反向传播梯度并更新参数。
1 分类任务的损失函数
在之前的方案中,我们复用了房价预测模型的损失函数-均方误差。从预测效果来看,虽然损失不断下降,模型的预测值逐渐逼近真实值,但模型的最终效果不够理想。究其根本,不同的深度学习任务需要有各自适宜的损失函数。我们以房价预测和手写数字识别两个任务为例,详细剖析其中的缘由如下:
- 房价预测是回归任务,而手写数字识别是分类任务,使用均方误差作为分类任务的损失函数存在逻辑和效果上的缺欠。
- 房价可以是大于0的任何浮点数,而手写数字识别的输出只可能是0~9之间的10个整数,相当于一种标签。
- 在房价预测的案例中,由于房价本身是一个连续的实数值,因此以模型输出的数值和真实房价差距作为损失函数(Loss)是符合道理的。但对于分类问题,真实结果是分类标签,而模型输出是实数值,导致以两者相减作为损失不具备物理含义。
那么,什么是分类任务的合理输出呢?分类任务本质上是“某种特征组合下的分类概率”,下面以一个简单案例说明,如 图2 所示。
在本案例中,医生根据肿瘤大小xxx作为肿瘤性质yyy的参考判断(判断的因素有很多,肿瘤大小只是其中之一),那么我们观测到该模型判断的结果是xxx和yyy的标签(1为恶性,0为良性)。而这个数据背后的规律是不同大小的肿瘤,属于恶性肿瘤的概率。观测数据是真实规律抽样下的结果,分类模型应该拟合这个真实规律,输出属于该分类标签的概率。
2 Softmax函数
如果模型能输出10个标签的概率,对应真实标签的概率输出尽可能接近100%,而其他标签的概率输出尽可能接近0%,且所有输出概率之和为1。这是一种更合理的假设!与此对应,真实的标签值可以转变成一个10维度的one-hot向量,在对应数字的位置上为1,其余位置为0,比如标签“6”可以转变成[0,0,0,0,0,0,1,0,0,0]。
为了实现上述思路,需要引入Softmax函数,它可以将原始输出转变成对应标签的概率,公式如下,其中CCC是标签类别个数。
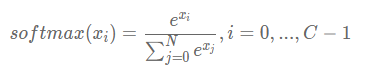
从公式的形式可见,每个输出的范围均在0~1之间,且所有输出之和等于1,这是这种变换后可被解释成概率的基本前提。对应到代码上,需要在前向计算中,对全连接网络的输出层增加一个Softmax运算,outputs = F.softmax(outputs)。
图3 是一个三个标签的分类模型(三分类)使用的Softmax输出层,从中可见原始输出的三个数字3、1、-3,经过Softmax层后转变成加和为1的三个概率值0.88、0.12、0。
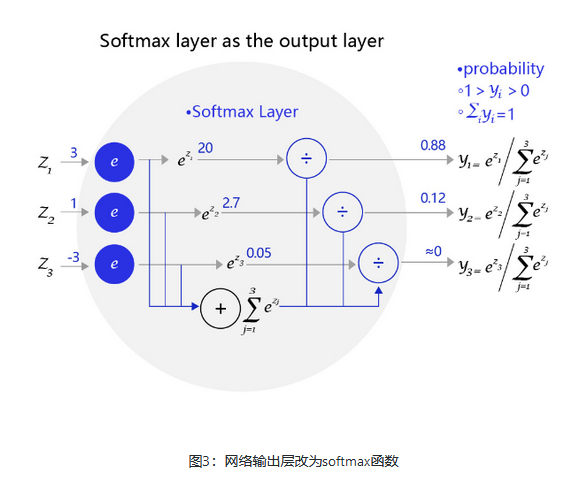
上文解释了为何让分类模型的输出拟合概率的原因,但为何偏偏用Softmax函数完成这个职能? 下面以二分类问题(只输出两个标签)进行原理的探讨。
对于二分类问题,使用两个输出接入Softmax作为输出层,等价于使用单一输出接入Sigmoid函数。如 图4 所示,利用两个标签的输出概率之和为1的条件,Softmax输出0.6和0.4两个标签概率,从数学上等价于输出一个标签的概率0.6。
3 交叉熵
在模型输出为分类标签的概率时,直接以标签和概率做比较也不够合理,人们更习惯使用交叉熵误差作为分类问题的损失衡量。
交叉熵损失函数的设计是基于最大似然思想:最大概率得到观察结果的假设是真的。如何理解呢?举个例子来说,如 图7 所示。有两个外形相同的盒子,甲盒中有99个白球,1个蓝球;乙盒中有99个蓝球,1个白球。一次试验取出了一个蓝球,请问这个球应该是从哪个盒子中取出的?
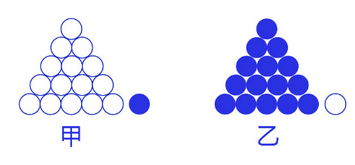
相信大家简单思考后均会得出更可能是从乙盒中取出的,因为从乙盒中取出一个蓝球的概率更高(P(D∣h))(P(D|h))(P(D∣h)),所以观察到一个蓝球更可能是从乙盒中取出的(P(h∣D))(P(h|D))(P(h∣D))。DDD是观测的数据,即蓝球白球;hhh是模型,即甲盒乙盒。这就是贝叶斯公式所表达的思想:
![]()
依据贝叶斯公式,某二分类模型“生成”nnn个训练样本的概率:
![]()
经过公式推导,使得上述概率最大等价于最小化交叉熵,得到交叉熵的损失函数。交叉熵的公式如下:
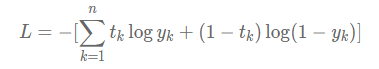
其中,log表示以e为底数的自然对数。y_k代表模型输出,t_k代表各个标签。t_k中只有正确解的标签为1,其余均为0(one-hot表示)。
因此,交叉熵只计算对应着“正确解”标签的输出的自然对数。比如,假设正确标签的索引是“2”,与之对应的神经网络的输出是0.6,则交叉熵误差是−log0.6=0.51−\log 0.6 = 0.51−log0.6=0.51;若“2”对应的输出是0.1,则交叉熵误差为−log0.1=2.30−\log 0.1 = 2.30−log0.1=2.30。由此可见,交叉熵误差的值是由正确标签所对应的输出结果决定的。
自然对数的函数曲线可由如下代码实现。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0.01,1,0.01)
y = np.log(x)
plt.title("y=log(x)")
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x,y)
plt.show()
plt.figure()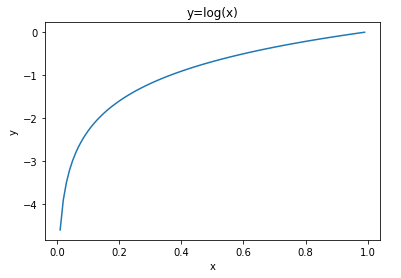
如自然对数的图形所示,当x等于1时,y为0;随着x向0靠近,y逐渐变小。因此,正确解标签对应的输出越大,交叉熵的值越接近0;当输出为1时,交叉熵误差为0。反之,如果正确解标签对应的输出越小,则交叉熵的值越大。
4 交叉熵的代码实现
在手写数字识别任务中,仅改动三行代码,就可以将在现有模型的损失函数替换成交叉熵(Cross_entropy)。
- 在读取数据部分,将标签的类型设置成int,体现它是一个标签而不是实数值(飞桨框架默认将标签处理成int64)。
- 在网络定义部分,将输出层改成“输出十个标签的概率”的模式。
- 在训练过程部分,将损失函数从均方误差换成交叉熵。
在数据处理部分,需要修改标签变量Label的格式,代码如下所示。
- 从:label = np.reshape(labels[i], [1]).astype(‘float32’)
- 到:label = np.reshape(labels[i], [1]).astype(‘int64’)
在网络定义部分,需要修改输出层结构,代码如下所示。
- 从:self.fc = Linear(in_features=980, out_features=1)
- 到:self.fc = Linear(in_features=980, out_features=10)
#数据处理部分之前的代码,保持不变
import os
import random
import paddle
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
import gzip
import json
# 创建一个类MnistDataset,继承paddle.io.Dataset 这个类
# MnistDataset的作用和上面load_data()函数的作用相同,均是构建一个迭代器
class MnistDataset(paddle.io.Dataset):
def __init__(self, mode):
datafile = './work/mnist.json.gz'
data = json.load(gzip.open(datafile))
# 读取到的数据区分训练集,验证集,测试集
train_set, val_set, eval_set = data
# 数据集相关参数,图片高度IMG_ROWS, 图片宽度IMG_COLS
self.IMG_ROWS = 28
self.IMG_COLS = 28
if mode=='train':
# 获得训练数据集
imgs, labels = train_set[0], train_set[1]
elif mode=='valid':
# 获得验证数据集
imgs, labels = val_set[0], val_set[1]
elif mode=='eval':
# 获得测试数据集
imgs, labels = eval_set[0], eval_set[1]
else:
raise Exception("mode can only be one of ['train', 'valid', 'eval']")
# 校验数据
imgs_length = len(imgs)
assert len(imgs) == len(labels), \
"length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(labels))
self.imgs = imgs
self.labels = labels
def __getitem__(self, idx):
# img = np.array(self.imgs[idx]).astype('float32')
# label = np.array(self.labels[idx]).astype('int64')
img = np.reshape(self.imgs[idx], [1, self.IMG_ROWS, self.IMG_COLS]).astype('float32')
label = np.reshape(self.labels[idx], [1]).astype('int64')
return img, label
def __len__(self):
return len(self.imgs)
# 声明数据加载函数,使用训练模式,MnistDataset构建的迭代器每次迭代只返回batch=1的数据
train_dataset = MnistDataset(mode='train')
# 使用paddle.io.DataLoader 定义DataLoader对象用于加载Python生成器产生的数据,
# DataLoader 返回的是一个批次数据迭代器,并且是异步的;
train_loader = paddle.io.DataLoader(train_dataset, batch_size=100, shuffle=True, drop_last=True)
val_dataset = MnistDataset(mode='valid')
val_loader = paddle.io.DataLoader(val_dataset, batch_size=128,drop_last=True)在网络定义部分,需要修改输出层结构,代码如下所示。
- 从:self.fc = Linear(in_features=980, out_features=1)
- 到:self.fc = Linear(in_features=980, out_features=10)
# 定义 SimpleNet 网络结构
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2
self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
# 定义池化层,池化核的大小kernel_size为2,池化步长为2
self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2
self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
# 定义池化层,池化核的大小kernel_size为2,池化步长为2
self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
# 定义一层全连接层,输出维度是10
self.fc = Linear(in_features=980, out_features=10)
# 定义网络前向计算过程,卷积后紧接着使用池化层,最后使用全连接层计算最终输出
# 卷积层激活函数使用Relu,全连接层激活函数使用softmax
def forward(self, inputs):
x = self.conv1(inputs)
x = F.relu(x)
x = self.max_pool1(x)
x = self.conv2(x)
x = F.relu(x)
x = self.max_pool2(x)
x = paddle.reshape(x, [x.shape[0], 980])
x = self.fc(x)
return x修改计算损失的函数,从均方误差(常用于回归问题)到交叉熵误差(常用于分类问题),代码如下所示。
- 从:loss = paddle.nn.functional.square_error_cost(predict, label)
- 到:loss = paddle.nn.functional.cross_entropy(predict, label)
def evaluation(model, datasets):
model.eval()
acc_set = list()
for batch_id, data in enumerate(datasets()):
images, labels = data
images = paddle.to_tensor(images)
labels = paddle.to_tensor(labels)
pred = model(images) # 获取预测值
acc = paddle.metric.accuracy(input=pred, label=labels)
acc_set.extend(acc.numpy())
# #计算多个batch的准确率
acc_val_mean = np.array(acc_set).mean()
return acc_val_mean#仅修改计算损失的函数,从均方误差(常用于回归问题)到交叉熵误差(常用于分类问题)
def train(model):
model.train()
#调用加载数据的函数
# train_loader = load_data('train')
# val_loader = load_data('valid')
opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
EPOCH_NUM = 10
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
images, labels = data
images = paddle.to_tensor(images)
labels = paddle.to_tensor(labels)
#前向计算的过程
predicts = model(images)
#计算损失,使用交叉熵损失函数,取一个批次样本损失的平均值
loss = F.cross_entropy(predicts, labels)
avg_loss = paddle.mean(loss)
#每训练了200批次的数据,打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播,更新参数的过程
avg_loss.backward()
# 最小化loss,更新参数
opt.step()
# 清除梯度
opt.clear_grad()
# acc_train_mean = evaluation(model, train_loader)
# acc_val_mean = evaluation(model, val_loader)
# print('train_acc: {}, val acc: {}'.format(acc_train_mean, acc_val_mean))
#保存模型参数
paddle.save(model.state_dict(), 'mnist.pdparams')
#创建模型
model = MNIST()
#启动训练过程
train(model)虽然上述训练过程的损失明显比使用均方误差算法要小,但因为损失函数量纲的变化,我们无法从比较两个不同的Loss得出谁更加优秀。怎么解决这个问题呢?我们可以回归到问题的本质,谁的分类准确率更高来判断。在后面介绍完计算准确率和作图的内容后,读者可以自行测试采用不同损失函数下,模型准确率的高低。
至此,大家阅读论文中常见的一些分类任务模型图就清晰明了,如全连接神经网络、卷积神经网络,在模型的最后阶段,都是使用Softmax进行处理。
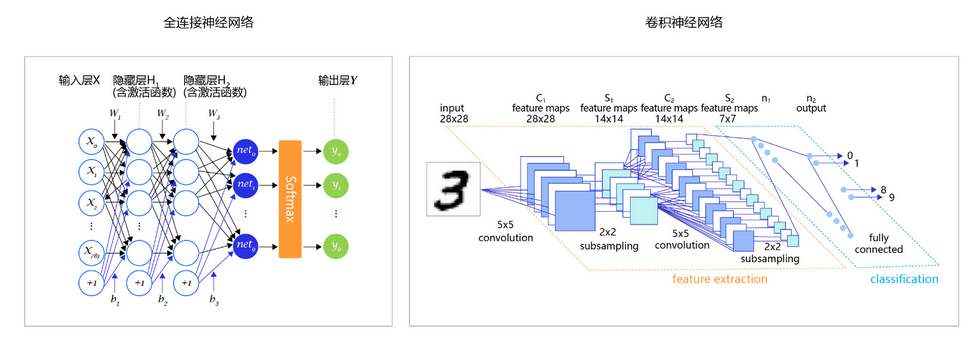
由于我们修改了模型的输出格式,因此使用模型做预测时的代码也需要做相应的调整。从模型输出10个标签的概率中选择最大的,将其标签编号输出。
# 读取一张本地的样例图片,转变成模型输入的格式
def load_image(img_path):
# 从img_path中读取图像,并转为灰度图
im = Image.open(img_path).convert('L')
im = im.resize((28, 28), Image.ANTIALIAS)
im = np.array(im).reshape(1, 1, 28, 28).astype(np.float32)
# 图像归一化
im = 1.0 - im / 255.
return im
# 定义预测过程
model = MNIST()
params_file_path = 'mnist.pdparams'
img_path = 'work/example_0.jpg'
# 加载模型参数
param_dict = paddle.load(params_file_path)
model.load_dict(param_dict)
# 灌入数据
model.eval()
tensor_img = load_image(img_path)
#模型反馈10个分类标签的对应概率
results = model(paddle.to_tensor(tensor_img))
#取概率最大的标签作为预测输出
lab = np.argsort(results.numpy())
print("本次预测的数字是: ", lab[0][-1])三 优化算法
上一节我们明确了分类任务的损失函数(优化目标)的相关概念和实现方法,本节我们依旧横向展开"横纵式"教学法,如 图1 所示,本节主要探讨在手写数字识别任务中,使得损失达到最小的参数取值的实现方法。
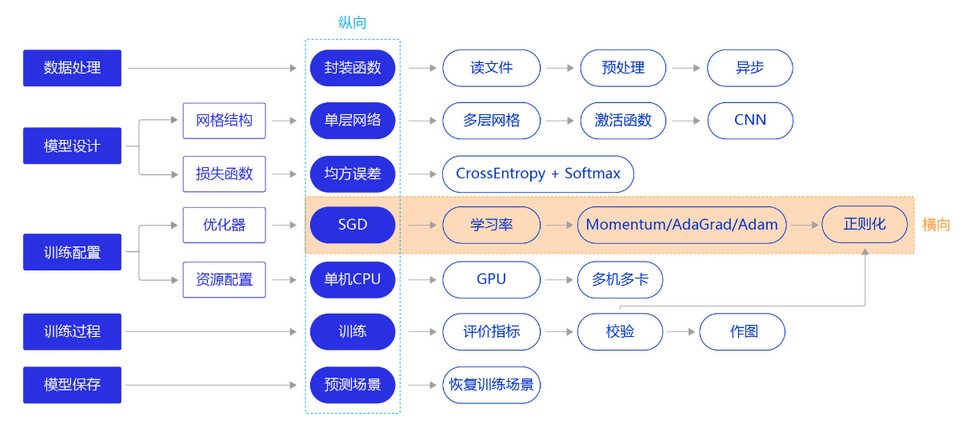
前提条件
在优化算法之前,需要进行数据处理、设计神经网络结构,代码与上一节保持一致。
# 加载相关库
import os
import random
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import numpy as np
from PIL import Image
import gzip
import json
# 定义数据集读取器
def load_data(mode='train'):
# 读取数据文件
datafile = './work/mnist.json.gz'
print('loading mnist dataset from {} ......'.format(datafile))
data = json.load(gzip.open(datafile))
# 读取数据集中的训练集,验证集和测试集
train_set, val_set, eval_set = data
# 数据集相关参数,图片高度IMG_ROWS, 图片宽度IMG_COLS
IMG_ROWS = 28
IMG_COLS = 28
# 根据输入mode参数决定使用训练集,验证集还是测试
if mode == 'train':
imgs = train_set[0]
labels = train_set[1]
elif mode == 'valid':
imgs = val_set[0]
labels = val_set[1]
elif mode == 'eval':
imgs = eval_set[0]
labels = eval_set[1]
# 获得所有图像的数量
imgs_length = len(imgs)
# 验证图像数量和标签数量是否一致
assert len(imgs) == len(labels), \
"length of train_imgs({}) should be the same as train_labels({})".format(
len(imgs), len(labels))
index_list = list(range(imgs_length))
# 读入数据时用到的batchsize
BATCHSIZE = 100
# 定义数据生成器
def data_generator():
# 训练模式下,打乱训练数据
if mode == 'train':
random.shuffle(index_list)
imgs_list = []
labels_list = []
# 按照索引读取数据
for i in index_list:
# 读取图像和标签,转换其尺寸和类型
img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
label = np.reshape(labels[i], [1]).astype('int64')
imgs_list.append(img)
labels_list.append(label)
# 如果当前数据缓存达到了batch size,就返回一个批次数据
if len(imgs_list) == BATCHSIZE:
yield np.array(imgs_list), np.array(labels_list)
# 清空数据缓存列表
imgs_list = []
labels_list = []
# 如果剩余数据的数目小于BATCHSIZE,
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
yield np.array(imgs_list), np.array(labels_list)
return data_generator
# 定义模型结构
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2
self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
# 定义池化层,池化核的大小kernel_size为2,池化步长为2
self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2
self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
# 定义池化层,池化核的大小kernel_size为2,池化步长为2
self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
# 定义一层全连接层,输出维度是10
self.fc = Linear(in_features=980, out_features=10)
# 定义网络前向计算过程,卷积后紧接着使用池化层,最后使用全连接层计算最终输出
# 卷积层激活函数使用Relu,全连接层激活函数使用softmax
def forward(self, inputs):
x = self.conv1(inputs)
x = F.relu(x)
x = self.max_pool1(x)
x = self.conv2(x)
x = F.relu(x)
x = self.max_pool2(x)
x = paddle.reshape(x, [x.shape[0], -1])
x = self.fc(x)
return x1 设置学习率
在深度学习神经网络模型中,通常使用标准的随机梯度下降算法更新参数,学习率代表参数更新幅度的大小,即步长。当学习率最优时,模型的有效容量最大,最终能达到的效果最好。学习率和深度学习任务类型有关,合适的学习率往往需要大量的实验和调参经验。探索学习率最优值时需要注意如下两点:
- 学习率不是越小越好。学习率越小,损失函数的变化速度越慢,意味着我们需要花费更长的时间进行收敛,如 图2 左图所示。
- 学习率不是越大越好。只根据总样本集中的一个批次计算梯度,抽样误差会导致计算出的梯度不是全局最优的方向,且存在波动。在接近最优解时,过大的学习率会导致参数在最优解附近震荡,损失难以收敛。
在训练前,我们往往不清楚一个特定问题设置成怎样的学习率是合理的,因此在训练时可以尝试调小或调大,通过观察Loss下降的情况判断合理的学习率,设置学习率的代码如下所示。
#仅优化算法的设置有所差别
def train(model):
model.train()
#调用加载数据的函数
train_loader = load_data('train')
#设置不同初始学习率
opt = paddle.optimizer.SGD(learning_rate=0.001, parameters=model.parameters())
# opt = paddle.optimizer.SGD(learning_rate=0.0001, parameters=model.parameters())
# opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
EPOCH_NUM = 10
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
images, labels = data
images = paddle.to_tensor(images)
labels = paddle.to_tensor(labels)
#前向计算的过程
predicts = model(images)
#计算损失,取一个批次样本损失的平均值
loss = F.cross_entropy(predicts, labels)
avg_loss = paddle.mean(loss)
#每训练了100批次的数据,打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播,更新参数的过程
avg_loss.backward()
# 最小化loss,更新参数
opt.step()
# 清除梯度
opt.clear_grad()
#保存模型参数
paddle.save(model.state_dict(), 'mnist.pdparams')
#创建模型
model = MNIST()
#启动训练过程
train(model)2 学习率的主流优化算法
学习率是优化器的一个参数,调整学习率看似是一件非常麻烦的事情,需要不断的调整步长,观察训练时间和Loss的变化。经过研究员的不断的实验,当前已经形成了四种比较成熟的优化算法:SGD、Momentum、AdaGrad和Adam,效果如 图3 所示。
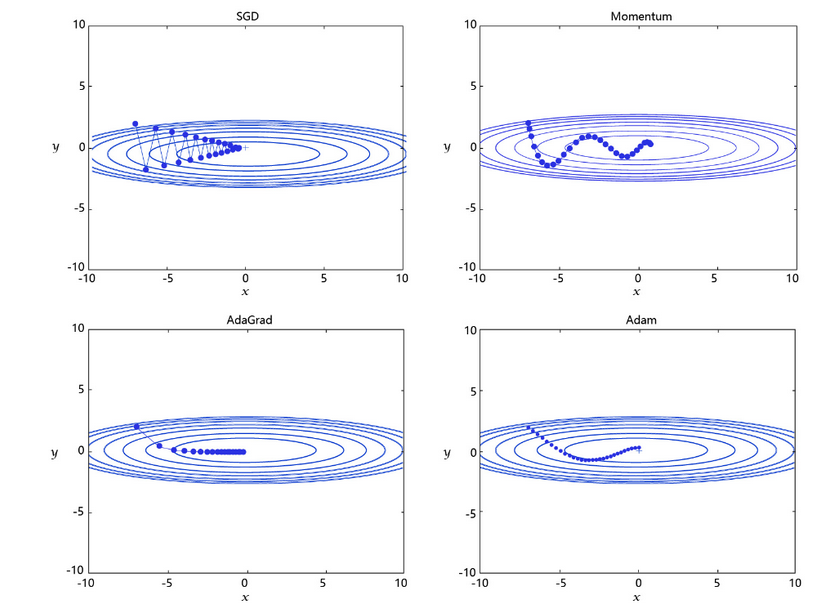
-
SGD: 随机梯度下降算法,每次训练少量数据,抽样偏差导致的参数收敛过程中震荡。
-
Momentum: 引入物理“动量”的概念,累积速度,减少震荡,使参数更新的方向更稳定。
每个批次的数据含有抽样误差,导致梯度更新的方向波动较大。如果我们引入物理动量的概念,给梯度下降的过程加入一定的“惯性”累积,就可以减少更新路径上的震荡,即每次更新的梯度由“历史多次梯度的累积方向”和“当次梯度”加权相加得到。历史多次梯度的累积方向往往是从全局视角更正确的方向,这与“惯性”的物理概念很像,也是为何其起名为“Momentum”的原因。类似不同品牌和材质的篮球有一定的重量差别,街头篮球队中的投手(擅长中远距离投篮)喜欢稍重篮球的比例较高。一个很重要的原因是,重的篮球惯性大,更不容易受到手势的小幅变形或风吹的影响。
- AdaGrad: 根据不同参数距离最优解的远近,动态调整学习率。学习率逐渐下降,依据各参数变化大小调整学习率。
通过调整学习率的实验可以发现:当某个参数的现值距离最优解较远时(表现为梯度的绝对值较大),我们期望参数更新的步长大一些,以便更快收敛到最优解。当某个参数的现值距离最优解较近时(表现为梯度的绝对值较小),我们期望参数的更新步长小一些,以便更精细的逼近最优解。类似于打高尔夫球,专业运动员第一杆开球时,通常会大力打一个远球,让球尽量落在洞口附近。当第二杆面对离洞口较近的球时,他会更轻柔而细致的推杆,避免将球打飞。与此类似,参数更新的步长应该随着优化过程逐渐减少,减少的程度与当前梯度的大小有关。根据这个思想编写的优化算法称为“AdaGrad”,Ada是Adaptive的缩写,表示“适应环境而变化”的意思。RMSProp是在AdaGrad基础上的改进,学习率随着梯度变化而适应,解决AdaGrad学习率急剧下降的问题。
- Adam: 由于动量和自适应学习率两个优化思路是正交的,因此可以将两个思路结合起来,这就是当前广泛应用的算法。
我们可以尝试选择不同的优化算法训练模型,观察训练时间和损失变化的情况,代码实现如下。
#仅优化算法的设置有所差别
def train(model):
model.train()
#调用加载数据的函数
train_loader = load_data('train')
#四种优化算法的设置方案,可以逐一尝试效果
opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# opt = paddle.optimizer.Momentum(learning_rate=0.01, momentum=0.9, parameters=model.parameters())
# opt = paddle.optimizer.Adagrad(learning_rate=0.01, parameters=model.parameters())
# opt = paddle.optimizer.Adam(learning_rate=0.01, parameters=model.parameters())
EPOCH_NUM = 3
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
images, labels = data
images = paddle.to_tensor(images)
labels = paddle.to_tensor(labels)
#前向计算的过程
predicts = model(images)
#计算损失,取一个批次样本损失的平均值
loss = F.cross_entropy(predicts, labels)
avg_loss = paddle.mean(loss)
#每训练了100批次的数据,打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播,更新参数的过程
avg_loss.backward()
# 最小化loss,更新参数
opt.step()
# 清除梯度
opt.clear_grad()
#保存模型参数
paddle.save(model.state_dict(), 'mnist.pdparams')
#创建模型
model = MNIST()
#启动训练过程
train(model)