要点：

资源配置
训练调试
恢复训练
模型部署

参考文档： paddle官方文档

一资源配置

1 概述

从前几节的训练看，无论是房价预测任务还是MNIST手写字数字识别任务，训练好一个模型不会超过10分钟，主要原因是我们所使用的神经网络比较简单。但实际应用时，常会遇到更加复杂的机器学习或深度学习任务，需要运算速度更高的硬件（如GPU、NPU），甚至同时使用多个机器共同训练一个任务（多卡训练和多机训练）。本节我们依旧横向展开"横纵式"教学方法，如图1 所示，探讨在手写数字识别任务中，通过资源配置的优化，提升模型训练效率的方法。

前提条件

需要先进行数据处理、设计神经网络结构，代码与上一节保持一致，如下所示。

# 加载相关库
import os
import random
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import numpy as np
from PIL import Image
import gzip
import json

# 定义数据集读取器
def load_data(mode='train'):

    # 读取数据文件
    datafile = './work/mnist.json.gz'
    print('loading mnist dataset from {} ......'.format(datafile))
    data = json.load(gzip.open(datafile))
    # 读取数据集中的训练集，验证集和测试集
    train_set, val_set, eval_set = data

    # 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
    IMG_ROWS = 28
    IMG_COLS = 28
    # 根据输入mode参数决定使用训练集，验证集还是测试
    if mode == 'train':
        imgs = train_set[0]
        labels = train_set[1]
    elif mode == 'valid':
        imgs = val_set[0]
        labels = val_set[1]
    elif mode == 'eval':
        imgs = eval_set[0]
        labels = eval_set[1]
    # 获得所有图像的数量
    imgs_length = len(imgs)
    # 验证图像数量和标签数量是否一致
    assert len(imgs) == len(labels), \
          "length of train_imgs({}) should be the same as train_labels({})".format(
                  len(imgs), len(labels))

    index_list = list(range(imgs_length))

    # 读入数据时用到的batchsize
    BATCHSIZE = 100

    # 定义数据生成器
    def data_generator():
        # 训练模式下，打乱训练数据
        if mode == 'train':
            random.shuffle(index_list)
        imgs_list = []
        labels_list = []
        # 按照索引读取数据
        for i in index_list:
            # 读取图像和标签，转换其尺寸和类型
            img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
            label = np.reshape(labels[i], [1]).astype('int64')
            imgs_list.append(img) 
            labels_list.append(label)
            # 如果当前数据缓存达到了batch size，就返回一个批次数据
            if len(imgs_list) == BATCHSIZE:
                yield np.array(imgs_list), np.array(labels_list)
                # 清空数据缓存列表
                imgs_list = []
                labels_list = []

        # 如果剩余数据的数目小于BATCHSIZE，
        # 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
        if len(imgs_list) > 0:
            yield np.array(imgs_list), np.array(labels_list)

    return data_generator

# 定义模型结构
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):
     def __init__(self):
         super(MNIST, self).__init__()
         
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化核的大小kernel_size为2，池化步长为2
         self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化核的大小kernel_size为2，池化步长为2
         self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
         # 定义一层全连接层，输出维度是10
         self.fc = Linear(in_features=980, out_features=10)
         
   # 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出
   # 卷积层激活函数使用Relu，全连接层激活函数使用softmax
     def forward(self, inputs):
         x = self.conv1(inputs)
         x = F.relu(x)
         x = self.max_pool1(x)
         x = self.conv2(x)
         x = F.relu(x)
         x = self.max_pool2(x)
         x = paddle.reshape(x, [x.shape[0], 980])
         x = self.fc(x)
         return x

2 单GPU训练

通过paddle.set_device API，设置在GPU上训练还是CPU上训练。

paddle.set_device (device)

参数 device (str)：此参数确定特定的运行设备，可以是cpu、 gpu:x或者是xpu:x。其中，x是GPU或XPU的编号。当device是cpu时，程序在CPU上运行；当device是gpu:x时，程序在GPU上运行。

#仅优化算法的设置有所差别
def train(model):
    #开启GPU
    use_gpu = True
    paddle.set_device('gpu:0') if use_gpu else paddle.set_device('cpu')
    model.train()
    #调用加载数据的函数
    train_loader = load_data('train')
    
    #设置不同初始学习率
    opt = paddle.optimizer.Adam(learning_rate=0.01, parameters=model.parameters())
    
    EPOCH_NUM = 5
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，变得更加简洁
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            
            #前向计算的过程
            predicts = model(images)
            
            #计算损失，取一个批次样本损失的平均值
            loss = F.cross_entropy(predicts, labels)
            avg_loss = paddle.mean(loss)
            
            #每训练了100批次的数据，打印下当前Loss的情况
            if batch_id % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            opt.step()
            opt.clear_grad()

    #保存模型参数
    paddle.save(model.state_dict(), 'mnist.pdparams')
#创建模型    
model = MNIST()
#启动训练过程
train(model)

2 分布式训练

在工业实践中，很多较复杂的任务需要使用更强大的模型。强大模型加上海量的训练数据，经常导致模型训练耗时严重。比如在计算机视觉分类任务中，训练一个在ImageNet数据集上精度表现良好的模型，大概需要一周的时间，因为过程中我们需要不断尝试各种优化的思路和方案。如果每次训练均要耗时1周，这会大大降低模型迭代的速度。在机器资源充沛的情况下，建议采用分布式训练，大部分模型的训练时间可压缩到小时级别。

分布式训练有两种实现模式：模型并行和数据并行。

1 模型并行

模型并行是将一个网络模型拆分为多份，拆分后的模型分到多个设备上（GPU）训练，每个设备的训练数据是相同的。模型并行的实现模式可以节省内存，但是应用较为受限。

模型并行的方式一般适用于如下两个场景：

模型架构过大： 完整的模型无法放入单个GPU。如2012年ImageNet大赛的冠军模型AlexNet是模型并行的典型案例，由于当时GPU内存较小，单个GPU不足以承担AlexNet，因此研究者将AlexNet拆分为两部分放到两个GPU上并行训练。
网络模型的结构设计相对独立： 当网络模型的设计结构可以并行化时，采用模型并行的方式。如在计算机视觉目标检测任务中，一些模型（如YOLO9000）的边界框回归和类别预测是独立的，可以将独立的部分放到不同的设备节点上完成分布式训练。

2 数据并行

数据并行与模型并行不同，数据并行每次读取多份数据，读取到的数据输入给多个设备（GPU）上的模型，每个设备上的模型是完全相同的，飞桨采用的就是这种方式。

说明：

当前GPU硬件技术快速发展，深度学习使用的主流GPU的内存已经足以满足大多数的网络模型需求，所以大多数情况下使用数据并行的方式。

数据并行的方式与众人拾柴火焰高的道理类似，如果把训练数据比喻为砖头，把一个设备（GPU）比喻为一个人，那单GPU训练就是一个人在搬砖，多GPU训练就是多个人同时搬砖，每次搬砖的数量倍数增加，效率呈倍数提升。值得注意的是，每个设备的模型是完全相同的，但是输入数据不同，因此每个设备的模型计算出的梯度是不同的。如果每个设备的梯度只更新当前设备的模型，就会导致下次训练时，每个模型的参数都不相同。因此我们还需要一个梯度同步机制，保证每个设备的梯度是完全相同的。

梯度同步有两种方式：PRC通信方式和NCCL2通信方式（Nvidia Collective multi-GPU Communication Library）。

1 PRC通信方式

PRC通信方式通常用于CPU分布式训练，它有两个节点：参数服务器Parameter server和训练节点Trainer，结构如图2 所示

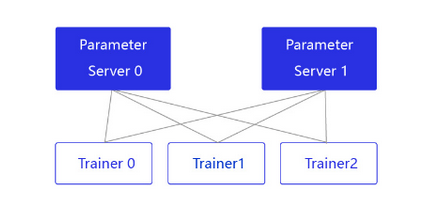
parameter server收集来自每个设备的梯度更新信息，并计算出一个全局的梯度更新。Trainer用于训练，每个Trainer上的程序相同，但数据不同。当Parameter server收到来自Trainer的梯度更新请求时，统一更新模型的梯度。

2 NCCL2通信方式（Collective）

当前飞桨的GPU分布式训练使用的是基于NCCL2的通信方式，结构如图3 所示。

相比PRC通信方式，使用NCCL2（Collective通信方式）进行分布式训练，不需要启动Parameter server进程，每个Trainer进程保存一份完整的模型参数，在完成梯度计算之后通过Trainer之间的相互通信，Reduce梯度数据到所有节点的所有设备，然后每个节点在各自完成参数更新。

飞桨提供了便利的数据并行训练方式，用户只需要对程序进行简单修改，即可实现在多GPU上并行训练。接下来将讲述如何将一个单机程序通过简单的改造，变成单机多卡程序。

单机多卡程序通过如下两步改动即可完成：

初始化并行环境。
使用paddle.DataParallel封装模型。

import paddle 
import paddle.distributed as dist

def train_multi_gpu(model):
    # 修改1- 初始化并行环境
    dist.init_parallel_env()
    # 修改2- 增加paddle.DataParallel封装
    model = paddle.DataParallel(model)
    model.train()
    #调用加载数据的函数
    train_loader = load_data('train')
    opt = paddle.optimizer.Adam(learning_rate=0.01, parameters=model.parameters())
    EPOCH_NUM = 5
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，变得更加简洁
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            #前向计算的过程
            predicts = model(images)
            #计算损失，取一个批次样本损失的平均值
            loss = F.cross_entropy(predicts, labels)
            avg_loss = paddle.mean(loss)
            #每训练了100批次的数据，打印下当前Loss的情况
            if batch_id % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
            #后向传播，更新参数的过程
            avg_loss.backward()
            opt.step()
            opt.clear_grad()

    #保存模型参数
    paddle.save(model.state_dict(), 'mnist.pdparams')

#创建模型    
model = MNIST()
#启动训练过程
train_multi_gpu(model)

启动多GPU的训练，有两种方式：

基于launch启动；
基于spawn方式启动。

说明：

AI Studio当前仅支持单卡GPU，因此本案例需要在本地GPU上执行，无法在AI Studio上演示。

1. 基于launch方式启动

需要在命令行中设置参数变量。打开终端，运行如下命令：

单机单卡启动，默认使用第0号卡。

$ python train.py

单机多卡启动，默认使用当前可见的所有卡。

$ python -m paddle.distributed.launch train.py

单机多卡启动，设置当前使用的第0号和第1号卡。

$ python -m paddle.distributed.launch --gpus '0,1' --log_dir ./mylog train.py

$ export CUDA_VISIABLE_DEVICES='0,1'
$ python -m paddle.distributed.launch train.py

2. 基于spawn方式启动

launch方式启动训练，是以文件为单位启动多进程，需要用户在启动时调用paddle.distributed.launch，对于进程的管理要求较高；飞桨最新版本中，增加了spawn启动方式，可以更好地控制进程，在日志打印、训练和退出时更加友好。spawn方式和launch方式仅在启动上有所区别。

# 启动train多进程训练，默认使用所有可见的GPU卡。
if __name__ == '__main__':
    dist.spawn(train)

# 启动train函数2个进程训练，默认使用当前可见的前2张卡。
if __name__ == '__main__':
    dist.spawn(train, nprocs=2)

# 启动train函数2个进程训练，默认使用第4号和第5号卡。
if __name__ == '__main__':
    dist.spawn(train, nprocs=2, selelcted_gpus='4,5')

二训练调试和优化

上一节我们研究了资源部署优化的方法，通过使用单GPU和分布式部署，提升模型训练的效率。本节我们依旧横向展开"横纵式"，如图1 所示，探讨在手写数字识别任务中，为了保证模型的真实效果，在模型训练部分，对模型进行一些调试和优化的方法。

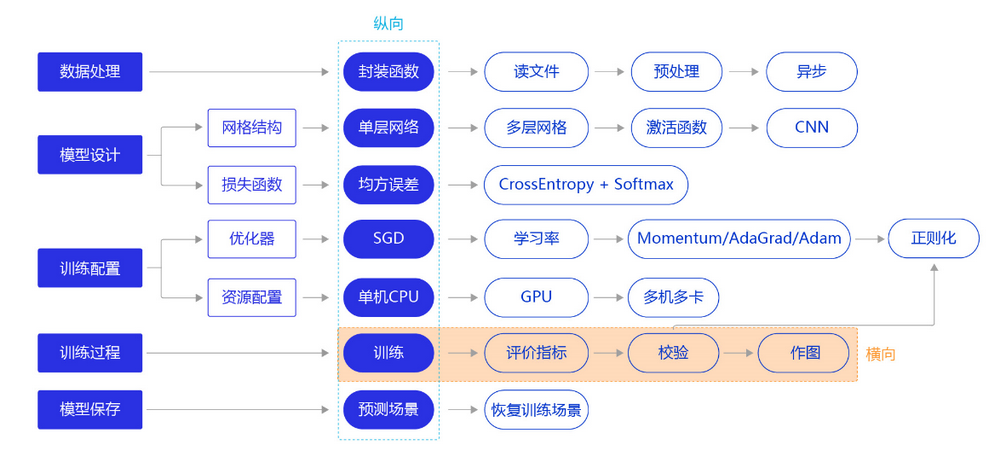
训练过程优化思路主要有如下五个关键环节：

1. 计算分类准确率，观测模型训练效果。

交叉熵损失函数只能作为优化目标，无法直接准确衡量模型的训练效果。准确率可以直接衡量训练效果，但由于其离散性质，不适合做为损失函数优化神经网络。

2. 检查模型训练过程，识别潜在问题。

如果模型的损失或者评估指标表现异常，通常需要打印模型每一层的输入和输出来定位问题，分析每一层的内容来获取错误的原因。

3. 加入校验或测试，更好评价模型效果。

理想的模型训练结果是在训练集和验证集上均有较高的准确率，如果训练集的准确率低于验证集，说明网络训练程度不够；如果训练集的准确率高于验证集，可能是发生了过拟合现象。通过在优化目标中加入正则化项的办法，解决过拟合的问题。

4. 加入正则化项，避免模型过拟合。

飞桨框架支持为整体参数加入正则化项，这是通常的做法。此外，飞桨框架也支持为某一层或某一部分的网络单独加入正则化项，以达到精细调整参数训练的效果。

5. 可视化分析。

用户不仅可以通过打印或使用matplotlib库作图，飞桨还提供了更专业的可视化分析工具VisualDL，提供便捷的可视化分析方法。

1 计算模型的分类准确率

准确率是一个直观衡量分类模型效果的指标，由于这个指标是离散的，因此不适合作为损失来优化。通常情况下，交叉熵损失越小的模型，分类的准确率也越高。基于分类准确率，我们可以公平地比较两种损失函数的优劣，例如在【手写数字识别】之损失函数章节中均方误差和交叉熵的比较。

使用飞桨提供的计算分类准确率API，可以直接计算准确率。

class paddle.metric.Accuracy

该API的输入参数input为预测的分类结果predict，输入参数label为数据真实的label。飞桨还提供了更多衡量模型效果的计算指标，详细可以查看paddle.meric包下面的API。

在下述代码中，我们在模型前向计算过程forward函数中计算分类准确率，并在训练时打印每个批次样本的分类准确率。

# 加载相关库
import os
import random
import paddle
import numpy as np
from PIL import Image
import gzip
import json


# 定义数据集读取器
def load_data(mode='train'):

    # 读取数据文件
    datafile = './work/mnist.json.gz'
    print('loading mnist dataset from {} ......'.format(datafile))
    data = json.load(gzip.open(datafile))
    # 读取数据集中的训练集，验证集和测试集
    train_set, val_set, eval_set = data

    # 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
    IMG_ROWS = 28
    IMG_COLS = 28
    # 根据输入mode参数决定使用训练集，验证集还是测试
    if mode == 'train':
        imgs = train_set[0]
        labels = train_set[1]
    elif mode == 'valid':
        imgs = val_set[0]
        labels = val_set[1]
    elif mode == 'eval':
        imgs = eval_set[0]
        labels = eval_set[1]
    # 获得所有图像的数量
    imgs_length = len(imgs)
    # 验证图像数量和标签数量是否一致
    assert len(imgs) == len(labels), \
          "length of train_imgs({}) should be the same as train_labels({})".format(
                  len(imgs), len(labels))

    index_list = list(range(imgs_length))

    # 读入数据时用到的batchsize
    BATCHSIZE = 100

    # 定义数据生成器
    def data_generator():
        # 训练模式下，打乱训练数据
        if mode == 'train':
            random.shuffle(index_list)
        imgs_list = []
        labels_list = []
        # 按照索引读取数据
        for i in index_list:
            # 读取图像和标签，转换其尺寸和类型
            img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
            label = np.reshape(labels[i], [1]).astype('int64')
            imgs_list.append(img) 
            labels_list.append(label)
            # 如果当前数据缓存达到了batch size，就返回一个批次数据
            if len(imgs_list) == BATCHSIZE:
                yield np.array(imgs_list), np.array(labels_list)
                # 清空数据缓存列表
                imgs_list = []
                labels_list = []

        # 如果剩余数据的数目小于BATCHSIZE，
        # 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
        if len(imgs_list) > 0:
            yield np.array(imgs_list), np.array(labels_list)

    return data_generator

# 定义模型结构
import paddle.nn.functional as F
from paddle.nn import Conv2D, MaxPool2D, Linear

# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):
     def __init__(self):
         super(MNIST, self).__init__()
         
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化核的大小kernel_size为2，池化步长为2
         self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化核的大小kernel_size为2，池化步长为2
         self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
         # 定义一层全连接层，输出维度是10
         self.fc = Linear(in_features=980, out_features=10)
         
   # 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出
   # 卷积层激活函数使用Relu，全连接层激活函数使用softmax
     def forward(self, inputs, label):
         x = self.conv1(inputs)
         x = F.relu(x)
         x = self.max_pool1(x)
         x = self.conv2(x)
         x = F.relu(x)
         x = self.max_pool2(x)
         x = paddle.reshape(x, [x.shape[0], 980])
         x = self.fc(x)
         if label is not None:
             acc = paddle.metric.accuracy(input=x, label=label)
             return x, acc
         else:
             return x

#调用加载数据的函数
train_loader = load_data('train')
    
#在使用GPU机器时，可以将use_gpu变量设置成True
use_gpu = True
paddle.set_device('gpu:0') if use_gpu else paddle.set_device('cpu')

#仅优化算法的设置有所差别
def train(model):
    model = MNIST()
    model.train()
    
    #四种优化算法的设置方案，可以逐一尝试效果
    # opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
    # opt = paddle.optimizer.Momentum(learning_rate=0.01, momentum=0.9, parameters=model.parameters())
    # opt = paddle.optimizer.Adagrad(learning_rate=0.01, parameters=model.parameters())
    opt = paddle.optimizer.Adam(learning_rate=0.01, parameters=model.parameters())
    
    EPOCH_NUM = 5
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            
            #前向计算的过程
            predicts, acc = model(images, labels)
            
            #计算损失，取一个批次样本损失的平均值
            loss = F.cross_entropy(predicts, labels)
            avg_loss = paddle.mean(loss)
            
            #每训练了100批次的数据，打印下当前Loss的情况
            if batch_id % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), acc.numpy()))
                
            #后向传播，更新参数，消除梯度的过程
            avg_loss.backward()
            opt.step()
            opt.clear_grad()

    #保存模型参数
    paddle.save(model.state_dict(), 'mnist.pdparams')
    
#创建模型    
model = MNIST()
#启动训练过程
train(model)

2 检查模型训练过程，识别潜在训练问题

使用飞桨动态图编程可以方便的查看和调试训练的执行过程。在网络定义的Forward函数中，可以打印每一层输入输出的尺寸，以及每层网络的参数。通过查看这些信息，不仅可以更好地理解训练的执行过程，还可以发现潜在问题，或者启发继续优化的思路。

在下述程序中，使用check_shape变量控制是否打印“尺寸”，验证网络结构是否正确。使用check_content变量控制是否打印“内容值”，验证数据分布是否合理。假如在训练中发现中间层的部分输出持续为0，说明该部分的网络结构设计存在问题，没有充分利用。

import paddle.nn.functional as F
# 定义模型结构
class MNIST(paddle.nn.Layer):
     def __init__(self):
         super(MNIST, self).__init__()
         
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化核的大小kernel_size为2，池化步长为2
         self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化核的大小kernel_size为2，池化步长为2
         self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
         # 定义一层全连接层，输出维度是10
         self.fc = Linear(in_features=980, out_features=10)
     
     #加入对每一层输入和输出的尺寸和数据内容的打印，根据check参数决策是否打印每层的参数和输出尺寸
     # 卷积层激活函数使用Relu，全连接层激活函数使用softmax
     def forward(self, inputs, label=None, check_shape=False, check_content=False):
         # 给不同层的输出不同命名，方便调试
         outputs1 = self.conv1(inputs)
         outputs2 = F.relu(outputs1)
         outputs3 = self.max_pool1(outputs2)
         outputs4 = self.conv2(outputs3)
         outputs5 = F.relu(outputs4)
         outputs6 = self.max_pool2(outputs5)
         outputs6 = paddle.reshape(outputs6, [outputs6.shape[0], -1])
         outputs7 = self.fc(outputs6)
         
         # 选择是否打印神经网络每层的参数尺寸和输出尺寸，验证网络结构是否设置正确
         if check_shape:
             # 打印每层网络设置的超参数-卷积核尺寸，卷积步长，卷积padding，池化核尺寸
             print("\n########## print network layer's superparams ##############")
             print("conv1-- kernel_size:{}, padding:{}, stride:{}".format(self.conv1.weight.shape, self.conv1._padding, self.conv1._stride))
             print("conv2-- kernel_size:{}, padding:{}, stride:{}".format(self.conv2.weight.shape, self.conv2._padding, self.conv2._stride))
             #print("max_pool1-- kernel_size:{}, padding:{}, stride:{}".format(self.max_pool1.pool_size, self.max_pool1.pool_stride, self.max_pool1._stride))
             #print("max_pool2-- kernel_size:{}, padding:{}, stride:{}".format(self.max_pool2.weight.shape, self.max_pool2._padding, self.max_pool2._stride))
             print("fc-- weight_size:{}, bias_size_{}".format(self.fc.weight.shape, self.fc.bias.shape))
             
             # 打印每层的输出尺寸
             print("\n########## print shape of features of every layer ###############")
             print("inputs_shape: {}".format(inputs.shape))
             print("outputs1_shape: {}".format(outputs1.shape))
             print("outputs2_shape: {}".format(outputs2.shape))
             print("outputs3_shape: {}".format(outputs3.shape))
             print("outputs4_shape: {}".format(outputs4.shape))
             print("outputs5_shape: {}".format(outputs5.shape))
             print("outputs6_shape: {}".format(outputs6.shape))
             print("outputs7_shape: {}".format(outputs7.shape))
             # print("outputs8_shape: {}".format(outputs8.shape))
             
         # 选择是否打印训练过程中的参数和输出内容，可用于训练过程中的调试
         if check_content:
            # 打印卷积层的参数-卷积核权重，权重参数较多，此处只打印部分参数
             print("\n########## print convolution layer's kernel ###############")
             print("conv1 params -- kernel weights:", self.conv1.weight[0][0])
             print("conv2 params -- kernel weights:", self.conv2.weight[0][0])

             # 创建随机数，随机打印某一个通道的输出值
             idx1 = np.random.randint(0, outputs1.shape[1])
             idx2 = np.random.randint(0, outputs4.shape[1])
             # 打印卷积-池化后的结果，仅打印batch中第一个图像对应的特征
             print("\nThe {}th channel of conv1 layer: ".format(idx1), outputs1[0][idx1])
             print("The {}th channel of conv2 layer: ".format(idx2), outputs4[0][idx2])
             print("The output of last layer:", outputs7[0], '\n')
            
        # 如果label不是None，则计算分类精度并返回
         if label is not None:
             acc = paddle.metric.accuracy(input=F.softmax(outputs7), label=label)
             return outputs7, acc
         else:
             return outputs7

#在使用GPU机器时，可以将use_gpu变量设置成True
use_gpu = True
paddle.set_device('gpu:0') if use_gpu else paddle.set_device('cpu')    

def train(model):
    model = MNIST()
    model.train()
    
    #四种优化算法的设置方案，可以逐一尝试效果
    opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
    # opt = paddle.optimizer.Momentum(learning_rate=0.01, momentum=0.9, parameters=model.parameters())
    # opt = paddle.optimizer.Adagrad(learning_rate=0.01, parameters=model.parameters())
    # opt = paddle.optimizer.Adam(learning_rate=0.01, parameters=model.parameters())
    
    EPOCH_NUM = 1
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，变得更加简洁
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            
            #前向计算的过程，同时拿到模型输出值和分类准确率
            if batch_id == 0 and epoch_id==0:
                # 打印模型参数和每层输出的尺寸
                predicts, acc = model(images, labels, check_shape=True, check_content=False)
            elif batch_id==401:
                # 打印模型参数和每层输出的值
                predicts, acc = model(images, labels, check_shape=False, check_content=True)
            else:
                predicts, acc = model(images, labels)
            
            #计算损失，取一个批次样本损失的平均值
            loss = F.cross_entropy(predicts, labels)
            avg_loss = paddle.mean(loss)
            
            #每训练了100批次的数据，打印下当前Loss的情况
            if batch_id % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), acc.numpy()))
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            opt.step()
            opt.clear_grad()

    #保存模型参数
    paddle.save(model.state_dict(), 'mnist_test.pdparams')
    
#创建模型    
model = MNIST()
#启动训练过程
train(model)

print("Model has been saved.")

3 加入校验或测试，更好评价模型效果

在训练过程中，我们会发现模型在训练样本集上的损失在不断减小。但这是否代表模型在未来的应用场景上依然有效？为了验证模型的有效性，通常将样本集合分成三份，训练集、校验集和测试集。

训练集 ：用于训练模型的参数，即训练过程中主要完成的工作。
校验集 ：用于对模型超参数的选择，比如网络结构的调整、正则化项权重的选择等。
测试集 ：用于模拟模型在应用后的真实效果。因为测试集没有参与任何模型优化或参数训练的工作，所以它对模型来说是完全未知的样本。在不以校验数据优化网络结构或模型超参数时，校验数据和测试数据的效果是类似的，均更真实的反映模型效果。

如下程序读取上一步训练保存的模型参数，读取校验数据集，并测试模型在校验数据集上的效果。

def evaluation(model):
    print('start evaluation .......')
    # 定义预测过程
    params_file_path = 'mnist.pdparams'
    # 加载模型参数
    param_dict = paddle.load(params_file_path)
    model.load_dict(param_dict)

    model.eval()
    eval_loader = load_data('eval')

    acc_set = []
    avg_loss_set = []
    for batch_id, data in enumerate(eval_loader()):
        images, labels = data
        images = paddle.to_tensor(images)
        labels = paddle.to_tensor(labels)
        predicts, acc = model(images, labels)
        loss = F.cross_entropy(input=predicts, label=labels)
        avg_loss = paddle.mean(loss)
        acc_set.append(float(acc.numpy()))
        avg_loss_set.append(float(avg_loss.numpy()))
    
    #计算多个batch的平均损失和准确率
    acc_val_mean = np.array(acc_set).mean()
    avg_loss_val_mean = np.array(avg_loss_set).mean()

    print('loss={}, acc={}'.format(avg_loss_val_mean, acc_val_mean))

model = MNIST()
evaluation(model)

从测试的效果来看，模型在验证集上依然有98.6%的准确率，证明它是有预测效果的。

4 加入正则化项，避免模型过拟合

1 过拟合现象

对于样本量有限、但需要使用强大模型的复杂任务，模型很容易出现过拟合的表现，即在训练集上的损失小，在验证集或测试集上的损失较大。

反之，如果模型在训练集和测试集上均损失较大，则称为欠拟合。过拟合表示模型过于敏感，学习到了训练数据中的一些误差，而这些误差并不是真实的泛化规律（可推广到测试集上的规律）。欠拟合表示模型还不够强大，还没有很好的拟合已知的训练样本，更别提测试样本了。因为欠拟合情况容易观察和解决，只要训练loss不够好，就不断使用更强大的模型即可，因此实际中我们更需要处理好过拟合的问题。

2 导致过拟合原因

造成过拟合的原因是模型过于敏感，而训练数据量太少或其中的噪音太多。

如图3 所示，理想的回归模型是一条坡度较缓的抛物线，欠拟合的模型只拟合出一条直线，显然没有捕捉到真实的规律，但过拟合的模型拟合出存在很多拐点的抛物线，显然是过于敏感，也没有正确表达真实规律。

如图4 所示，理想的分类模型是一条半圆形的曲线，欠拟合用直线作为分类边界，显然没有捕捉到真实的边界，但过拟合的模型拟合出很扭曲的分类边界，虽然对所有的训练数据正确分类，但对一些较为个例的样本所做出的妥协，高概率不是真实的规律。

3 过拟合的成因与防控

为了更好的理解过拟合的成因，可以参考侦探定位罪犯的案例逻辑，如图5 所示。

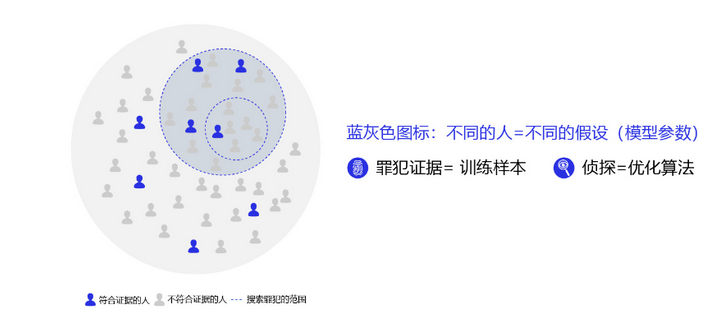
对于这个案例，假设侦探也会犯错，通过分析发现可能的原因：

情况1：罪犯证据存在错误，依据错误的证据寻找罪犯肯定是缘木求鱼。
情况2：搜索范围太大的同时证据太少，导致符合条件的候选（嫌疑人）太多，无法准确定位罪犯。

那么侦探解决这个问题的方法有两种：或者缩小搜索范围（比如假设该案件只能是熟人作案），或者寻找更多的证据。

归结到深度学习中，假设模型也会犯错，通过分析发现可能的原因：

情况1：训练数据存在噪音，导致模型学到了噪音，而不是真实规律。
情况2：使用强大模型（表示空间大）的同时训练数据太少，导致在训练数据上表现良好的候选假设太多，锁定了一个“虚假正确”的假设。

对于情况1，我们使用数据清洗和修正来解决。对于情况2，我们或者限制模型表示能力，或者收集更多的训练数据。

而清洗训练数据中的错误，或收集更多的训练数据往往是一句“正确的废话”，在任何时候我们都想获得更多更高质量的数据。在实际项目中，更快、更低成本可控制过拟合的方法，只有限制模型的表示能力。

4 正则化项

为了防止模型过拟合，在没有扩充样本量的可能下，只能降低模型的复杂度，可以通过限制参数的数量或可能取值（参数值尽量小）实现。

具体来说，在模型的优化目标（损失）中人为加入对参数规模的惩罚项。当参数越多或取值越大时，该惩罚项就越大。通过调整惩罚项的权重系数，可以使模型在“尽量减少训练损失”和“保持模型的泛化能力”之间取得平衡。泛化能力表示模型在没有见过的样本上依然有效。正则化项的存在，增加了模型在训练集上的损失。

飞桨支持为所有参数加上统一的正则化项，也支持为特定的参数添加正则化项。前者的实现如下代码所示，仅在优化器中设置weight_decay参数即可实现。使用参数coeff调节正则化项的权重，权重越大时，对模型复杂度的惩罚越高。

def train(model):
    model.train() 

    #各种优化算法均可以加入正则化项，避免过拟合，参数regularization_coeff调节正则化项的权重
    opt = paddle.optimizer.Adam(learning_rate=0.01, weight_decay=paddle.regularizer.L2Decay(coeff=1e-5), parameters=model.parameters())           

    EPOCH_NUM = 5
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，变得更加简洁
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            
            #前向计算的过程，同时拿到模型输出值和分类准确率
            predicts, acc = model(images, labels)
            #计算损失，取一个批次样本损失的平均值
            loss = F.cross_entropy(predicts, labels)
            avg_loss = paddle.mean(loss)
            
            #每训练了100批次的数据，打印下当前Loss的情况
            if batch_id % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), acc.numpy()))
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            opt.step()
            opt.clear_grad()

    #保存模型参数
    paddle.save(model.state_dict(), 'mnist_regul.pdparams')

model = MNIST()
train(model)

def evaluation(model):
    print('start evaluation .......')
    # 定义预测过程
    params_file_path = 'mnist_regul.pdparams'
    # 加载模型参数
    param_dict = paddle.load(params_file_path)
    model.load_dict(param_dict)

    model.eval()
    eval_loader = load_data('eval')

    acc_set = []
    avg_loss_set = []
    for batch_id, data in enumerate(eval_loader()):
        images, labels = data
        images = paddle.to_tensor(images)
        labels = paddle.to_tensor(labels)
        predicts, acc = model(images, labels)
        loss = F.cross_entropy(input=predicts, label=labels)
        avg_loss = paddle.mean(loss)
        acc_set.append(float(acc.numpy()))
        avg_loss_set.append(float(avg_loss.numpy()))
    
    #计算多个batch的平均损失和准确率
    acc_val_mean = np.array(acc_set).mean()
    avg_loss_val_mean = np.array(avg_loss_set).mean()

    print('loss={}, acc={}'.format(avg_loss_val_mean, acc_val_mean))

model = MNIST()
evaluation(model)

5 可视化分析

训练模型时，经常需要观察模型的评价指标，分析模型的优化过程，以确保训练是有效的。可选用这两种工具：Matplotlib库和VisualDL。

Matplotlib库：Matplotlib库是Python中使用的最多的2D图形绘图库，它有一套完全仿照MATLAB的函数形式的绘图接口，使用轻量级的PLT库（Matplotlib）作图是非常简单的。
VisualDL：如果期望使用更加专业的作图工具，可以尝试VisualDL，飞桨可视化分析工具。VisualDL能够有效地展示飞桨在运行过程中的计算图、各种指标变化趋势和数据信息。

1 使用Matplotlib库绘制损失随训练下降的曲线图

将训练的批次编号作为X轴坐标，该批次的训练损失作为Y轴坐标。

1 训练开始前，声明两个列表变量存储对应的批次编号(iters=[])和训练损失(losses=[])。

iters=[]
losses=[]
for epoch_id in range(EPOCH_NUM):
	"""start to training"""

2 随着训练的进行，将iter和losses两个列表填满。

import paddle.nn.functional as F

iters=[]
losses=[]
for epoch_id in range(EPOCH_NUM):
	for batch_id, data in enumerate(train_loader()):
        images, labels = data
        predicts, acc = model(images, labels)
        loss = F.cross_entropy(predicts, label = labels.astype('int64'))
        avg_loss = paddle.mean(loss)
        # 累计迭代次数和对应的loss
   	iters.append(batch_id + epoch_id*len(list(train_loader()))
	losses.append(avg_loss)

3 训练结束后，将两份数据以参数形式导入PLT的横纵坐标。

plt.xlabel("iter", fontsize=14)，plt.ylabel("loss", fontsize=14)

4 最后，调用plt.plot()函数即可完成作图。

plt.plot(iters, losses,color='red',label='train loss')

详细代码如下：

#引入matplotlib库
import matplotlib.pyplot as plt

def train(model):
    model.train()
    
    opt = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())
    
    EPOCH_NUM = 10
    iter=0
    iters=[]
    losses=[]
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，变得更加简洁
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            
            #前向计算的过程，同时拿到模型输出值和分类准确率
            predicts, acc = model(images, labels)
            #计算损失，取一个批次样本损失的平均值
            loss = F.cross_entropy(predicts, labels)
            avg_loss = paddle.mean(loss)
            
            #每训练了100批次的数据，打印下当前Loss的情况
            if batch_id % 100 == 0:
                print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), acc.numpy()))
                iters.append(iter)
                losses.append(avg_loss.numpy())
                iter = iter + 100
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            opt.step()
            opt.clear_grad()
            
    #保存模型参数
    paddle.save(model.state_dict(), 'mnist.pdparams')
    
    return iters, losses
    
model = MNIST()
iters, losses = train(model)

#画出训练过程中Loss的变化曲线
plt.figure()
plt.title("train loss", fontsize=24)
plt.xlabel("iter", fontsize=14)
plt.ylabel("loss", fontsize=14)
plt.plot(iters, losses,color='red',label='train loss') 
plt.grid()
plt.show()

2 使用VisualDL可视化分析

VisualDL是飞桨可视化分析工具，以丰富的图表呈现训练参数变化趋势、模型结构、数据样本、高维数据分布等。帮助用户清晰直观地理解深度学习模型训练过程及模型结构，进而实现高效的模型调优，具体代码实现如下。

步骤1：引入VisualDL库，定义作图数据存储位置（供第3步使用），本案例的路径是“log”。

from visualdl import LogWriter
log_writer = LogWriter("./log")

步骤2：在训练过程中插入作图语句。当每100个batch训练完成后，将当前损失作为一个新增的数据点(iter和acc的映射对)存储到第一步设置的文件中。使用变量iter记录下已经训练的批次数，作为作图的X轴坐标。

log_writer.add_scalar(tag = 'acc', step = iter, value = avg_acc.numpy())
log_writer.add_scalar(tag = 'loss', step = iter, value = avg_loss.numpy())
iter = iter + 100

# 安装VisualDL
!pip install --upgrade --pre visualdl

#引入VisualDL库，并设定保存作图数据的文件位置
from visualdl import LogWriter
log_writer = LogWriter(logdir="./log")

def train(model):
    model.train()
    
    opt = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())
    
    EPOCH_NUM = 10
    iter = 0
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，变得更加简洁
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            
            #前向计算的过程，同时拿到模型输出值和分类准确率
            predicts, avg_acc = model(images, labels)
            #计算损失，取一个批次样本损失的平均值
            loss = F.cross_entropy(predicts, labels)
            avg_loss = paddle.mean(loss)
            
            #每训练了100批次的数据，打印下当前Loss的情况
            if batch_id % 100 == 0:
                print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), avg_acc.numpy()))
                log_writer.add_scalar(tag = 'acc', step = iter, value = avg_acc.numpy())
                log_writer.add_scalar(tag = 'loss', step = iter, value = avg_loss.numpy())
                iter = iter + 100

            #后向传播，更新参数的过程
            avg_loss.backward()
            opt.step()
            opt.clear_grad()

    #保存模型参数
    paddle.save(model.state_dict(), 'mnist.pdparams')
    
model = MNIST()
train(model)

步骤3：命令行启动VisualDL。

使用“visualdl --logdir [数据文件所在文件夹路径] 的命令启动VisualDL。在VisualDL启动后，命令行会打印出可用浏览器查阅图形结果的网址。

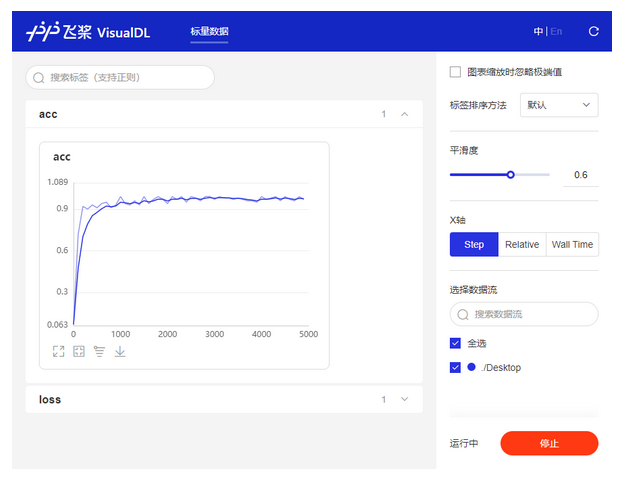
$ visualdl --logdir ./log --port 8080

步骤4：打开浏览器，查看作图结果，如图6 所示。

查阅的网址在第三步的启动命令后会打印出来（如http://127.0.0.1:8080/），将该网址输入浏览器地址栏刷新页面的效果如下图所示。除了右侧对数据点的作图外，左侧还有一个控制板，可以调整诸多作图的细节。

三模型加载和恢复训练

在快速入门中，我们已经介绍了将训练好的模型保存到磁盘文件的方法。应用程序可以随时加载模型，完成预测任务。但是在日常训练工作中我们会遇到一些突发情况，导致训练过程主动或被动的中断。如果训练一个模型需要花费几天的训练时间，中断后从初始状态重新训练是不可接受的。

万幸的是，飞桨支持从上一次保存状态开始训练，只要我们随时保存训练过程中的模型状态，就不用从初始状态重新训练。

下面介绍恢复训练的实现方法，依然使用手写数字识别的案例，网络定义的部分保持不变。

#数据处理部分之前的代码，保持不变
import os
import random
import paddle
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image

import gzip
import json
import warnings 
warnings.filterwarnings('ignore')

import paddle.nn as nn
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F

# 创建一个类MnistDataset，继承paddle.io.Dataset 这个类
# MnistDataset的作用和上面load_data()函数的作用相同，均是构建一个迭代器
class MnistDataset(paddle.io.Dataset):
    def __init__(self, mode):
        datafile = './work/mnist.json.gz'
        data = json.load(gzip.open(datafile))
        # 读取到的数据区分训练集，验证集，测试集
        train_set, val_set, eval_set = data
        
        # 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
        self.IMG_ROWS = 28
        self.IMG_COLS = 28

        if mode=='train':
            # 获得训练数据集
            imgs, labels = train_set[0], train_set[1]
        elif mode=='valid':
            # 获得验证数据集
            imgs, labels = val_set[0], val_set[1]
        elif mode=='eval':
            # 获得测试数据集
            imgs, labels = eval_set[0], eval_set[1]
        else:
            raise Exception("mode can only be one of ['train', 'valid', 'eval']")
        
        # 校验数据
        imgs_length = len(imgs)
        assert len(imgs) == len(labels), \
            "length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(labels))
        
        self.imgs = imgs
        self.labels = labels

    def __getitem__(self, idx):
        # MLP
        # img = np.array(self.imgs[idx]).astype('float32')
        # label = np.array(self.labels[idx]).astype('int64')
        # CNN
        img = np.reshape(self.imgs[idx], [1, self.IMG_ROWS, self.IMG_COLS]).astype('float32')
        label = np.reshape(self.labels[idx], [1]).astype('int64')

        return img, label

    def __len__(self):
        return len(self.imgs)

# 定义模型结构
class MNIST(paddle.nn.Layer):
     def __init__(self):
         super(MNIST, self).__init__()
         nn.initializer.set_global_initializer(nn.initializer.Uniform(), nn.initializer.Constant())
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化层卷积核kernel_size为2，池化步长为2
         self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化层卷积核kernel_size为2，池化步长为2
         self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
         # 定义一层全连接层，输出维度是10
         self.fc = Linear(in_features=980, out_features=10)
         
    # 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出
     def forward(self, inputs):
         x = self.conv1(inputs)
         x = F.relu(x)
         x = self.max_pool1(x)
         x = self.conv2(x)
         x = F.relu(x)
         x = self.max_pool2(x)
         x = paddle.reshape(x, [x.shape[0], 980])
         x = self.fc(x)
        #  x = F.softmax(x)
         return x

定义训练Trainer，包含训练过程和模型保存

class Trainer(object):
    def __init__(self, model_path, model, optimizer):
        self.model_path = model_path   # 模型存放路径 
        self.model = model             # 定义的模型
        self.optimizer = optimizer     # 优化器

    def save(self):
        # 保存模型
        paddle.save(self.model.state_dict(), self.model_path)

    def train_step(self, data):
        images, labels = data
        # 前向计算的过程
        predicts = self.model(images)
        # 计算损失
        loss = F.cross_entropy(predicts, labels)
        avg_loss = paddle.mean(loss)
        # 后向传播，更新参数的过程
        avg_loss.backward()
        self.optimizer.step()
        self.optimizer.clear_grad()
        return avg_loss

    def train_epoch(self, datasets, epoch):
        self.model.train()
        for batch_id, data in enumerate(datasets()):
            loss = self.train_step(data)
            # 每训练了1000批次的数据，打印下当前Loss的情况
            if batch_id % 500 == 0:
                print("epoch_id: {}, batch_id: {}, loss is: {}".format(epoch, batch_id, loss.numpy()))

    def train(self, train_datasets, start_epoch, end_epoch, save_path):
        if not os.path.exists(save_path):
            os.makedirs(save_path)
        for i in range(start_epoch, end_epoch):
            self.train_epoch(train_datasets, i)
            paddle.save(opt.state_dict(), './{}/mnist_epoch{}'.format(save_path,i)+'.pdopt')
            paddle.save(model.state_dict(), './{}/mnist_epoch{}'.format(save_path,i)+'.pdparams')
        self.save()

1 保存模型及参数，优化器参数

在开始介绍使用飞桨恢复训练前，先正常训练一个模型，优化器使用Adam，使用动态变化的学习率，学习率从0.01衰减到0.001。每训练一轮后保存一次模型，之后将采用其中某一轮的模型参数进行恢复训练，验证一次性训练和中断再恢复训练的模型表现是否相差不多（训练loss的变化）。

注意进行恢复训练的程序不仅要保存模型参数，还要保存优化器参数。这是因为某些优化器含有一些随着训练过程变换的参数，例如Adam、Adagrad等优化器采用可变学习率的策略，随着训练进行会逐渐减少学习率。这些优化器的参数对于恢复训练至关重要。

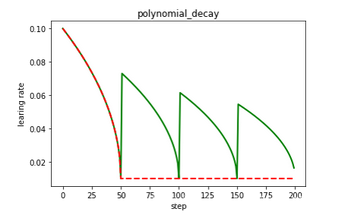
为了演示这个特性，训练程序使用PolynomialDecay API、Adam优化器、学习率以多项式曲线从0.01衰减到0.001。

参数说明如下：

learning_rate (float)：初始学习率，数据类型为Python float。
decay_steps (int)：进行衰减的步长，这个决定了衰减周期。
end_lr (float，可选）：最小的最终学习率，默认值为0.0001。
power (float，可选)：多项式的幂，默认值为1.0。
last_epoch (int，可选)：上一轮的轮数，重启训练时设置为上一轮的epoch数。默认值为-1，则为初始学习率。
verbose (bool，可选)：如果是 True，则在每一轮更新时在标准输出stdout输出一条信息，默认值为False。
cycle (bool，可选)：学习率下降后是否重新上升。若为True，则学习率衰减到最低学习率值时会重新上升。若为False，则学习率单调递减。默认值为False。

PolynomialDecay的变化曲线下图所示：

#在使用GPU机器时，可以将use_gpu变量设置成True
use_gpu = True
paddle.set_device('gpu:0') if use_gpu else paddle.set_device('cpu')

import warnings
warnings.filterwarnings('ignore')
paddle.seed(1024)


epochs = 3
BATCH_SIZE = 32
model_path = './mnist.pdparams'

train_dataset = MnistDataset(mode='train')
# 这里为了使每次的训练精度都保持一致，因此先选择了shuffle=False，真正训练时应改为shuffle=True
train_loader = paddle.io.DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=False, num_workers=0) 

model = MNIST()
# lr = 0.01
total_steps = (int(50000//BATCH_SIZE) + 1) * epochs
lr = paddle.optimizer.lr.PolynomialDecay(learning_rate=0.01, decay_steps=total_steps, end_lr=0.001)
opt = paddle.optimizer.Momentum(learning_rate=lr, parameters=model.parameters())

trainer = Trainer(
    model_path=model_path,
    model=model,
    optimizer=opt
)

trainer.train(train_datasets=train_loader, start_epoch = 0, end_epoch = epochs, save_path='checkpoint')

2 恢复训练

模型恢复训练，需要重新组网，所以我们需要重启AIStudio，运行MnistDataset数据读取和MNIST网络定义、Trainer部分代码，再执行模型恢复代码

在上述训练代码中，我们训练了五轮（epoch）。在每轮结束时，我们均保存了模型参数和优化器相关的参数。

使用model.state_dict()获取模型参数。
使用opt.state_dict获取优化器和学习率相关的参数。
调用paddle.save将参数保存到本地。

比如第一轮训练保存的文件是mnist_epoch0.pdparams，mnist_epoch0.pdopt，分别存储了模型参数和优化器参数。

使用paddle.load分别加载模型参数和优化器参数，如下代码所示。

paddle.load(params_path+'.pdparams')
paddle.load(params_path+'.pdopt')

如何判断模型是否准确的恢复训练呢？

理想的恢复训练是模型状态回到训练中断的时刻，恢复训练之后的梯度更新走向是和恢复训练前的梯度走向完全相同的。基于此，我们可以通过恢复训练后的损失变化，判断上述方法是否能准确的恢复训练。即从epoch 0结束时保存的模型参数和优化器状态恢复训练，校验其后训练的损失变化（epoch 1）是否和不中断时的训练相差不多。

说明：

恢复训练有如下两个要点：

保存模型时分别保存模型参数和优化器参数。
恢复参数时分别恢复模型参数和优化器参数。

下面的代码将展示恢复训练的过程，并验证恢复训练是否成功。加载模型参数并从第一个epoch开始训练，以便读者可以校验恢复训练后的损失变化。

import warnings
warnings.filterwarnings('ignore')
# MLP继续训练
paddle.seed(1024)

epochs = 3
BATCH_SIZE = 32
model_path = './mnist_retrain.pdparams'

train_dataset = MnistDataset(mode='train')
# 这里为了使每次的训练精度都保持一致，因此先选择了shuffle=False，真正训练时应改为shuffle=True
train_loader = paddle.io.DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=False, num_workers=4) 

model = MNIST()
# lr = 0.01
total_steps = (int(50000//BATCH_SIZE) + 1) * epochs
lr = paddle.optimizer.lr.PolynomialDecay(learning_rate=0.01, decay_steps=total_steps, end_lr=0.001)
opt = paddle.optimizer.Momentum(learning_rate=lr, parameters=model.parameters())

params_dict = paddle.load('./checkpoint/mnist_epoch0.pdparams')
opt_dict = paddle.load('./checkpoint/mnist_epoch0.pdopt')

# 加载参数到模型
model.set_state_dict(params_dict)
opt.set_state_dict(opt_dict)

trainer = Trainer(
    model_path=model_path,
    model=model,
    optimizer=opt
)
# 前面训练模型都保存了，这里save_path设置为新路径，实际训练中保存在同一目录就可以
trainer.train(train_datasets=train_loader,start_epoch = 1, end_epoch = epochs, save_path='checkpoint_con')

从恢复训练的损失变化来看，加载模型参数继续训练的损失函数值和正常训练损失函数值是相差不多的，可见使用飞桨实现恢复训练是极其简单的。总结一下：

保存模型时同时保存模型参数和优化器参数；

paddle.save(opt.state_dict(), 'model.pdopt')
paddle.save(model.state_dict(), 'model.pdparams')

恢复参数时同时恢复模型参数和优化器参数。

model_dict = paddle.load("model.pdparams")
opt_dict = paddle.load("model.pdopt")

model.set_state_dict(model_dict)
opt.set_state_dict(opt_dict)

paddle实现手写数字识别终章

一 资源配置

1 概述

前提条件

2 单GPU训练

2 分布式训练

1 模型并行

2 数据并行

1 PRC通信方式

2 NCCL2通信方式（Collective）

1. 基于launch方式启动

2. 基于spawn方式启动

二 训练调试和优化

1 计算模型的分类准确率

2 检查模型训练过程，识别潜在训练问题

3 加入校验或测试，更好评价模型效果

4 加入正则化项，避免模型过拟合

1 过拟合现象

2 导致过拟合原因

3 过拟合的成因与防控

4 正则化项

5 可视化分析

1 使用Matplotlib库绘制损失随训练下降的曲线图

2 使用VisualDL可视化分析

三 模型加载和恢复训练

1 保存模型及参数，优化器参数

2 恢复训练

相关文章

一资源配置

二训练调试和优化

三模型加载和恢复训练