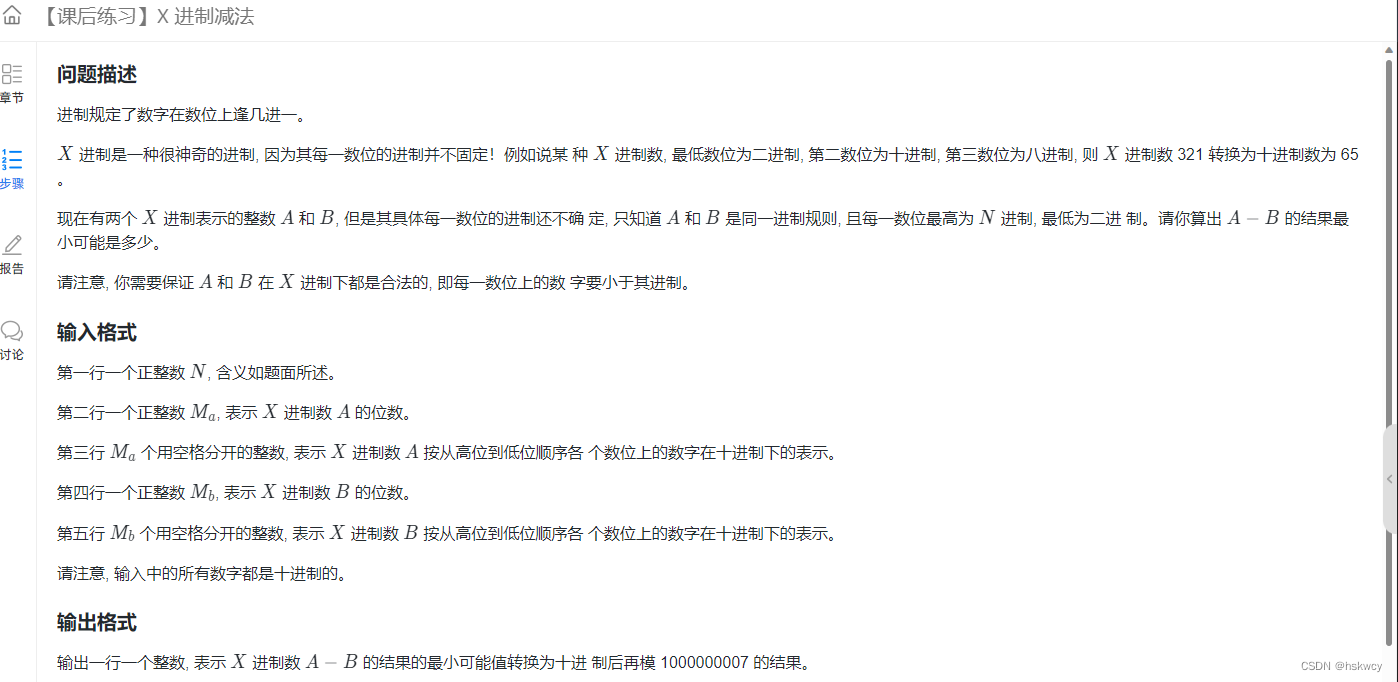
问题描述:
解题分析:
首先要搞明白 X 进制与 十 进制是如何转换的,以 X 进制321为例
题中说明,3 的进制为8,2的进制为10,1的进制为2
那么开始计算:
1就代表一个1
2的话是十进制,权值并不是10,而是2,因为只有低位满 2 时才会进1位,故此位所代表的数值转化为10进制为2*2=4
3的话是八进制,权值也不是8^2次方,而是10*2,因为只有最低位满2时,次低位才会进1,次低位只有满10时才会进1,故此位的权值为20,此位所代表的数值转化为10进制为20*3=60
三个位数代表的数值相加即为最后的10进制数,即为1+4+60=65
由以上分析可知一条最重要的原理就是
X 进制数的第 i 位的权值 = 低位进制之积
例如十进制中的百位的权值 = 10 *10 = 100
当搞明白X进制与十进制转化规则以后,来看题目:
题目意思是:两个不同位数的 X 进制数 A 和 B ,求每个位数的进制为多少时,A - B 的值最小,将结果对一个数取模输出;
首先要确定各个位数上的进制,因为进制数越大,表示的数也就越大,而题目要求两个数相减值最小,所以进制数越小越好,但是也不能无限制的小,进制数要比 A B 在该位数上的最大值大1,因为 M 进制所能表示的数的范围是 0 ~ M-1
其次为了防止在计算过程中,数据发生溢出,我们不能等到最后再对数取模输出,应该每处理一个位数的数据就对其进行处理
处理规则如下:
如果想求(5+6+7+8)% 6 的结果,为了防止数据溢出【当然这个数据不会溢出】
计算步骤应该为【(5%6)+(6%6)+(7%6)+(8%6)】%6 = 2
当然也可以写成【(5%6)+ (6%6)】% 6,拿这个结果加上(7%6),相加的结果再%6,依次相加即可,这样可以保证在数据相加的过程中,数据不会溢出
当然了,为了防止出现负数,可以使原数据加上 6 再对 6 取模,结果也是正确的,如下:
ans = ( 5 + 6 )% 6 = 5;ans =【 ans +( 7 + 6 )% 6 】% 6 = 0;
代码实现:
#include <bits/stdc++.h>
using namespace std;
const int vinf = 100010;
typedef long long ll;
int a[vinf]; //存放a的每个数位上的数值
int b[vinf];
int ans; //存放最后的结果
ll val[vinf]; //存储每个位数上的进制数
ll pro[vinf]; //计算每个位数的权值
const int pos = 1000000007;
int main(){
int N; //最大进制数
cin>>N;
int ma; //A的位数
cin>>ma;
for(int i=ma;i>=1;--i){
cin>>a[i];
}
int mb; //B的位数
cin>>mb;
for(int i=mb;i>=1;--i){
cin>>b[i];
}
//开始处理
int max_num = max(ma,mb); //取最大值,假如A有5位,B有四位,那么要处理5位数据
for(int i=1;i<=max_num;++i){
val[i] = max(max(a[i]+1,b[i]+1),2);
}
// int temp = 1;
// pro[1] = 1; //赋初值
// //用前缀积的方式计算每个位数的权值
// for(int i=2;i<=max_num;++i){
// temp *= val[i-1];
// pro[i] = temp;
// } //确定每一位上所占的权值,例如:题中例题321中的3,权值为pro[3] = 20;
// //开始正式计算A-B的值
// //包含计算每一位的数值(权值*当前数)以及取模操作
// for(int i=1;i<=max_num;++i){
// int ttemp = (a[i]-b[i])*pro[i];
// ttemp = (ttemp+pos)%pos; //确保每位的计算结果不为负数
// ans = (ans+ttemp)%pos; //确保ans永远比pos小
// }
//以上不可行,但是可以通过样例
for(int i=max_num;i>=2;--i){
ans = ((ans+a[i]-b[i])*val[i-1]) % pos;
}
ans += (a[1]-b[1]), ans %= pos;
cout<<ans<<endl;
return 0;
}
确定每一位的权值的思路不可行,可能是因为数据的问题【会溢出】
其实以上那个思路也可以,但是前提是要对每个位数的权值进行取模,别让数据太大,其次要比较a【i】与b【i】的大小,如果前者小的话,要向前借位;
改良版本:
#include <bits/stdc++.h>
using namespace std;
const int vinf = 100010;
typedef long long ll;
int a[vinf]; //存放a的每个数位上的数值
int b[vinf];
ll ans; //存放最后的结果
ll val[vinf]; //存储每个位数上的进制数
ll pro[vinf]; //计算每个位数的权值
const int pos = 1000000007;
int main(){
int N; //最大进制数
cin>>N;
int ma; //A的位数
cin>>ma;
for(int i=ma;i>=1;--i){
cin>>a[i];
}
int mb; //B的位数
cin>>mb;
for(int i=mb;i>=1;--i){
cin>>b[i];
}
//开始处理
int max_num = max(ma,mb); //取最大值,假如A有5位,B有四位,那么要处理5位数据
for(int i=1;i<=max_num;++i){
val[i] = max(max(a[i]+1,b[i]+1),2);
}
//包含计算每一位的数值(权值*当前数)以及取模操作
ll base=1;
for(int i=1;i<=max_num;++i){
if(a[i]>=b[i]){
ans += ((a[i]-b[i])*base)%pos;
}
else {
a[i+1]--;
a[i]+=val[i];
ans += ((a[i]-b[i])*base)%pos;
}
ans %= pos;
base *= val[i];
//base %= pos; //防止过大
}
cout<<ans<<endl;
return 0;
}
// //以上不可行,但是可以通过样例
// for(int i=max_num;i>=2;--i){
// ans = ((ans+a[i]-b[i])*val[i-1]) % pos;
// }
// ans += (a[1]-b[1]), ans %= pos;
思路二:
先将 A 与 B 的高位数字相减,乘以下一位的进制数,就是当前为所代表的的数值,然后拿着这个位的数值加上其他位的数值,但是在与其他位相加之前可以先取模,控制数据范围不让其溢出;
为了防止产生负数:还可以加上pos再取模!