【SVM分类】基于matlab哈里斯鹰算法优化支持向量机SVM分类【含Matlab源码 2243期】

news2025/1/21 1:00:39

⛄一、哈里斯鹰算法简介

HHO算法用数学公式来模拟现实中哈里斯鹰在不同机制下捕捉猎物的策略.在HHO中，哈里斯鹰是候选解，猎物随迭代逼近最优解.HHO算法包括两个阶段：全局探索阶段、局部开采阶段。
1 全局探索阶段
在这一阶段中，哈里斯鹰处于等待状态，仔细检查和监控搜索空间[lb,ub]以发现猎物.它根据两种策略在随机的地方寻找猎物，迭代时以概率q进行位置更新，数学表达式为：
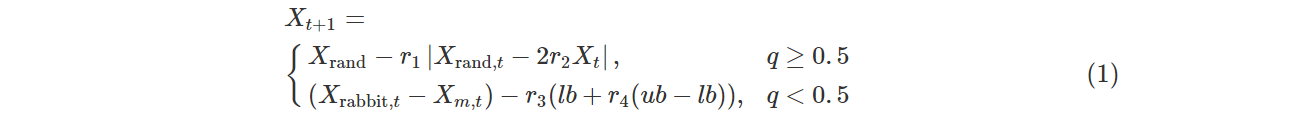
在这里插入图片描述
式中，Xt+1和Xt分别为哈里斯鹰第t+1次和第t次迭代时的位置，Xrabbit, t表示猎物第t次迭代时的位置，q和r1,r2,r3,r4是区间(0,1)内的随机数字，lb是搜索空间的下界，ub是搜索空间的上界，Xrand, t表示第t次迭代时哈里斯鹰的随机位置，Xm,t表示第t次迭代时哈里斯鹰的平均位置，公式如下：
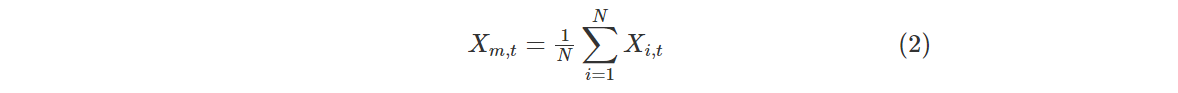
在这里插入图片描述
2 过渡阶段
任何群智能算法的精确运行，需要保持探索和开采之间适当的平衡.HHO通过猎物的能量方程实现从探索到开采的过渡，其模型如下：

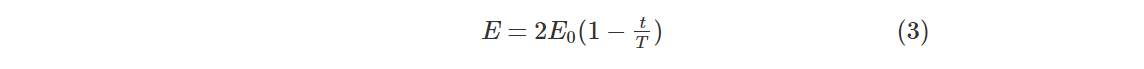
式中，E表示猎物逃跑的能量，E0是猎物能量的初始状态，公式为E0=2*rand-1,rand是(0,1)之间的随机数字，T为最大迭代次数，t为当前迭代次数.当|E|≥1时，哈里斯鹰算法将执行全局探索；否则，HHO算法进入局部开采.

3 局部开采阶段

在这一阶段，哈里斯鹰根据前一阶段的检测执行突袭攻击预期猎物，而猎物试图逃离危险.根据猎物的逃跑行为和哈里斯鹰的追逐策略，HHO算法提出了四种可能的策略来模拟攻击行为.用λ表示猎物成功逃脱的概率，当λ<0.5时，猎物逃脱成功；当λ≥0.5时，猎物逃脱失败.用参数E模拟哈里斯鹰软或硬的围攻策略.当|E|≥0.5时，执行软围攻；否则，执行硬围攻.
Case1:软围攻.当|E|≥0.5,λ≥0.5时，猎物有足够的能量且以跳跃的方式逃脱围捕，而哈里斯鹰会逐渐消耗猎物的能量，然后选择最佳的位置突袭俯冲逮捕猎物.更新位置的方程如下：
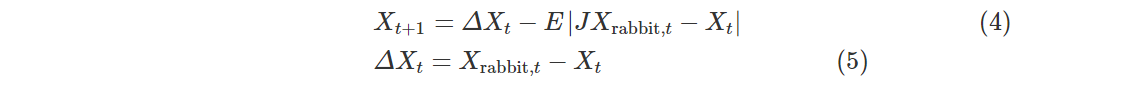
在这里插入图片描述
式中，Xt是迭代时猎物与哈里斯鹰的位置之差，J=2(1-r5)表示猎物逃跑过程中的随机跳跃，r5是介于0到1之间的随机数字.

Case2:硬围攻.当|E|<0.5,λ≥0.5时，猎物筋疲力尽，哈里斯鹰选择迅速突袭.位置更新如下：
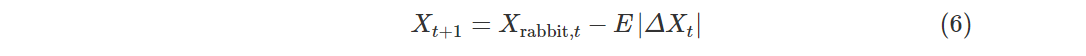
在这里插入图片描述
Case3:累速俯冲式软围攻.当|E|≥0.5,λ<0.5时，猎物有足够的能量E逃跑，哈里斯鹰在突袭之前会建立一个软围攻.为了模拟猎物的逃跑模式和跳跃动作，将levy函数LF集成在HHO算法中.更新位置的策略为：

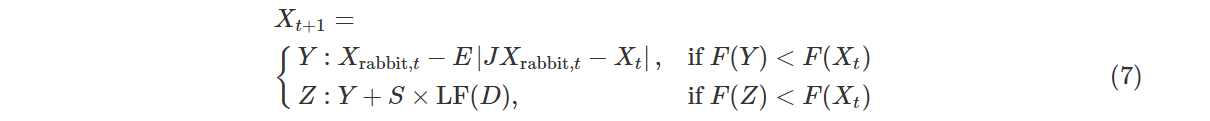
式中，D为问题维度，S为D维随机行向量.

Case4:累速俯冲式硬围攻.当|E|<0.5,λ<0.5时，猎物能量E低，哈里斯鹰在突袭前构建硬围攻捕捉猎物，位置更新如下：
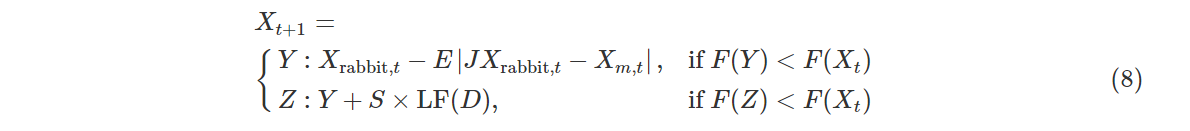
在这里插入图片描述
HHO算法用猎物能量E和因子λ调节哈里斯鹰和猎物(兔子)之间的四种围捕机制，来实现优化求解问题。

⛄二、部分源代码

clear all
clc
load wine
% load balance
% 选定训练集和测试集
% 将第一类的1-30,第二类的60-95,第三类的131-153做为训练集
train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)];
% 相应的训练集的标签也要分离出来
train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)];
% 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集
test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)];
% 相应的测试集的标签也要分离出来
test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)];
% 数据预处理
% 数据预处理,将训练集和测试集归一化到[0,1]区间
[mtrain,ntrain] = size(train_wine);
[mtest,ntest] = size(test_wine);
dataset = [train_wine;test_wine];

[dataset_scale,ps] = mapminmax(dataset’,0,1);
dataset_scale = dataset_scale’;

train_wine = dataset_scale(1:mtrain,:);
test_wine = dataset_scale( (mtrain+1):(mtrain+mtest),: );

Solution_no=20; %Number of search solutions
M_Iter=20; %Maximum number of iterations
LB = 0.01;
UB = 100;
F_obj = @(x)objfun(x,train_wine_labels,train_wine,test_wine_labels,test_wine);
Dim = 2;
[PIO_Best_FF,PIO_zbest,PIO_Conv_curve]=PIO(Solution_no,M_Iter,LB,UB,Dim,F_obj); % Call the AOA

bestc=PIO_zbest(1);
bestg=PIO_zbest(2);
disp(‘打印选择结果’);
str=sprintf(‘Best c = %g，Best g = %g’,bestc,bestg);
disp(str)
%% 利用最佳的参数进行SVM网络训练
cmd_gwosvm = ['-c ‘,num2str(bestc),’ -g ',num2str(bestg)];
model_gwosvm = svmtrain(train_wine_labels,train_wine,cmd_gwosvm);

%
%% SVM仿真测试
[predict_label_2,accuracy_2,bbb] = svmpredict(test_wine_labels,test_wine,model_gwosvm);
result_2 = [test_wine_labels predict_label_2];
total = length(test_wine_labels);
right = sum(predict_label_2 == test_wine_labels);
disp(‘打印测试集分类准确率’);
str = sprintf( ‘Accuracy = %g%% (%d/%d)’,accuracy_2(1),right,total);
disp(str);