文章目录
- 3D 变换
- 缩放(Scale)
- 平移(Translation)
- 旋转(Rotation)
- 3D 旋转(3D Rotation)
- 什么是欧拉角
- 罗德里格斯旋转公式(Rodrigues' Rotation Formula)
- Viewing transformation
- 什么是 View / Camera Transformation
- 相机标准位置(约定俗成)
- 怎样将一个相机从一个任意的摆放,放到一个标准位置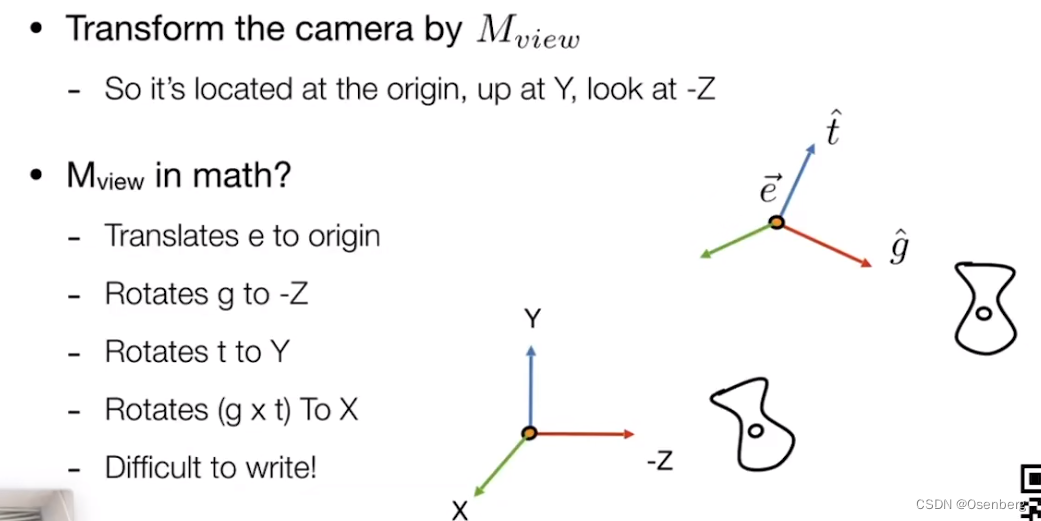
- 使用数学方式表示相机到标准位置的变换
- 投影变换(Projection Transformation)
- 正交投影和透视投影的区别
- 正交投影
- 正交投影的变换矩阵
- 透视投影(Perspective Projection)
- 怎样实现透视投影
- 计算透视投影的变换矩阵
3D 变换
同样引入齐次坐标:
- 3D 点 = ( x , y , z , 1 ) T (x, y, z, 1)^T (x,y,z,1)T
- 3D 向量 =
(
x
,
y
,
z
,
0
)
T
(x, y, z, 0)^T
(x,y,z,0)T
通常, ( x , y , z , w ) (x, y, z, w) (x,y,z,w)(w != 0) 表示一个坐标为 ( x / w , y / w , z / w ) (x/w, y/w, z/w) (x/w,y/w,z/w) 的 3D 点
用一个 4x4 的矩阵来表示 3D 的仿射变换
(
x
′
y
′
z
′
1
)
\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix}
⎝⎜⎜⎛x′y′z′1⎠⎟⎟⎞ =
(
a
b
c
t
x
d
e
f
t
y
g
h
i
t
z
0
0
0
1
)
\begin{pmatrix}a&b&c&t_x\\d&e&f&t_y\\g&h&i&t_z\\0&0&0&1\end{pmatrix}
⎝⎜⎜⎛adg0beh0cfi0txtytz1⎠⎟⎟⎞.
(
x
y
z
1
)
\begin{pmatrix}x\\y\\z\\1\end{pmatrix}
⎝⎜⎜⎛xyz1⎠⎟⎟⎞
2D/3D 变换中,是先做旋转(线性变换)再做平移
缩放(Scale)
S ( s x , s y , s z ) S(s_x, s_y, s_z) S(sx,sy,sz) = ( s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ) \begin{pmatrix}s_x&0&0&0\\0&s_y&0&0\\0&0&s_z&0\\0&0&0&1\end{pmatrix} ⎝⎜⎜⎛sx0000sy0000sz00001⎠⎟⎟⎞
平移(Translation)
T ( t x , t y , t z ) T(t_x, t_y, t_z) T(tx,ty,tz) = ( 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ) \begin{pmatrix}1&0&0&t_x\\0&1&0&t_y\\0&0&1&t_z\\0&0&0&1\end{pmatrix} ⎝⎜⎜⎛100001000010txtytz1⎠⎟⎟⎞
旋转(Rotation)
绕 x, y, z 三个轴分别做旋转的情况:
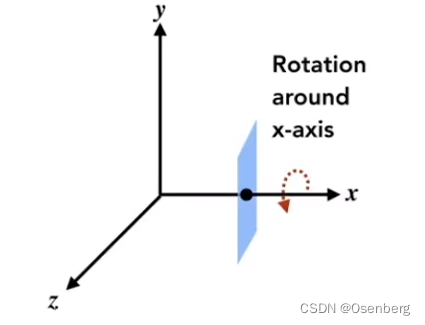
- 绕 X 轴旋转
R x ( α ) R_x(\alpha) Rx(α) = ( 1 0 0 0 0 c o s α − s i n α 0 0 s i n α c o s α 0 0 0 0 1 ) \begin{pmatrix}1&0&0&0\\0&cos\alpha&-sin\alpha&0\\0&sin\alpha&cos\alpha&0\\0&0&0&1\end{pmatrix} ⎝⎜⎜⎛10000cosαsinα00−sinαcosα00001⎠⎟⎟⎞ - 绕 Y 轴旋转
R y ( α ) R_y(\alpha) Ry(α) = ( c o s α 0 s i n α 0 0 1 0 0 − s i n α 0 c o s α 0 0 0 0 1 ) \begin{pmatrix}cos\alpha&0&sin\alpha&0\\0&1&0&0\\-sin\alpha&0&cos\alpha&0\\0&0&0&1\end{pmatrix} ⎝⎜⎜⎛cosα0−sinα00100sinα0cosα00001⎠⎟⎟⎞ - 绕 Z 轴旋转
R z ( α ) R_z(\alpha) Rz(α) = ( c o s α − s i n α 0 0 s i n α c o s α 0 0 0 0 1 0 0 0 0 1 ) \begin{pmatrix}cos\alpha&-sin\alpha&0&0\\sin\alpha&cos\alpha&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix} ⎝⎜⎜⎛cosαsinα00−sinαcosα0000100001⎠⎟⎟⎞
提示: R_y 中 − s i n α -sin\alpha −sinα 而 R_x 和 R_z 中是 s i n α sin\alpha sinα 的原因是, Y 轴是由 Z 叉乘 X 得到的,而不是 X 叉乘 Z(右手定则).
3D 旋转(3D Rotation)
任意的 3D 旋转都可以表示为绕 X Y Z 轴旋转的组合,公式如下
R
x
y
z
(
α
,
β
,
γ
)
R_{xyz}(\alpha,\beta,\gamma)
Rxyz(α,β,γ) =
R
x
(
α
)
R
y
(
β
)
R
z
(
γ
)
R_x(\alpha)R_y(\beta)R_z(\gamma)
Rx(α)Ry(β)Rz(γ)
什么是欧拉角
其中,
α
,
β
,
γ
\alpha, \beta, \gamma
α,β,γ 分别代表绕 X Y Z 三个轴旋转的角度,叫做欧拉角 (pitch, yaw, roll)
pitch 是围绕 X 轴旋转,也叫做俯仰角
yaw 是围绕 Y 轴旋转,也叫偏航角
roll 是围绕 Z 轴旋转,也叫翻滚角
罗德里格斯旋转公式(Rodrigues’ Rotation Formula)

Viewing transformation
这里的 Viewing transformation 包括 View(视图)/Camera 变换和 Projection(投影) 变换
投影变换包括: 正交(Orthographic)投影和透视(Perspective)投影
什么是 View / Camera Transformation
思考怎么拍一张照片?
- 找到一个合适的地方并且排列好拍照的人 (模型变换 Model Transformation)
- 找到一个合适的拍照角度放置相机 (视图变换 View Transformation)
- 拍照 (投影变换 Projection Transformation)
简称 MVP
怎么进行视图变换(View/Camera Transformation)?
首先定义相机的姿态(位置
e
⃗
\vec{e}
e,看的方向
g
^
\hat{g}
g^,向上方向(up direction,
t
^
\hat{t}
t^))
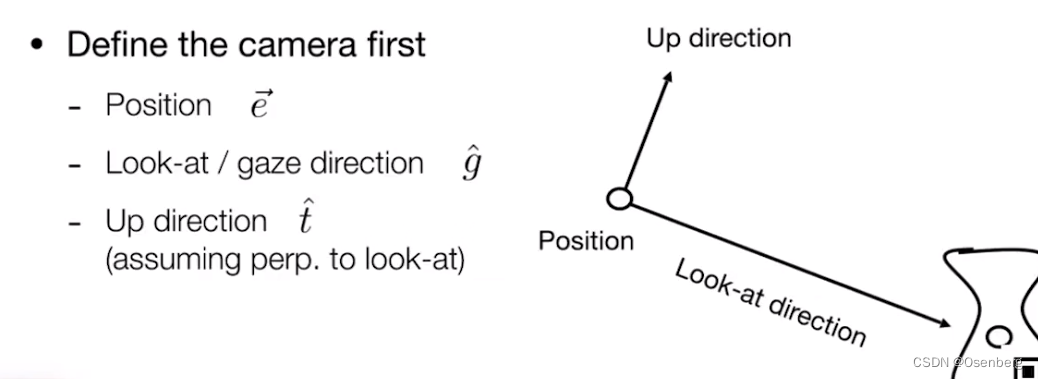
相机标准位置(约定俗成)
相机的位置为原点(0, 0, 0), Y 轴向上,看向 -Z,物体随着相机变换
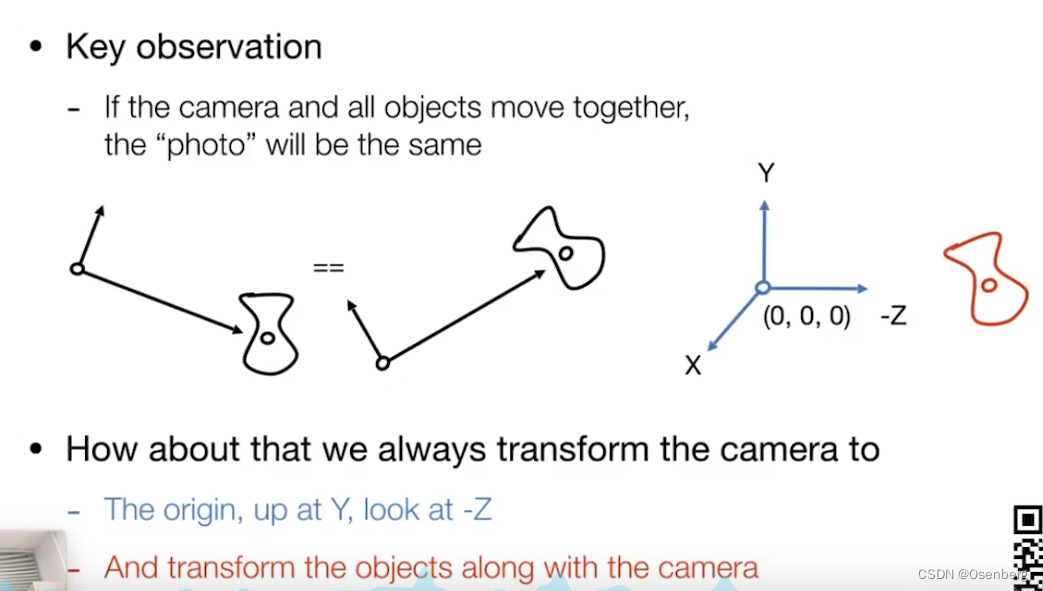
View Transformation 操作的是相机,其他物体跟着进行同样的变换
怎样将一个相机从一个任意的摆放,放到一个标准位置
- 将 e ⃗ \vec{e} e 平移到原点
- 将 g ^ \hat{g} g^ 旋转到 -Z
- t ^ \hat{t} t^ 旋转到 Y
- 旋转 ( g x t ) (g x t) (gxt) 到 X (注解: g 叉乘 t 得到 t ⃗ g ⃗ \vec{t} \vec{g} tg 坐标系的另一个轴)与 X 对应
使用数学方式表示相机到标准位置的变换

第一步,先做
e
⃗
\vec{e}
e 到原点的平移,
T
v
i
e
w
T_{view}
Tview 如图
第二部,因为计算从 g 到 -Z, t 到 Y, (g x t) 到 X 的旋转矩阵
R
v
i
e
w
R_{view}
Rview 比较困难,则先考虑 X 到 (g x t), Y 到 t, Z 到 -g,然后在求逆, 因为旋转矩阵就是一个正交矩阵,对求得旋转矩阵做一个转置,则可得到 g 到 -Z, t 到 Y, (g x t) 到 X 的旋转矩阵
R
v
i
e
w
R_{view}
Rview
相机按照此变换矩阵进行变换之后,相机内的物体都需按照此矩阵进行同样的变换。
View/Camera Transformation 是为了 Projection Transformation 做准备
投影变换(Projection Transformation)
前面说到投影变换分为正交投影(Orthographic Projection) 和透视投影(Perspective Projection)
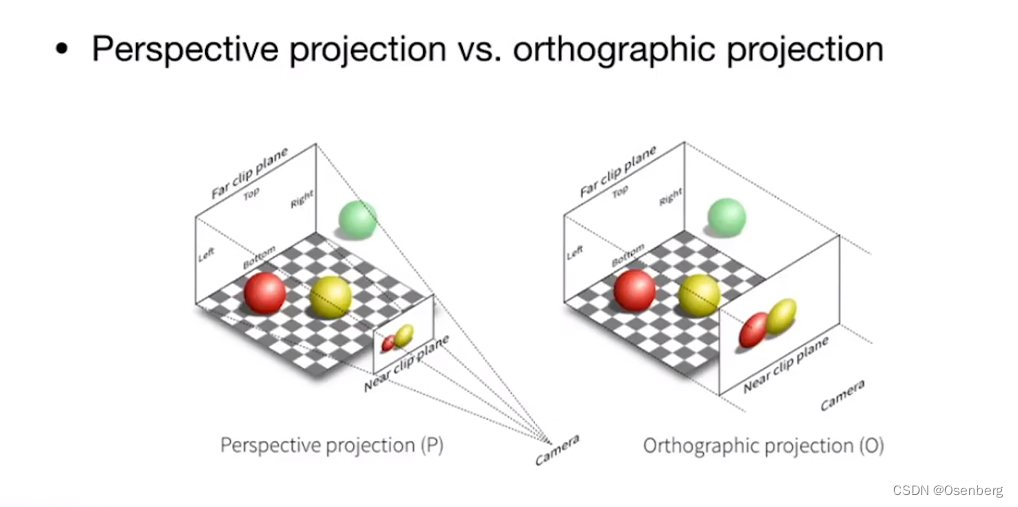
正交投影和透视投影的区别
正交投影, 不会给人带来近大远小的视觉(错觉),通常用在工程制图方面。
透视投影, 会给人带来近大远小的视觉(错觉)
正交投影
正交投影简单的理解/做法:
- 将相机放置在原点,看向 -Z,Y 是向上方向
- 那么如果直接将 Z 坐标直接扔掉,就可很方便的得到一个(x, y)二维平面的图形。
- 之后在将其平移和缩放到一个 [-1, 1] 的矩形内。
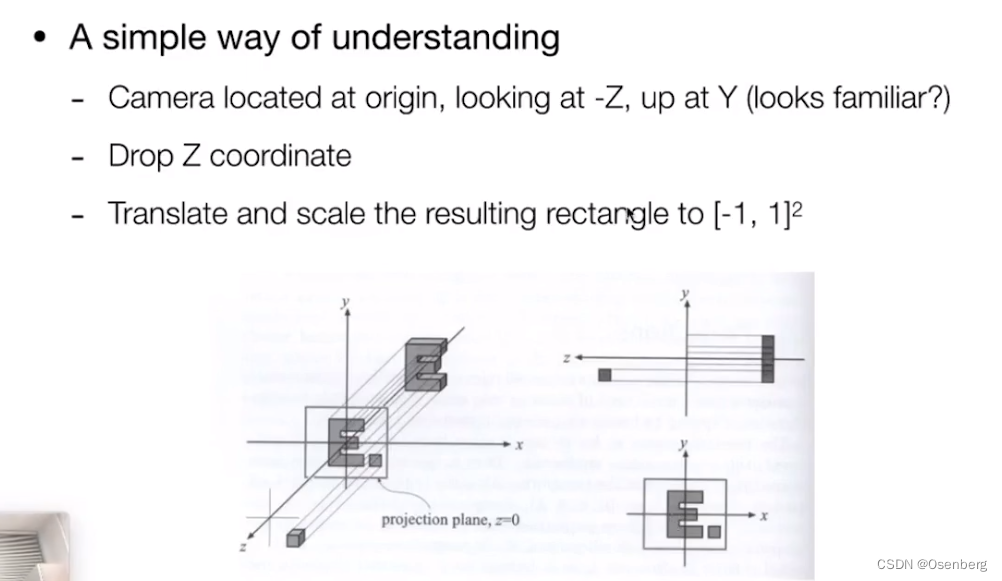
通常的做法:
将一个立方体的 [左(left), 右(right)] x [下(bottom), 上(top)] x [远(fast), 近(near)] 映射到一个 canonical 的立方体上 [ − 1 , 1 ] 3 [-1, 1]^3 [−1,1]3
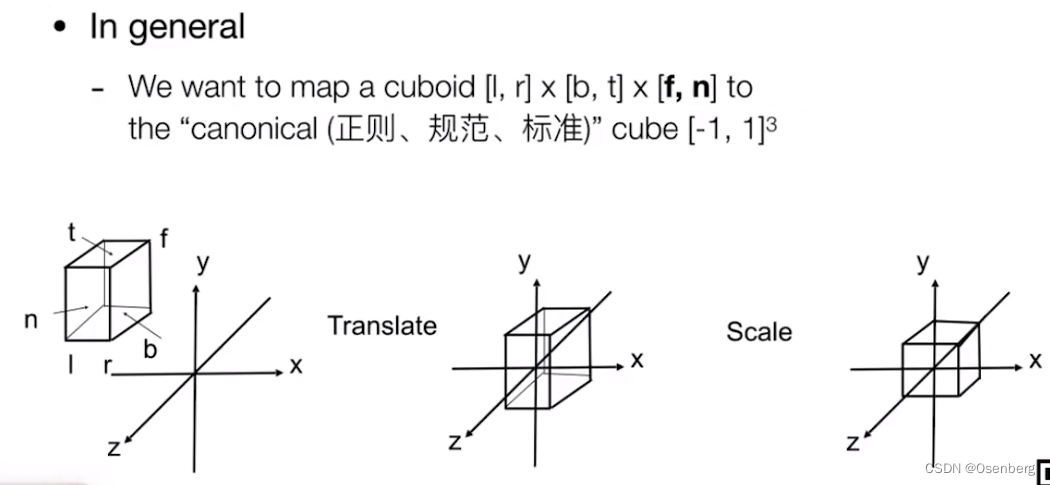
通常的做法与简单的做法的区别:
- 通过平移将立方体居中
- 通过缩放将立方体变为 “canonical” 立方体
此种情况下,对于 X 和 Y 都是 l, b 在 X, Y 轴的负半轴,r 和 t 在 X, Y 轴的正半轴, 则都是 r > l, t > b。而 f 在 Z 的负半轴(Camera 看向 -Z),n 在 Z 的正半轴,所以当立方体距离相机近的 n 的值是大于距离相机远的 f(正常应该是距离越远,值越大)。这也是 OpenGL 为什么使用左手系的原因.
正交投影的变换矩阵

2
r
−
l
\frac{2}{r-l}
r−l2 是将立方体的长度缩放到 [-1, 1] 的范围内,对于它的 Y 和 X 是同样的操作。
−
r
+
l
2
-\frac{r+l}{2}
−2r+l 是 X 轴的平移,对于它的 Y 和 X 是同样的操作
透视投影(Perspective Projection)
回顾一下齐次坐标的概念:
(
x
,
y
,
z
)
,
(
k
x
,
k
y
,
k
z
,
k
!
=
0
)
,
(
x
z
,
y
z
,
z
2
,
z
!
=
0
)
(x, y, z), (kx, ky, kz, k != 0), (xz, yz, z^2, z != 0)
(x,y,z),(kx,ky,kz,k!=0),(xz,yz,z2,z!=0) 都表示在 3D 空间中的同一个点
(
x
,
y
,
z
)
(x, y, z)
(x,y,z) 。
例如,
(
1
,
0
,
0
,
1
)
(1, 0, 0, 1)
(1,0,0,1) 和
(
2
,
0
,
0
,
2
)
(2, 0, 0, 2)
(2,0,0,2) 都表示
(
1
,
0
,
0
)
(1, 0, 0)
(1,0,0)
怎样实现透视投影
- 先将 Frustum 挤压称为一个长方体(n -> n, f -> f)( M p e r s p − > o r t h o M_{persp->ortho} Mpersp−>ortho)
- 然后做正交投影
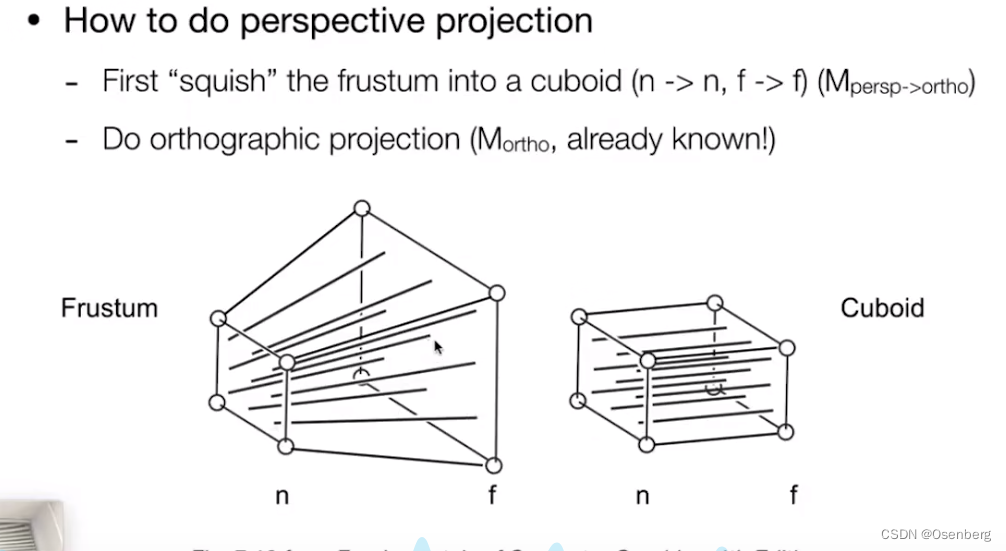
计算透视投影的变换矩阵
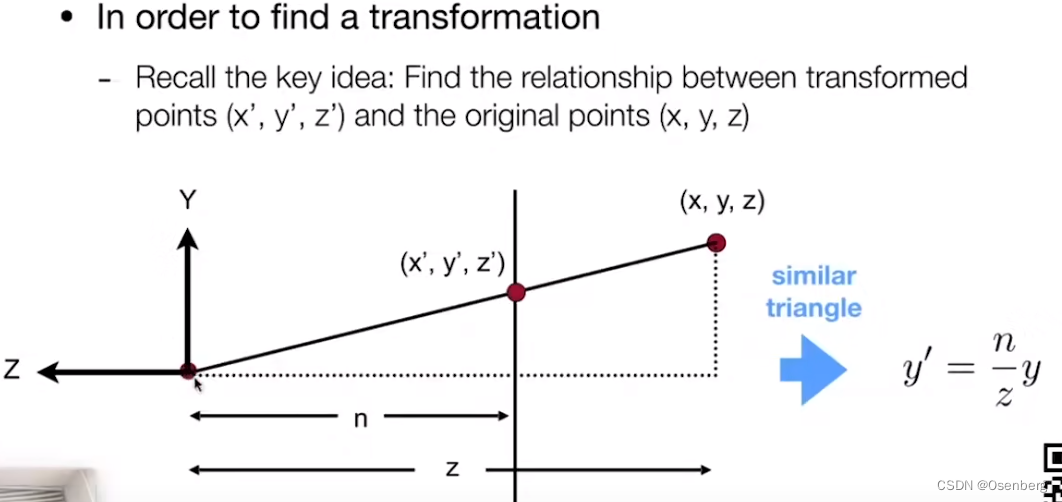
与
y
′
y'
y′ 类似的
x
′
=
n
z
x
x' = \frac{n}{z}x
x′=znx
那么在齐次坐标系中就有:






![[LeetCode周赛复盘] 第 92 场双周赛20221015](https://img-blog.csdnimg.cn/fe90b8cf343c48c7a75815560d3be358.png)