【图像处理】基于图像聚类的无监督图像排序问题（Matlab代码实现）

news2025/1/21 7:12:59

👨‍🎓个人主页：研学社的博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

本文的目标是近似解决被视为一种基于内容的图像聚类的无监督图像排序问题。基于内容的图像排序是创建一条路线，该路线一次遍历所有图像，其顺序是前一张图像中的下一个图像具有相似的内容。

最后，自动生成图像排序，以便具有相似内容的图像应该彼此接近。这个问题类似于文献中称为“旅行推销员问题”（TSP）的问题。已经提出了两类方法（最近邻法和遗传法），这些方法也已应用于TSP问题。

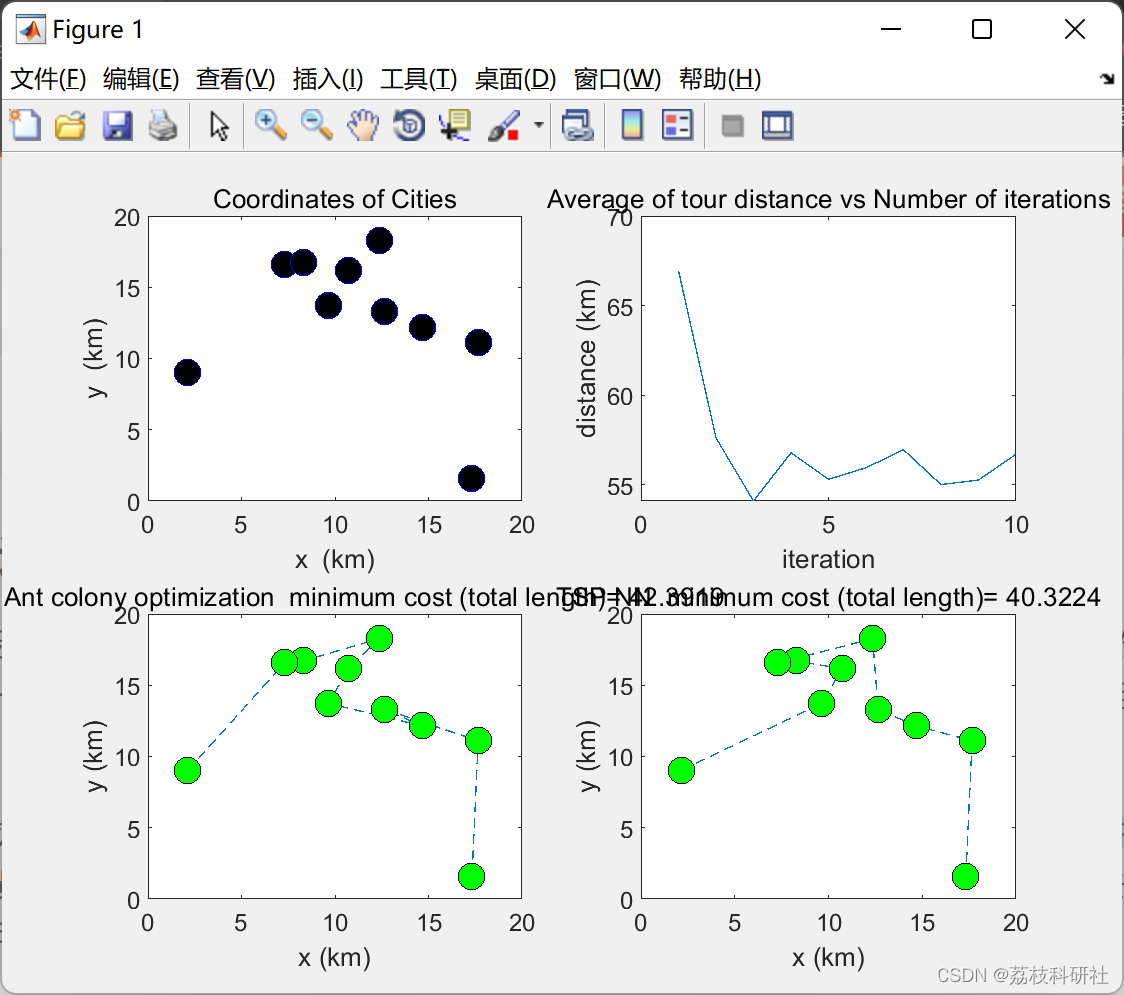
📚2 运行结果

部分代码：

clear all;
close all;

miter=10;

n=10;
m=3*n;
% parameters
e=.15; % evaporation coefficient.
alpha=1; % effect of ants' sight.
beta=4; % trace's effect.
t=0.0001*ones(n); % primary tracing.
el=.97; % common cost elimination.
% -------------------------------------------------------------------------
% Generate coordinates of cities and plot
for i=1:n
x(i)=rand*20;
y(i)=rand*20;
end
subplot(2,2,1);
plot(x,y,'o','MarkerFaceColor','k','MarkerEdgeColor','b','MarkerSize',10);
title('Coordinates of Cities');
xlabel('x (km)');
ylabel('y (km)');

% generating distace between cities matrix.
for i=1:n
for j=1:n
d(i,j)=sqrt((x(i)-x(j))^2+(y(i)-y(j))^2);
end
end

% generating sight matrix.
for i=1:n
for j=1:n
if d(i,j)==0
h(i,j)=0;
else
h(i,j)=1/d(i,j);
end
end
end
% ------------------------------------------------------------------------
% Main Algorithm: ACO Meta heuristic procedure
% a. Probabilistic solution construction biased by
% pheromone trails, without forward pheromone
% updating
% b. Deterministic backward path with loop elimination
% and with pheromone updating--> update_the_trace
% c. Evaluation of the quality of the solutions
% generated and use of the solution quality in
% determining the quantity of pheromone to deposit-->calculate_cost
% -------------------------------------------------------------------------
for i=1:miter
% Step 1: Forward ants and solution construction

% Generate places for each ant
for j=1:m
start_places(j,1)= rem(j-1,n)+1;%fix(1+rand*(n-1));
end
% Step 2:probabilistic solution contruction
[tour]=ant_tour(start_places,m,n,h,t,alpha,beta);
% tour=horzcat(tour,tour(:,1));

% Step 3: Calculate the cost --> total distace
[cost,f]=calculate_cost(m,n,d,tour,el);
[t]=update_the_trace(m,n,t,tour,f,e);
average_cost(i)=mean(cost);

% Step 4: Determine the best route
[min_cost(i),best_index]=min(cost);
besttour(i,:)=tour(best_index,:);
iteration(i)=i;
end
% -------------------------------------------------------------------------

% Plot Average of tour distance vs Number of Iterations
subplot(2,2,2);plot(iteration,average_cost);
title('Average of tour distance vs Number of iterations');
xlabel('iteration');
ylabel('distance (km)');

% Plot the best route
[k,l]=min(min_cost);
for i=1:n
X(i)=x(besttour(l,i));
Y(i)=y(besttour(l,i));
end
subplot(2,2,3);plot(X,Y,'--o',...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10)
xlabel('x (km)');ylabel('y (km)');
title(['TSP Ant colony optimization minimum cost (total length)= ',num2str(k)]);

[besttour,minCost] = getTSP_NN(d);

for i=1:n
X(i)=x(besttour(i));
Y(i)=y(besttour(i));
end
subplot(2,2,4);plot(X,Y,'--o',...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10)
xlabel('x (km)');ylabel('y (km)');
title(['TSP NN minimum cost (total length)= ',num2str(minCost)]);