F-二人的大富翁游戏
题目预览


题目背景(推荐阅读 题目预览)
如果遇到提交失败,请多次刷新,多次提交,会有成功几率
作为大学生,莲子和梅莉有着比高中时更为闲暇的课余时光。在没有课的时候,她们喜欢玩大富翁这一游戏,在游玩过程中交流自己的喜怒哀乐。
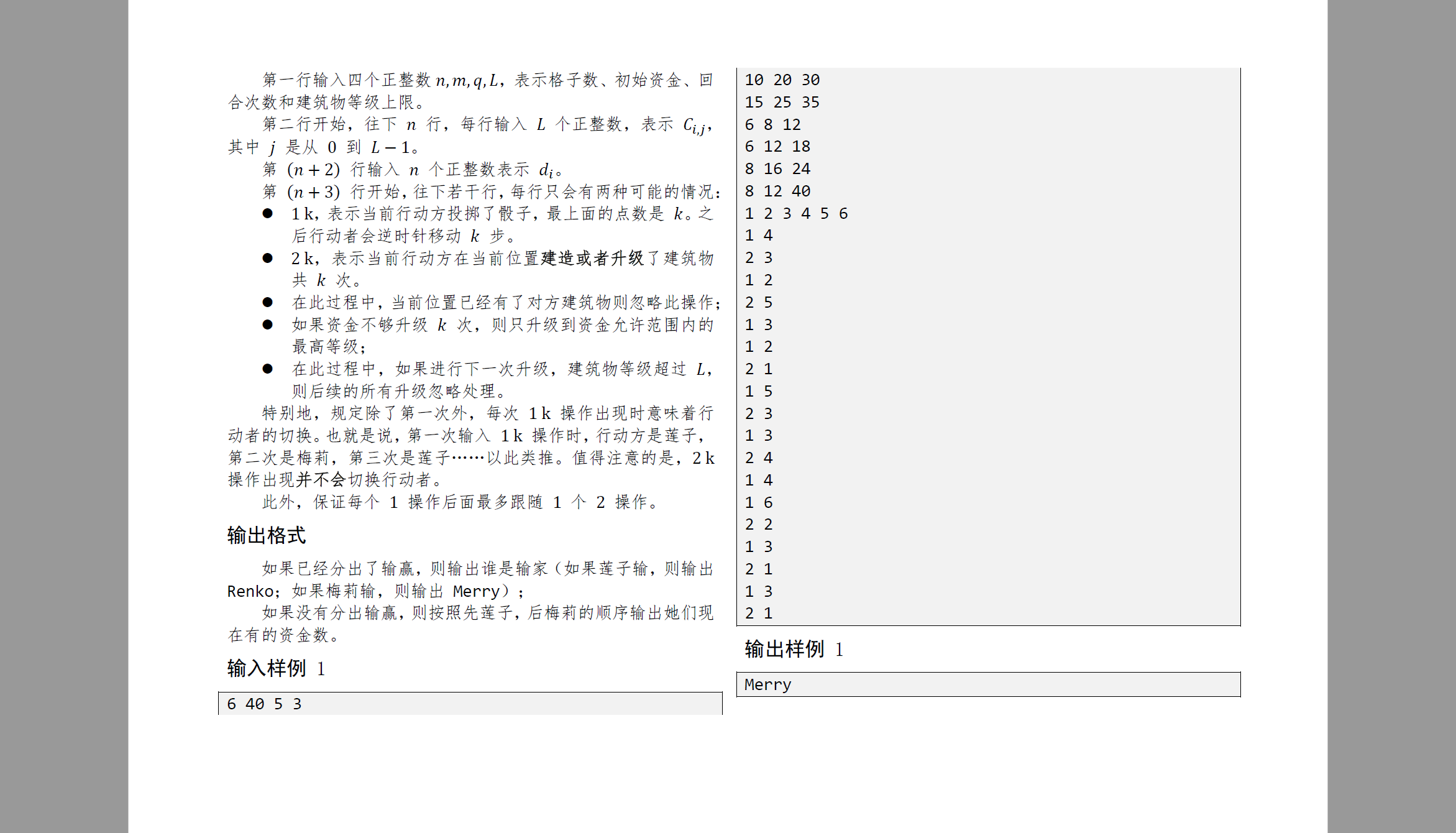
如图所示,是一个 n = 10 n=10 n=10 的大富翁地图。玩家在圆格子上行动。而方格子则可以建造建筑物。每个圆格子唯一对应一个方格子。
(友情提示:赌博是不对的)
题目描述
莲子和梅莉在玩大富翁游戏。这个大富翁游戏是由传智播客定制的,与一般的大富翁游戏在玩法上有略微区别,因此也被称为传智大富翁。
大富翁游戏是由 n n n 个格子组成,编号逆时针地从 1 , 2 , … , n 1,2,\dots,n 1,2,…,n,构成了一个环。莲子和梅莉起始在编号为 1 1 1 的格子。莲子和梅莉最开始都有 m m m 元资金。每一个回合,莲子先投掷骰子,再是梅莉投掷骰子。每一方行动时,设骰子最上面的数字为 k k k,则行动方逆时针移动 k k k 步。在移动的过程中,行动者所经过的每一个格子应当都分为两种情况:
- 如果当前格子(假设编号为 i i i)上有建筑物,而且建筑物是自己的,则行动方可以获得额外的 a i a_i ai 元资金。
- 如果当前格子上有建筑物,但是建筑物是对方的,则行动方要将自己的 a i a_i ai 元资金转移给对方。
在行动结束后亦有两种情况:
- 如果当前格子(设编号为 i i i)上没有建筑物,则行动方可以选择花费 C i , 0 C_{i,0} Ci,0 元资金(前提要求行动者当前的资金大于等于 C i , 0 C_{i,0} Ci,0)搭建建筑物,此时 a i a_i ai 被初始化为 C i , 0 C_{i,0} Ci,0。
- 如果当前格子的建筑物是行动方的,假设当前是一座 j j j 等级的建筑物,那么行动方可以选择用 C i , j C_{i,j} Ci,j 元为建筑物升级,功效是使得 a i ← a i + C i , j a_i \gets a_i+C_{i,j} ai←ai+Ci,j。这里, C i , j C_{i,j} Ci,j 表示将第 i i i 个格子上的第 j j j 等级的建筑物升级到第 j + 1 j+1 j+1 等级的建筑物所需花费的资金。同一回合内可以多次升级建筑。特别地,建筑物的等级上限为 L L L。如果当前建筑物等级已经到达上限则无法升级。
- 在所有建筑操作结束后,操作权转移给另一方。
两人都操作完一轮回合后,圆环上的每个建筑物都会提供给拥有者资金,具体来说,第 i i i 格上的建筑物会给其拥有者提供 d i d_i di 的资金。游戏结束当且仅当存在一个人在它行动过程中或者结束时的资金为负数。此时这个人成为输家(换而言之,允许中途过程资金为 0 0 0)。
给定莲子和梅莉的 q q q 个回合的每次操作,请问谁会是输家呢?
输入格式
第一行输入四个正整数 n , m , q , L n,m,q,L n,m,q,L,表示格子数、初始资金、回合次数和建筑物等级上限。
第二行开始,往下 n n n 行,每行输入 L L L 个正整数,表示 C i , j C_{i,j} Ci,j,其中 j j j 是从 0 0 0 到 L − 1 L-1 L−1。
第 ( n + 2 ) (n+2) (n+2) 行输入 n n n 个正整数表示 d i d_i di。
第 ( n + 3 ) (n+3) (n+3) 行开始,往下若干行,每行只会有两种可能的情况:
- 1 k \texttt{1 k} 1 k,表示当前行动方投掷了骰子,最上面的点数是 k k k。之后行动者会逆时针移动 k k k 步。
-
2
k
\texttt{2 k}
2 k,表示当前行动方在当前位置建造或者升级了建筑物共
k
k
k 次。
- 在此过程中,当前位置已经有了对方建筑物则忽略此操作;
- 如果资金不够升级 k k k 次,则只升级到资金允许范围内的最高等级;
- 在此过程中,如果进行下一次升级,建筑物等级超过 L L L,则后续的所有升级忽略处理。
特别地,规定除了第一次外,每次 1 k \texttt{1 k} 1 k 操作出现时意味着行动者的切换。也就是说,第一次输入 1 k \texttt{1 k} 1 k 操作时,行动方是莲子,第二次是梅莉,第三次是莲子……以此类推。值得注意的是, 2 k \texttt{2 k} 2 k 操作出现并不会切换行动者。
此外,保证每个 1 \bm 1 1 操作后面最多跟随 1 \bm 1 1 个 2 \bm 2 2 操作。
输出格式
如果已经分出了输赢,则输出谁是输家(如果莲子输,则输出 Renko \texttt{Renko} Renko;如果梅莉输,则输出 Merry \texttt{Merry} Merry);
如果没有分出输赢,则按照先莲子,后梅莉的顺序输出她们现在有的资金数。
样例 #1
样例输入 #1
6 40 5 3
10 20 30
15 25 35
6 8 12
6 12 18
8 16 24
8 12 40
1 2 3 4 5 6
1 4
2 3
1 2
2 5
1 3
1 2
2 1
1 5
2 3
1 3
2 4
1 4
1 6
2 2
1 3
2 1
1 3
2 1
样例输出 #1
Merry
样例 #2
样例输入 #2
6 9961 5 3
10 20 30
15 25 35
6 8 12
6 12 18
8 16 24
8 12 40
1 2 3 4 5 6
1 4
2 3
1 2
2 5
1 3
1 2
2 1
1 5
2 3
1 3
2 4
1 4
1 6
2 2
1 3
2 1
1 3
2 1
样例输出 #2
10099 9946
提示
【样例解释 1】
第一回合,莲子首先走
4
4
4 步,到达编号为
5
5
5 的格子,同时尝试建造与升级
3
3
3 次第五个格子的建筑物,但是
C
5
,
0
+
C
5
,
1
+
C
5
,
2
=
48
C_{5,0}+C_{5,1}+C_{5,2}=48
C5,0+C5,1+C5,2=48,所以只能把建筑物造到
2
2
2 级。此时莲子手上还有
16
16
16 元。
接着梅莉走了两步,到达编号为
3
3
3 的格子,同时尝试建造与升级
5
5
5 次第三个格子的建筑物,
C
3
,
0
+
C
3
,
1
+
C
3
,
2
=
26
C_{3,0}+C_{3,1}+C_{3,2}=26
C3,0+C3,1+C3,2=26,而造五次会超过等级上限
L
L
L,因此只能升到
3
3
3 次,此时梅莉手上还有
14
14
14 元。
回合结束后每个建筑物都会提供给拥有者
d
i
d_i
di 的资金,也就是说莲子此时手上有
21
21
21 元,梅莉手上有
17
17
17 元。
第二回合,莲子首先走
3
3
3 步,到达编号为
1
1
1 的格子。梅莉接着走
2
2
2 步,到达编号为
5
5
5 的格子,收取
a
i
a_i
ai 元。而
a
i
=
24
a_i=24
ai=24,因此梅莉的资金被扣成了负数,从而输出
Merry
\texttt{Merry}
Merry。
【样例解释 2】
仅在初始资金与第一组样例有一定变化,因此在这些回合中无法决出胜负,因此输出两人手上现有的资金。
【数据范围】
对于所有数据,保证 1 ≤ n , L ≤ 100 1 \leq n,L\leq 100 1≤n,L≤100, 1 ≤ q ≤ 1 0 4 1 \leq q \leq 10^4 1≤q≤104, 1 ≤ m , C i , j , d i ≤ 1 0 6 1 \leq m,C_{i,j},d_i \leq 10^6 1≤m,Ci,j,di≤106, 1 ≤ k ≤ 1 0 3 1 \leq k \leq 10^3 1≤k≤103(你可以不必在意怎么获得一个 k k k 面的骰子)。数据保证 1 1 1 操作次数恰好为 2 × q 2\times q 2×q。
题解

参考代码
-
版本1:
#include<bits/stdc++.h> #define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i) #define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i) using namespace std; typedef long long i64; const int INF = 2147483647; int qread(){ int w=1,c,ret; while((c = getchar()) > '9' || c < '0') w = (c == '-' ? -1 : 1); ret = c - '0'; while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0'; return ret * w; } int n, m, q, maxl; bool o = 1; const int MAXN = 100 + 3; int C[MAXN][MAXN], A[MAXN], D[MAXN], L[MAXN], O[3], T[MAXN]; i64 M[2]; int main(){ n = qread(), m = qread(), q = qread(), maxl = qread(); M[0] = M[1] = m, O[0] = O[1] = 1; up(1, n, i) L[i] = 0, T[i] = -1; up(1, n, i) up(0, maxl - 1, j) C[i][j] = qread(); up(1, n, i) D[i] = qread(); for(int op, k;~scanf("%d%d", &op, &k);){ if(op == 1){ if(o == 1){ up(1, n, i) if(T[i] != -1) M[T[i]] += D[i]; } o ^= 1; up(1, k, i){ O[o] = (O[o]) % n + 1; int p = O[o]; if(T[p] == o) M[o] += A[p]; else if(T[p] == !o){ M[!o] += A[p], M[o] -= A[p]; if(M[o] < 0) puts(o ? "Merry" : "Renko"), exit(0); } } } else { int p = O[o]; while(k && L[p] < maxl && M[o] >= C[p][L[p]] && T[p] != !o){ A[p] += C[p][L[p]], M[o] -= C[p][L[p]]; ++ L[p], T[p] = o, -- k; } } } up(1, n, i) if(T[i] != -1) M[T[i]] += D[i]; printf("%lld %lld\n", M[0], M[1]); return 0; } -
版本2:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <cctype> #include <queue> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();} while (isdigit(ch)){x=x*10+ch-48;ch=getchar();} return x*f; } int n,m,q,L,C[105][105],d[105],a[105],lv[105],pos[2],belong[105]; long long money[2]; const string name[2]={"Renko","Merry"}; inline void putfail(int id) { cout << name[id] << endl; exit(0); } inline void forward(int id,int k) { for (int i=1;i<=k;i++) { int &p=pos[id]; p++; if (p>n) p-=n; if (belong[p]==id) money[id]+=a[p]; else if (belong[p]==(id^1)) { money[id]-=a[p]; money[id^1]+=a[p]; } if (money[id]<0) putfail(id); } } inline void build(int id,int k) { int p=pos[id],cost=C[p][lv[p]]; for (int i=1;(money[id]>=cost && lv[p]<L && (belong[p]==-1 || belong[p]==id) && i<=k);i++) { belong[p]=id; money[id]-=cost; a[p]+=cost; cost=C[p][++lv[p]]; } } int main() { n=read(),m=read(),q=read(),L=read(); for (int i=1;i<=n;i++) { for (int j=0;j<L;j++) C[i][j]=read(); } for (int i=1;i<=n;i++) d[i]=read(); pos[0]=pos[1]=1; fill(belong+1,belong+n+1,-1); money[0]=money[1]=m; for (int i=0;i<2*q;i++) { int op=read(); begin: for (int j=1;j<=n && !(i&1);j++) { if (belong[j]==0) money[0]+=d[j]; else if (belong[j]==1) money[1]+=d[j]; } int k=read(); forward(i&1,k); if (i==2*q-1) break; op=read(); if (op==1) { i++; goto begin; } else { k=read(); build(i&1,k); } } for (int j=1;j<=n;j++) { if (belong[j]==0) money[0]+=d[j]; else if (belong[j]==1) money[1]+=d[j]; } cout << money[0] << " " << money[1] << endl; return 0; } { k=read(); build(i&1,k); } } for (int j=1;j<=n;j++) { if (belong[j]==0) money[0]+=d[j]; else if (belong[j]==1) money[1]+=d[j]; } cout << money[0] << " " << money[1] << endl; return 0; }













(数据库课设/软件工程大作业/软件工程课设)项目的创建、配置、说明文档与源码](https://img-blog.csdnimg.cn/0101126c55b64bd39d852d9dce9db3f9.png)