题目链接

F1. 生活在树上（easy version）

题目背景

本题是 B 组的最后一题，是 F2 题的简单版本，两道题目的解法略有不同。本题和 F2 题在题意上的区别在于本题给定树上的边权，而不是点权。

小智生活在「传智国」，这是一个有 $n$ 个城市的国家，各个城市由 $n-1$ 条道路相连。

每个道路都有长度 $w_i$ ，我们定义，小智从城市 $a$ 走到城市 $b$ 的代价是 ${\mathrm{d}\mathrm{i}\mathrm{s}}_{a,b}=\underset{e\in \mathrm{p}\mathrm{a}\mathrm{t}\mathrm{h}\left(a,b\right)}{⨁}{w}_e$，其中 $⨁$ 表示按位异或（如果你不知道什么是按位异或，请参见题目下方的提示/说明），$\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{h}\left(a,b\right)$ 表示 $a$ 到 $b$ 的简单路径上的边集。也即 ${\mathrm{d}\mathrm{i}\mathrm{s}}_{a,b}$ 表示将 $a$ 与 $b$ 的简单路径上所有边写作 $e_1,e_2,e_3,\dots$ 后，求 $w_{e_1}⨁w_{e_2}⨁w_{e_3}\dots$ 的结果。

有一天，小智获得了去参加传智杯的机会，他在前往比赛地的路上想到了一个问题，但他好像不会做，于是他把这个题告诉了你。聪明的同学，你可以帮帮他吗？

题目描述

小智说：「由于我们的国家只有 $n$ 个城市和 $n-1$ 条道路，那么我们的国家就相当于是一棵树。我在想，在我们的国家中，是否有城市满足『到城市 $a$ 的代价和到城市 $b$ 的代价的异或等于 $k$』。好难哦，我想不出来，你能帮帮我吗？」

形式化的，给定城市 $a,b$ 和整数 $k$，请你计算有哪几个城市 $t$ 满足 ${\mathrm{d}\mathrm{i}\mathrm{s}}_{t,a}⨁{\mathrm{d}\mathrm{i}\mathrm{s}}_{t,b}=k$。

输入格式

第一行有两个整数 $n$，$m$，表示国家的城市数和询问的个数。

接下来 $n-1$ 行，每行有两个整数 $x,y,l$，表示城市 $x$ 与城市 $y$ 有一条长度为 $l$ 的边。

接下来 $m$ 行，每行有三个整数 $a,b,k$，表示小智从城市 $a$ 走到城市 $b$，$k$ 的含义与题目描述一致。

输出格式

共 $m$ 行，每行一个整数。

对于第 $i$ 个询问，如果存在至少一个城市 $t$ 满足要求，则输出 Yes。

如果不存在任何一个城市满足条件，则输出 No。

输出字符串大小写不敏感，例如，Yes、yES、YES、yes 等都算作 Yes。

样例 #1

样例输入 #1

5 3
1 2 2
1 3 6 
2 4 8
2 5 1
1 2 4
2 3 12
1 4 10

样例输出 #1

nO
No
YeS

样例 #2

样例输入 #2

5 10
2 1 63
3 1 57
4 2 2
5 2 84
5 2 84
4 1 9977404983223574764
2 5 84
2 1 15996060349666123522
5 4 86
3 1 8428615422876116375
5 1 107
2 3 6
2 3 6
4 2 2

样例输出 #2

yeS
nO
YEs
No
YEs
nO
YEs
yeS
yeS
YEs

提示

相关概念解释

「树」：树是一个有 $n$ 个结点和 $n-1$ 条边的无向简单连通图。

「按位异或」：按位异或即 C++、python、java 语言中的 「^」 运算。它是一个二元运算，步骤是将两个数的二进制位按位比较，相同为 $0$，不同为 $1$。例如：$3⨁5=(011{)}_2⨁(101{)}_2=(110{)}_2=6$。请注意，这是一个按位运算，不是一个逻辑运算。

样例 1 解释

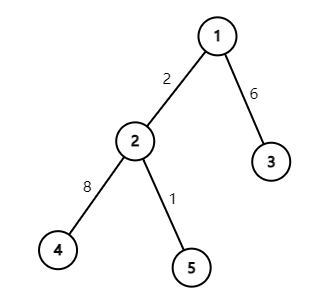
下图为传智国的地图。

∀ t ∈ { 1 , 2 , 3 , 4 , 5 } \forall t \in \{1, 2, 3, 4, 5\} ∀t∈{1,2,3,4,5}，都不可能有 ${\mathrm{d}\mathrm{i}\mathrm{s}}_{t,1}⨁{\mathrm{d}\mathrm{i}\mathrm{s}}_{t,2}=4$，${\mathrm{d}\mathrm{i}\mathrm{s}}_{t,2}⨁{\mathrm{d}\mathrm{i}\mathrm{s}}_{t,3}=12$，于是输出 No；

而取 $t=5$，有 ${\mathrm{d}\mathrm{i}\mathrm{s}}_{t,1}⨁{\mathrm{d}\mathrm{i}\mathrm{s}}_{t,4}=10$，于是输出 Yes。

数据规模与约定

对于所有测试点，保证 $1<n\le 5\times 10^5$，$1\le m\le 5\times 10^5$，$0\le w_i<2^{64}$。

对于每次询问，保证 $1\le a,b\le n$ 且 $a\ne b$，$0\le k<2^{64}$。
思路：
首先需要明确的是和异或的特点，两个相同的数异或的结果为0,任何数异或0之后的仍旧是它本身。所以这道题目，需要注意的就是树的存储方式。只要能选中任何一个点作为起点，计算完到其他n-1个点的异或的结果，就能知道是否满足给定的条件。
代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn=5e5+11;
#define ll unsigned long long 
int n,m;
ll dis[maxn];
bool flag[maxn];
struct edge
{
	int to;
	ll v;
};
vector<edge> e[maxn];
void dfs(int x)
{
	
	for(int i=0;i<e[x].size();i++)
	{
		ll y=e[x][i].to,z=e[x][i].v;
		if(flag[y]) continue;
		dis[y]=dis[x]^z;
		flag[y]=1;
		dfs(y);
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++)
	{
		int x,y;
		ll z;
		scanf("%d%d%llu",&x,&y,&z);
		e[x].push_back({y,z});
		e[y].push_back({x,z});
	}
	flag[1]=1;
	dfs(1);
	//for(int i=1;i<=n;i++) cout<<"i="<<i<<" "<<"dis[i]="<<dis[i]<<endl;
	for(int i=1;i<=m;i++)
	{
		int a,b;
		ll k;
		scanf("%d%d%llu",&a,&b,&k);
		//cout<<"dis[a]^dis[b="<<(dis[a]^dis[b])<<endl;
		if((dis[a]^dis[b])==k) printf("Yes\n");
		else printf("No\n");
	}
	return 0;
}