文章目录
- 一、寻找一个数(基本的二分搜索)
- 二、寻找左侧边界的二分搜索
- 三、寻找右侧边界的二分查找
- 总结
一、寻找一个数(基本的二分搜索)
这个场景是最简单的,可能也是大家最熟悉的,即搜索一个数,如果存在,返回其索引,否则返回 -1。
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
此算法有什么缺陷?
比如说给你有序数组 nums = [1,2,2,2,3],target 为 2,此算法返回的索引是 2,没错。但是如果我想得到 target 的左侧边界,即索引 1,或者我想得到 target 的右侧边界,即索引 3,这样的话此算法是无法处理的。
二、寻找左侧边界的二分搜索
以下是最常见的代码形式,其中的标记是需要注意的细节:
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0;
int right = nums.length; // 注意
while (left < right) { // 注意
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid; // 注意
}
}
return left;
}
-
为什么
while中是<而不是<=?答:用相同的方法分析,因为
right = nums.length而不是nums.length - 1。因此每次循环的「搜索区间」是[left, right)左闭右开。while(left < right)终止的条件是left == right,此时搜索区间[left, left)为空,所以可以正确终止。 -
为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办?
答:因为要一步一步来,先理解一下这个「左侧边界」有什么特殊含义:

,函数的返回值(即
left变量的值),表示的是小于target的值有多少个,取值区间是闭区间[0, nums.length],所以我们简单添加两行代码就能在正确的时候return -1:while (left < right) {
//…
}
// target 比所有数都大
if (left == nums.length) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1; -
为什么
left = mid + 1,right = mid ?和之前的算法不一样?答:这个很好解释,因为我们的「搜索区间」是
[left, right)左闭右开 -
为什么该算法能够搜索左侧边界?
关键在于对于
nums[mid] == target这种情况的处理:if (nums[mid] == target)
right = mid;
可见,找到 target 时不要立即返回,而是缩小「搜索区间」的上界 right,在区间 [left, mid) 中继续搜索,即不断向左收缩,达到锁定左侧边界的目的。
能不能想办法把 right 变成 nums.length - 1,也就是继续使用两边都闭的「搜索区间」?这样就可以和第一种二分搜索在某种程度上统一起来了。
要让搜索区间两端都闭,所以 right 应该初始化为 nums.length - 1,while 的终止条件应该是 left == right + 1,也就是其中应该用 <=:
int left_bound(int[] nums, int target) {
// 搜索区间为 [left, right]
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
// if else ...
}
因为搜索区间是两端都闭的,且现在是搜索左侧边界,所以 left 和 right 的更新逻辑如下:
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
由于 while 的退出条件是 left == right + 1,所以当 target 比 nums 中所有元素都大时,会存在以下情况使得索引越界:
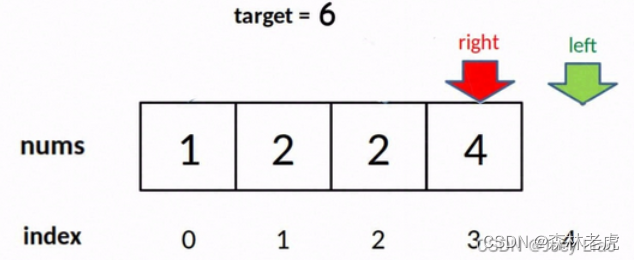
if (left >= nums.length || nums[left] != target)
return -1;
return left;
至此,整个算法就写完了,完整代码如下:
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// 搜索区间为 [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
}
// 检查出界情况
if (left >= nums.length || nums[left] != target) {
return -1;
}
return left;
三、寻找右侧边界的二分查找
类似寻找左侧边界的算法,这里也会提供两种写法,还是先写常见的左闭右开的写法,只有两处和搜索左侧边界不同
左闭右开
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
left = mid + 1; // 注意
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1; // 注意
}
左闭右闭
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 这里改成收缩左侧边界即可
left = mid + 1;
}
}
// 这里改为检查 right 越界的情况,见下图
if (right < 0 || nums[right] != target) {
return -1;
}
return right;
}
总结
两端都闭,普通情况,寻找左侧边界,寻找右侧边界
int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
// 最后要检查 left 越界的情况
if (left >= nums.length || nums[left] != target) {
return -1;
}
return left;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
// 最后要检查 right 越界的情况
if (right < 0 || nums[right] != target) {
return -1;
}
return right;
}