常用的密码算法有哪些？

我们将密码算法分为两大类。

对称密码（密钥密码）——算法只有一个密钥。如果多个参与者都知道该密钥，该密钥也称为共享密钥。
非对称密码（公钥密码）——参与者对密钥的可见性是非对称的。例如，一些参与者仅知道公钥，而另一些参与者同时知道公钥和私钥。

虽然对称密码和非对称密码并不是密码学中仅有的两类原语，但是由于我们很难对密码学的其他的子类进行划分，所以本书的大部分篇幅都是关于对称和非对称密码原语的。当今广泛应用的密码算法都包含在这两类原语中。另一种划分密码学原语的方式如下。

基于数学理论构造——这种密码算法的构造都建立在诸如因子分解之类的数学困难问题上。基于 RSA 算法的数字签名和非对称加密就属于这种构造。
基于启发式构造——这种算法的构造依赖于密码分析者的观察和统计分析。AES 算法就是这种构造的典型案例。

这种分类方式还考虑到算法效率因素，基于数学理论构造通常比基于启发式构造的密码算法要慢得多。我们可以得出这样的结论：对称密码大多数都是基于启发式构造的，而非对称密码主要是基于数学理论构造的。

我们很难严格地对密码学涉及的所有算法进行准确分类。事实上，每本书或每门课程对密码学定义和分类都有所不同。其实，这些定义和分类对我们来说并不重要，因为我们只会将这些密码学原语看作独特且具有各自的安全声明的工具。反过来，我们可以把这些工具当作构造安全协议的基础原语。对于实现协议安全，了解这些工具的工作原理以及提供的安全声明才是重中之重。出于这种考虑，本书的第一部分主要介绍常用的密码原语及其安全属性。

本书中的许多概念在初次使用时可能比较难懂。但与学习和理解其他知识一样，对这些概念了解得越多，在具体语境中见到的次数越多，我们就越能把它们抽象出来，理解起来也就愈加自然。本书的作用就是帮助读者建立起密码算法构造的抽象思维模型，理解把各类密码算法组合在一起形成安全协议的方法。本书会反复提到各类密码原语构造的接口，给出它们在现实世界的实际使用示例。

密码学以前的定义很简单，其原理类似于 Alice 和 Bob 想要交换秘密信息。当然，现在密码学的定义已经有了变化。当今，密码学围绕着新的发现、突破和实际需求演变成一门非常复杂的学科。归根结底，密码学的真正目的在于增强协议安全性，使协议在敌手存在的情况下仍能安全运行。

为了准确地理解密码学使协议变得安全的原理，厘清协议所要达到的一系列安全目标至关重要。本书涉及的密码原语至少满足下面性质中的一条。

机密性——掩藏和保护一些不想让别人看到的消息。例如，加密就可以掩盖传输中的消息。
认证性——确定通信另一方的身份。例如，认证技术可以让我们确信接收到的消息确实是由 Alice 发送来的。

当然，这里只是对密码学所能提供的算法功能进行了简化。在大多数情况下，每个密码原语的安全定义中都包含对算法功能的详细说明。密码原语的使用方式不同，协议产生的安全属性也会不同。

在本书中，我们将会学习一些新的密码原语，同时还会学习将它们组合起来实现满足机密性或认证性等安全属性的方法。请认识到这样一个事实：密码学是一门在敌手存在的环境下为协议提供安全保护的技术。虽然本书对“敌手”还没给出明确的定义，但是我们可以把企图破坏协议的参与者、观察者、中间人都当作敌手。这些角色反映了现实生活中敌手可能的身份。毕竟，密码学是一个实用的领域，它最终对抗的坏人是有血有肉的。

对称密码：对称加密概述

对称加密（Symmetric Encryption）是密码学的重要概念之一。对称密码在密码学中有着举足轻重的地位，本书中的大多数密码算法或协议都用到对称密码。现在，我们借助将要介绍的第一个协议引入对称加密这个新概念。想象这样一个情景：Alice 需要给住在城堡外的 Bob 寄送一封信件。如图 1.1 所示，Alice 要求她忠实的信使（Messenger）骑上他的骏马，穿越前方危险的土地，向 Bob 传递重要消息。然而，Alice 对信使很是怀疑；尽管这位忠实的信使为她效劳多年，但她仍希望此次传递的消息对包括信使在内的所有被动观察者均保密。试想一下，这封信可能包含一些关于王国的流言蜚语。

Alice 需要的是一个协议，它能模拟 Alice 亲自将消息传递给 Bob 的过程。这是一个在现实中不可能解决的问题，除非我们采用密码学（或隐形传输）技术。这就要用到密码学家多年前发明的一种新型加密算法，常称为对称加密算法（Symmetric Encryption Algorithm）。

注意：

顺便说一下，密码学算法通常也被称为密码学原语。我们可以将密码学原语视为密码学中一种最小的算法构造，它通常与其他原语一起用于构造新的协议。“密码学原语”一词经常出现在相关文献中，了解它有利于阅读文献，但它本身确实没有特别的意义，仅仅是一个新的术语而已。

接下来，让我们看看如何使用这个对称加密算法向信使隐藏 Alice 的真实消息。现在，假设这个密码学原语是一个提供了以下两个函数的黑盒子（我们无法看到它的内部构造）。

ENCRYPT；
DECRYPT 。

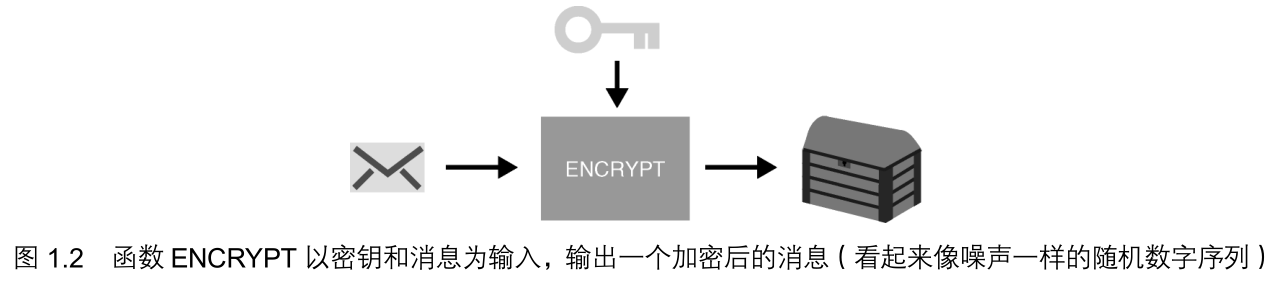
第一个函数 ENCRYPT 以密钥（Secret Key）和消息（Message）为输入，它输出一系列看起来像是随机选择的数字，如果我们愿意的话，它也可以输出像噪声一样的数据。我们把这个函数的输出称为加密消息。函数 ENCRYPT 的原理如图 1.2 所示。

第二个函数 DECRYPT 是第一个函数 ENCRYPT 的逆函数，它以 ENCRYPT 输入的密钥和输出的加密消息为输入，输出原始消息。函数 DECRYPT 的原理如图 1.3 所示。

为了使用这个新的密码学原语，Alice 和 Bob 不得不在现实世界中先会面一次，商定他们将要使用的密钥。之后，Alice 可以使用商定的密钥和函数 ENCRYPT 去保护她的消息。接着，她将加密的消息交给信使，并由信使转交给 Bob 。Bob 收到加密的消息后，使用与 Alice 相同的密钥和函数 DECRYPT 恢复出原始消息。具体过程如图 1.4 所示。

在该消息传递过程中，信使拥有的都是看起来随机的消息，这不会对他获得隐藏的消息提供任何有意义的帮助。借助密码学技术，我们有效地将不安全的协议转变为安全协议。新协议使得 Alice 可以在没有任何人（除 Bob 外）知道消息内容的情况下向 Bob 传递一封机密信件。

在密码学中，使一个协议变得安全的常见做法就是：使用密钥将消息转变成噪声，使经过变换后的消息与随机数字序列无法区分开来。在接下来的章节中，我们将通过学习更多的密码算法来了解这个过程。

顺便说一句，对称加密是对称密码（Symmetric Cryptography）或密钥密码（Secret Key Cryptography）的一部分。此类密码学原语的不同函数往往使用相同的密钥。在后面的章节中，我们还会看到密钥有时不止一个。

非对称加密：两个密钥优于一个密钥

在前面关于对称加密的讨论中，我们曾提到：Alice 和 Bob 在安全传递信件前需要见面，以确定他们将要使用的对称加密密钥。这是一个合理的要求，许多协议实际上都有这样的前提要求。然而，这样的要求在有许多参与者的协议中很快变得不那么实用：在安全连接到谷歌、Facebook 、亚马逊和其他数十亿网站之前，网络浏览器是否也要满足这样的要求（即在连接前，浏览器之间要相互确定使用的对称加密密钥）？

这也称为密钥分发问题，在相当长的一段时间内该问题都未被解决，直到 20 世纪 70 年代末密码学家发现了另一类称为非对称密码（Asymmetric Cryptography）或公钥密码（Public Key Cryptography）的算法，密钥分发问题才得以解决。在非对称密码中，不同的函数（ENCRYPT 和 DECRYPT ）使用不同的密钥（对称密码仅使用单个密钥）。为了说明公钥密码如何帮助人们建立信任，我将在本节介绍一些非对称密码原语。注意，这些原语只是本书内容的概览，在后续章节中我们会更详细地讨论这些密码原语。

以上内容来自《深入浅出密码学》