3.5.2 基于伪随机函数的CPA安全

基于伪随机函数的加密示意图

CONSTRUCTION 3.28 构造基于伪随机函数的CPA安全的加密方案

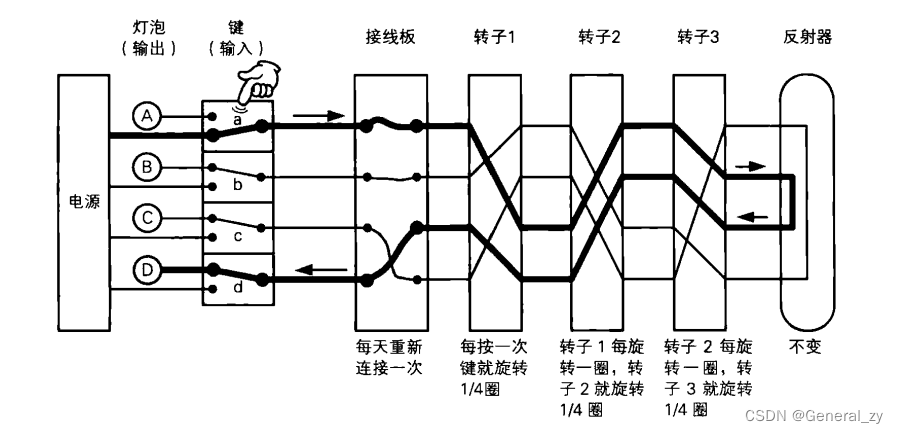
设F是一个伪随机函数，则定义一个对于明文长度为 n 的私钥加密方案如下：

Gen：对于输入1^n，随机均匀选择 k ∈ {0, 1}^n 并输出

Enc：对于输入的 k ∈ {0, 1}^n以及明文 m ∈ {0, 1}^n，随机均匀选择 r∈{0, 1}^n，然后输出密文c := <r, s>，其中 s=Fk(r)⊕m

Dec：对于输入的 k ∈ {0, 1}^n以及密文 c = <r, s>，输出明文 m := Fk(r)⊕s

THEOREM 3.29 方案3.28是CPA安全的

如果F是一个伪随机函数，则由方案3.28构造的对于明文长度为 n 的私钥加密方案是CPA安全的

THEOREM 3.29 的证明

记方案3.28为Π= (Gen, Enc, Dec)

我们再构建一个新方案。这个新方案除了用真随机函数代替3.28中的伪随机函数，其他均相同。我们记为

有一个PPT敌手A，设q(n)为敌手 A 在安全参数为n的CPA窃听实验中询问预言机的次数上限，q必须存在某个多项式的上界。

我们用A来构造伪随机函数F的一个区分器D。区分器D的输入是函数O的预言机，区分器的目标是判断该预言机对应的函数O是否为伪随机函数

Distinguisher D：

D被给定1^n和预言机O，其中O满足

运行A(1^n)，当敌手A用消息m∈{0, 1}^n询问预言机时，D随机均匀选择一个r∈{0, 1}^n并用r询问预言机，得到结果y=O(r)，将密文c= <r, y⊕m>计算并返回给A
当A输出消息m0，m1∈{0,1}^ n时，D随机均匀选择b∈{0, 1}，并且均匀选择一个r∈{0, 1}^n并用r询问预言机，得到结果y=O(r)，将密文c= <r, y⊕mb>计算并返回给A
A仍保持步骤1.中询问预言机的权利，直到A输出b’。D获取敌手A输出的b'，如果 b = b'，则D输出 1；否则D输出0

重点如下：

如果区分器D的预言机对应于伪随机函数，那么当A作为D的子程序运行时，以A的视角来看，A就相当于在做实验

因此，得到A式

如果区分器D的预言机对应于真随机函数，那么当A作为D的子程序运行时，以A的视角来看，A就相当于在做实验

因此，得到B式

由于F是一个伪随机函数，根据伪随机函数的定义，

现代密码学导论-17-伪随机函数_南鸢北折的博客-CSDN博客

DEFINITION 3.24 伪随机函数的正式定义

存在一个可以忽略的函数negl，满足C式

联立A、B、C式，得到D式

这个式子的形式非常像EAV-安全的第二个等价定义。但是对于CPA安全，我们还没有考虑过。

考虑实验

请注意，每次消息m被加密时，即询问预言机或当挑战密文被计算时，会随机均匀选择一个r∈{0, 1}^n，并计算c= <r, f(r)⊕m>。我们设r*表示在生成挑战密文<r*, f(r*)⊕m>时使用的随机字符串。有两种可能性：

如果r*在预言机对A的回答中没有出现过，由于f是真随机函数，A与预言机的交互中不能获得关于f(r*)的任何信息，那么A输出的b'=b的概率就是1/2
如果r*在预言机对A的回答中出现过，也就是说 A 获取了<r*, f(r*)⊕m>，那么其可以通过计算 f(r*)=f(r*)⊕m⊕m 就能得出f(r*)，在得知了 f(r*) 的情况下，A输出的b'=b的概率就为1

但是，A最多只能对预言机查询q(n)次，因此，A最多获得q(n)个r。由于r*是从{0, 1}^n中随机均匀选取的，因此有2^n种可能。那么A获取的r中包含r*的可能性就为q(n)/(2^n)

把事件“r* 被A捕获” 记为事件Repeat，则Pr[Repeat] ≤ q(n)/(2^n)

我们得到