⛄一、拓展卡尔曼滤波时序四旋翼无人机状态跟踪

卡尔曼滤波算法为获得最优估计和最小误差方差，将从目标模型中得到的测量值一步步递推，实时获取新时刻的状态估计值。

假设目标状态方程和观测方程分别为：

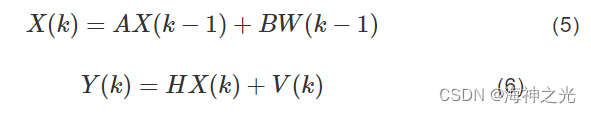
其中，k为离散时间，X(k)为系统在k时刻的状态，Y(k)为观测信号，W(k)为过程噪声，V(k)为观测噪声，A是状态转移矩阵，B是噪声驱动矩阵，H是观测矩阵。假设W(k)和V(k)是均值为零，方差各为Q和R的不相关白噪声。

目标在k时刻的估计值，即卡尔曼滤波算法的数学表达式[12]如下：

状态一步预测为：

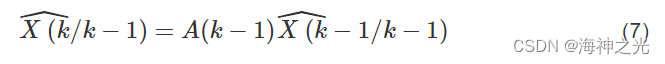
协方差一步预测为：

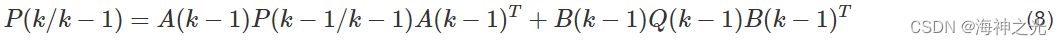
卡尔曼滤波增益为：

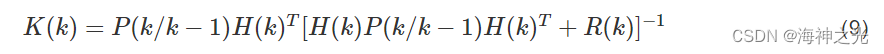
状态更新为：

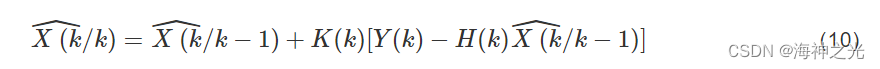
状态协方差更新为：

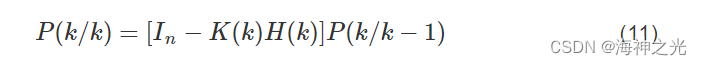
以上数学表达式表明，通过目标上一时刻的状态估计值预测出当前时刻的状态估计值，再得到当前时刻的更新值。卡尔曼滤波算法流程图如图1所示：

图1 卡尔曼滤波算法流程图
卡尔曼滤波算法在目标的轨迹跟踪中具有很好的性能，而且还有很强的适应能力，能够对状态值等进行实时处理，这些优势在后续的仿真中得以应用。

⛄二、部分源代码

clear all;
close all
N=200;
bsx(1)=1;
p(1)=10;
Z=randn(1,N)+25;
R = std(Z).^2;
w=randn(1,N);
Q = std(w).^2;
for t=2:N;
x(t)=bsx(t-1);

p1(t)=p(t-1)+Q;

kg(t)=p1(t)/(p1(t)+R);

bsx(t)=x(t)+kg(t)*(Z(t)-x(t));

p(t)=(1-kg(t))*p1(t);

end
t=1:N;
plot(t,bsx,‘r’, t,Z,‘g’, t,x,‘b’); % 红色线最优化估算结果滤波后的值，%绿色线观测值，蓝色线预测值
legend(‘Kalman滤波结果’,‘观测值’,‘预测值’);

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]许奕,邢传玺,万志良,姜佳圆.基于卡尔曼滤波算法的多AUV定位技术研究[J].云南民族大学学报(自然科学版).

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除