1. 不可观的解释

这篇论文中对VIO的4-DOF不可观的定义如下，可以看到这种不可观就是如果对最后求得的解进行一个四自由度的变换（类似单应变换），那么损失函数 $J(\theta)$ 并不会改变，所以这就是4-DOF的不可观。

另外从公式这个角度出发也是理解不可观的自由度的一种方式，例如VIO的yaw轴不可观，实际上就是把最后估计的位姿的yaw角再加上一个角度，不会改变损失函数。而这个加上yaw角，利用公式来理解就是把最后的位姿 绕着垂直于重力的 $z$ 再进行旋转。

在这里插入图片描述

2. 几种不同的gauge handle处理方式

仿真模型如下，第0次滑窗优化的时候状态变量是 $P_0, P_1, P_2, L$ 。显然这个系统是1自由度不可观的，所以下面要通过不同的方式来处理这个不可观的自由度。

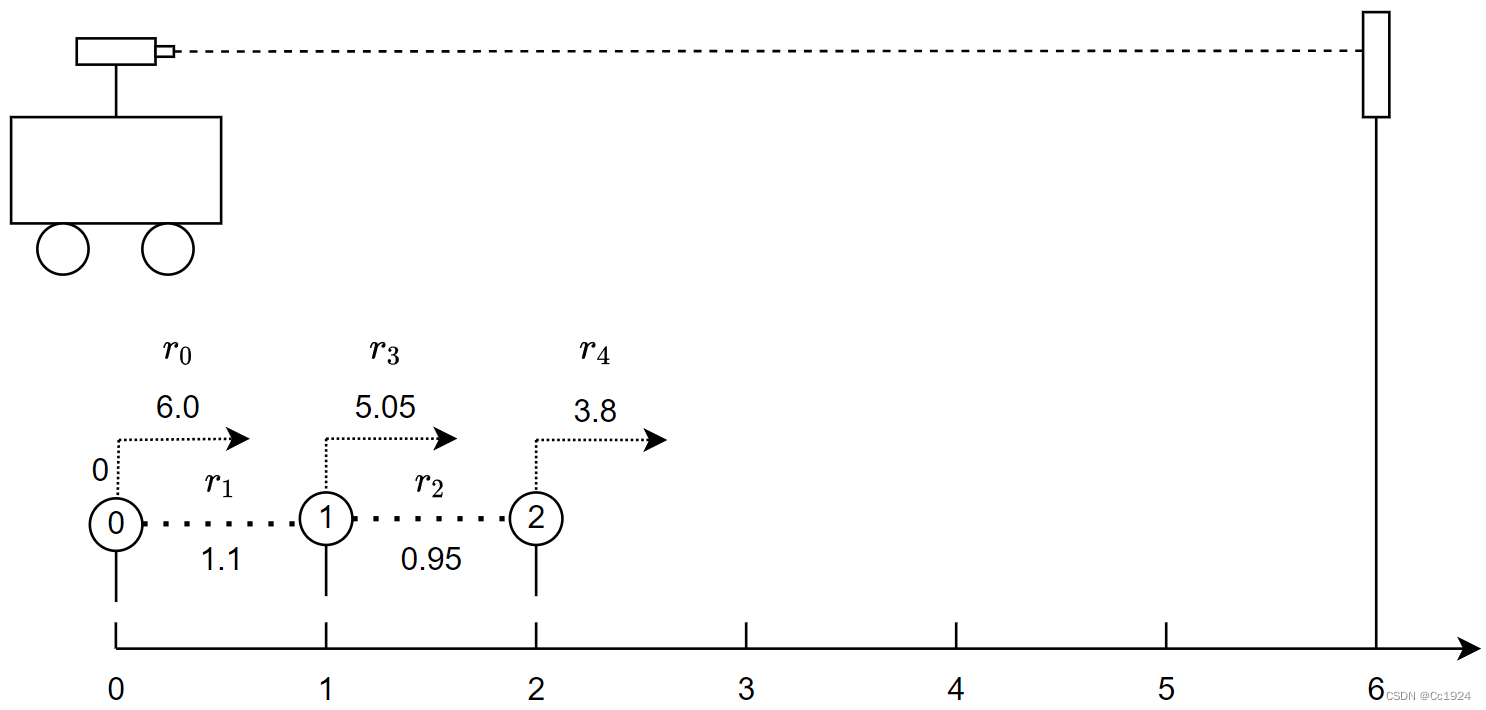
在这里插入图片描述
先给出此时系统的残差、雅克比矩阵以及H矩阵：
$\begin{aligned} r &= \begin{bmatrix} 6.0 - (L - P_0) \\ 1.1 - (P_1 - P_0) \\ 0.95 - (P_2 - P_1) \\ 5.05 - (L - P_1) \\ 3.8 - (L - P_2) \end{bmatrix} \\\\ J &= \begin{bmatrix} 1 & 0 & 0 & -1 \\ 1 & -1 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \end{bmatrix} \\\\ H = J'J &= \begin{bmatrix} 2 & -1 & 0 & -1 \\ -1 & 3 & -1 & -1 \\ 0 & -1 & 2 & -1 \\ -1 & -1 & -1 & 3 \end{bmatrix} \end{aligned}$
容易发现， $H$ 矩阵的每一行都加起来结果为0，所以 $H$ 矩阵是不满秩的， $r ank (H) = 3$ ，所以需要进行一些特殊的处理才能求解。

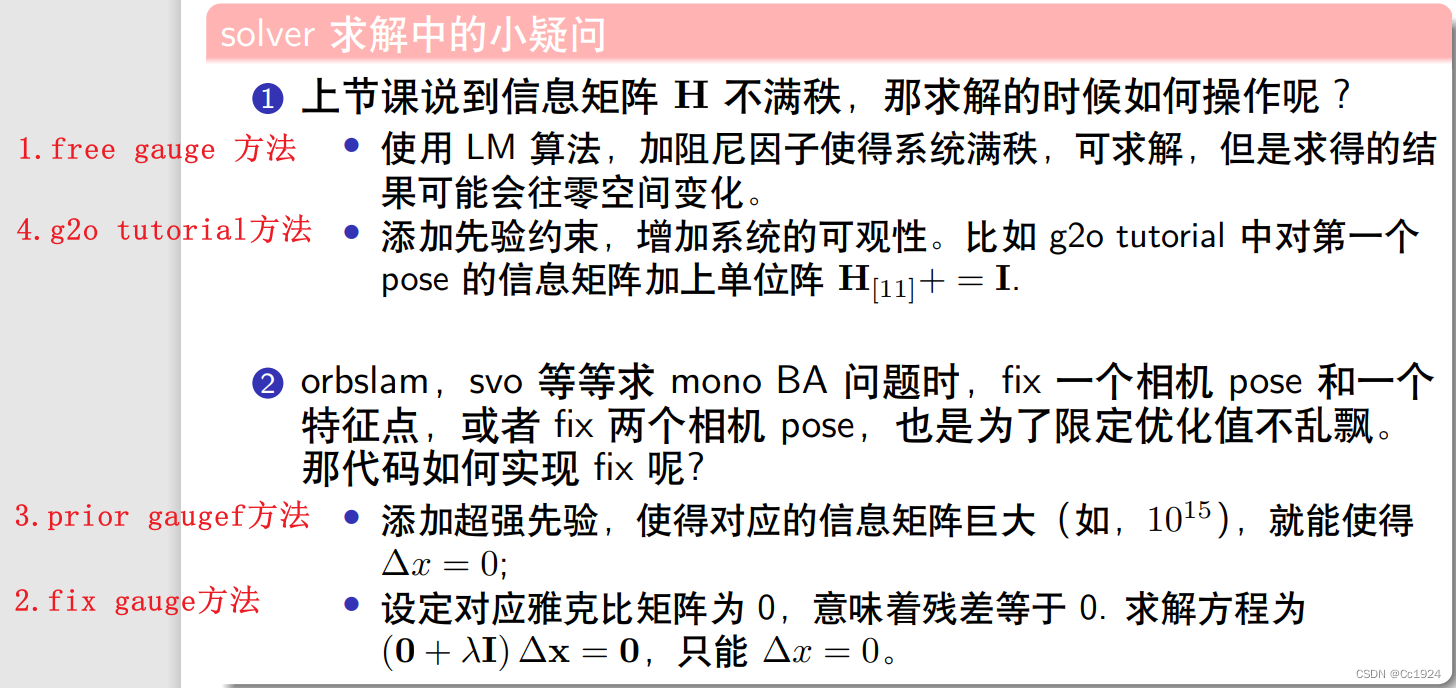
这种存在自由度不可观的情况在论文中称为 gauge freedom，处理 gauge freedom（称为gauge handle）有多种方式，这篇论文总结为下面三种方式（g2o中还有一种方式，这里定义为第4种）。实际上在VIO的课程中，总结的应该是四种，恰好对应下面自己写的这四种。

在这里插入图片描述

2.1. free gauge方式

不管这个自由度，而 $H\Delta x=-b$ 的求解 $H$ 不满秩的问题靠 L-M算法中给 $H$ 增加一个 $\lambda I$ 来间接解决（因为本来 $\lambda I$ 是为了限制高斯牛顿法接近二次拟合的）。但是这样的结果最后 仍然会在零空间漂移，所以在VINS中用的做法就是使用free gauge求解 $\Delta x$ ，但是求解之后给变量赋值的时候，是让第滑窗中第0帧的4-DOF保持不变，也就是认为第0帧的状态不发生改变。

MATLAB 代码如下：

%% 本代码测试不同的零空间处理方法gauge handle
clear all; clc;

%% 0.正常状态，滑窗中维护3个位置+1个路标点
% 真实状态
x_t = [0; 1; 2; 6];  % 滑窗长度为3, 变量分别为P0, P1, P2, L
% 码盘测量值, e=encoder, l=lidar
l0 = 6.0; e1 = 1.1; e2 = 0.95; l1 = 5.05; l2 = 3.8;
e0 = 0.0;  % 为了解决漂移的问题，给一个超强先验
% 状态初值, 由码盘测量值来得到
P0 = e0; P1 = P0 + e1; P2 = P1 + e2; L = P0 + l0; 
% 状态初始估计值
x = [P0; P1; P2; L]; 

%% gauge handle 1: free gauge
disp("****** gauge handle 1: free gauge ******");
J = [1, 0, 0, -1;
     1, -1, 0, 0; 
     0, 1, -1, 0;
     0, 1, 0, -1;
     0, 0, 1, -1];
H = J' * J
fprintf("rank(H) = %d\n", rank(H));  % rank(H) = 3
miu = 0.1;
H = H + miu * eye(4);
% 其实由于是线性模型，所以没必要迭代，一步就是最速下降法得到最优解
for i = 1 : 5   
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r = [l0 - (x(4) - x(1));
         e1 - (x(2) - x(1)); 
         e2 - (x(3) - x(2));
         l1 - (x(4) - x(2));
         l2 - (x(4) - x(3))];
    b = -J' * r;
    delta_x = H \ b;
    x = x + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x = "); disp(x');
end
x = x + 0 - x(1);  % 手动对齐第0帧的位置到想要的位置上
disp("x = "); disp(x');
fprintf("error = %f\n", (x_t-x)' * (x_t-x));

代码输出如下：
在这里插入图片描述

2.2. fix gauge方式

固定滑窗中的第0帧，具体操作就是和滑窗中的 第0帧有关的雅克比矩阵全都置为0，这就意味第0帧的变化对所有的残差都不会有贡献，所以第0帧在优化中就不会改变了。

从数学上来看，也就是上面仿真的例子中雅克比矩阵 $J$ 的第1列（对应状态 $P_0$ ）全为0，即：

$\begin{aligned} J &= \begin{bmatrix} 0 & 0 & 0 & -1 \\ 0 & -1 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \end{bmatrix} \\\\ H = J'J &= \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 3 & -1 & -1 \\ 0 & -1 & 2 & -1 \\ 0 & -1 & -1 & 3 \end{bmatrix} \\\\ b = -J'e &= \begin{bmatrix} 0 \\ ... \\ ... \\ ... \end{bmatrix} \end{aligned}$

由于最后我们求解还是使用 L-M算法求解，即会在 $H$ 矩阵对角线上加一个数 $\mu$ ，所以最后求解的方程变成

$\begin{bmatrix} \mu & 0 & 0 & 0 \\ 0 & 3+\mu & -1 & -1 \\ 0 & -1 & 2+\mu & -1 \\ 0 & -1 & -1 & 3+\mu \end{bmatrix} \begin{bmatrix} \Delta P_0 \\ \Delta P_1 \\ \Delta P_2 \\ \Delta L \\ \end{bmatrix} = \begin{bmatrix} 0 \\ ... \\ ... \\ ... \end{bmatrix}$

这时候关于 $\Delta P_0$ 这一项的解就变成了 $(0+\mu)\Delta P_0 = 0$ ，结果只能是 $\Delta P_0 = 0$ ，从而起到了固定第0帧的位置的作用。我感觉这个本质上属于 一种数学技巧，并不是很有物理意义。

代码实现如下：

%% gauge handle 2: fix gauge
fprintf("\n");
disp("****** gauge handle 2: fix gauge ******"); 
x = [P0; P1; P2; L]; 
% 雅克比第1列是关于状态P0的，全部置为0
J = [0, 0, 0, -1;
     0, -1, 0, 0; 
     0, 1, -1, 0;
     0, 1, 0, -1;
     0, 0, 1, -1];
H = J' * J
fprintf("rank(H) = %d\n", rank(H));  % rank(H) = 3
miu = 0.1;
H = H + miu * eye(4);

for i = 1 : 5 
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r = [l0 - (x(4) - x(1));
         e1 - (x(2) - x(1)); 
         e2 - (x(3) - x(2));
         l1 - (x(4) - x(2));
         l2 - (x(4) - x(3))];
    b = -J' * r;
    delta_x = H \ b;
    x = x + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x = "); disp(x');
end
fprintf("error = %f\n", (x_t-x)' * (x_t-x));

代码输出如下，可见迭代速度不快，这个迭代速度可以通过调节 $\mu$ 来改变。

2.3. prior gauge方式

给滑窗中的第0帧添加先验，这种方式实际上是 最正规的方式，因为它有明确的物理意义，而其他方式更像是一种数学上的技巧。这种添加先验的方式就是从存在不可观的原因出发，即由于测量全都是相对测量而没有绝对测量，导致优化结果可以漂移。所以这种方式就是增加一个绝对位置的先验测量，比如给滑窗中第0帧添加一个先验观测的位置是0，这样优化的时候最终结果就不会离0太远。

（1） 如果想固定第0帧就是在先验观测0的位置，那么只需要把这个先验观测的协方差矩阵设置的非常小，也就是信息矩阵（权重）设置的非常大，这样优化状态离先验观测稍微偏离一点就会造成非常大的误差项，从而最后会把第0帧的优化状态固定在先验的位置。

（2） 如果就是有一个实际观测到的先验，比如GPS观测，有明确的协方差矩阵，那么就可以把它作为先验融合到滑窗优化中，这样滑窗中第0帧位置可能会发生变化，但是此时就是需要让它有变化，因为我们已经有先验了，需要来修正这个状态。

代码如下：

%% gauge handle 3: prior gauge
fprintf("\n");
disp("****** gauge handle 3: prior gauge ******"); 
x = [P0; P1; P2; L];
w = 30;   % 超强先验的权重，注意一定是正数。而且这个数值还不能太大，如果太大会导致H矩阵直接退化成rank=1
J = [-w, 0, 0, 0;   % 超强先验, 残差是 w(e0 - P0), 所以雅克比是-w
     1, 0, 0, -1;
     1, -1, 0, 0; 
     0, 1, -1, 0;
     0, 1, 0, -1;
     0, 0, 1, -1];
% 开始构造高斯牛顿的优化问题，认为信息权重矩阵都是I
H = J' * J
fprintf("rank(H) = %d\n", rank(H));  % rank(H) = 4

% 其实由于是线性模型，所以没必要迭代，一步就是最速下降法得到最优解
for i = 1 : 2   
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r = [ w * (e0 - x(1));
         l0 - (x(4) - x(1));
         e1 - (x(2) - x(1)); 
         e2 - (x(3) - x(2));
         l1 - (x(4) - x(2));
         l2 - (x(4) - x(3))];
    b = -J' * r;
    delta_x = H \ b;
    x = x + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x = "); disp(x');
end
fprintf("error = %f\n", (x_t-x)' * (x_t-x));

代码输出：

注意：

如果是想固定第0帧的话，给的先验权重大小要合适。首先不能太小，否则起不到固定的效果；其次也不能太大，否则此时的 $H$ 矩阵中数值差异过大，会直接导致 $H$ 矩阵的秩变成1，相当于整个 $H$ 矩阵中只有 $ww$ 构成的这一项，因为其他项相比它都太小了，这样反而会直接导致系统更加不可观。
可以发现这种方式系统一次就迭代到了最小值，到底这几种方法为什么会有这种迭代速度的区别还需要后面仔细思考。但是根据论文里说的，这几种方法实际上速度差别不大。

2.4. g2o tutorial方式

这种方式也是属于 固定第0帧，具体叫什么名字不知道，在手写VIO的课程中有讲解，因为g2o就是使用的这种方式来固定某些帧，所以这里就称之为g2o tutorial的方式了。

其操作就是在最后的 $H$ 矩阵要固定的状态变量的位置强行加一个 $I$ ，但是对应的 $b$ 的位置并不加任何东西。这样其实本质上就是更改了原来的 $H\Delta x = b$ 的方程组，导致求解的结果中 $\Delta x_0$ 只能为0。所以这个本质上也属于一种 数学技巧，并没有物理意义。

比如上面的例子，假设 $H\Delta x = b$ 的形式如下：

$\begin{bmatrix} h_{11} & h_{12} & h_{13} & h_{14} \\ h_{21} & h_{22} & h_{23} & h_{24} \\ h_{31} & h_{32} & h_{33} & h_{34} \\ h_{41} & h_{42} & h_{43} & h_{44} \end{bmatrix} \begin{bmatrix} \Delta P_0 \\ \Delta P_1 \\ \Delta P_2 \\ \Delta L \\ \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \end{bmatrix} \\$
现在想要固定 $P_0$ 的位置，那么就给 $H$ 矩阵对应 $P_0$ 的位置增加一个单位阵 $I$ ，这样上面的方程变为：

$\begin{bmatrix} h_{11} + 1 & h_{12} & h_{13} & h_{14} \\ h_{21} & h_{22} & h_{23} & h_{24} \\ h_{31} & h_{32} & h_{33} & h_{34} \\ h_{41} & h_{42} & h_{43} & h_{44} \end{bmatrix} \begin{bmatrix} \Delta P_0 \\ \Delta P_1 \\ \Delta P_2 \\ \Delta L \\ \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \end{bmatrix} \\$

利用矩阵的乘法分配律，可以把上述方程拆解为两个方程：

$\begin{aligned} \begin{bmatrix} h_{11} & h_{12} & h_{13} & h_{14} \\ h_{21} & h_{22} & h_{23} & h_{24} \\ h_{31} & h_{32} & h_{33} & h_{34} \\ h_{41} & h_{42} & h_{43} & h_{44} \end{bmatrix} \begin{bmatrix} \Delta P_0 \\ \Delta P_1 \\ \Delta P_2 \\ \Delta L \\ \end{bmatrix} &= \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \end{bmatrix} \\\\ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} \Delta P_0 \\ \Delta P_1 \\ \Delta P_2 \\ \Delta L \\ \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \end{aligned}$

可见我们可以利用第2个方程先求写出 $\Delta P_0 = 0$ ，然后带入到第1个方程中再求解处剩下的变量。也就是说，实际上这种方式就是在原来的4个方程的基础上又增加了一个附加方程为 $\times \Delta P_0 = 0$ ，从而强行改变了原来方程组的解。所以这个本质上也属于一种 数学技巧，并没有物理意义。

代码如下：

%% gauge handle 4: g2o tutorial
fprintf("\n");
disp("****** gauge handle 4: g2o tutorial ******"); 
x = [P0; P1; P2; L]; 
J = [1, 0, 0, -1;
     1, -1, 0, 0;  
     0, 1, -1, 0;
     0, 1, 0, -1;
     0, 0, 1, -1];
H = J' * J
fprintf("rank(H) = %d\n", rank(H));  % rank(H) = 3
H(1, 1) = H(1, 1) + 1;

% 其实由于是线性模型，所以没必要迭代，一步就是最速下降法得到最优解
for i = 1 : 2   
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r = [l0 - (x(4) - x(1));
         e1 - (x(2) - x(1)); 
         e2 - (x(3) - x(2));
         l1 - (x(4) - x(2));
         l2 - (x(4) - x(3))];
    b = -J' * r;
    delta_x = H \ b;
    x = x + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x = "); disp(x');
end
fprintf("error = %f\n", (x_t-x)' * (x_t-x));