题目1(IIR):
已知一个系统的传递函数为:
H
(
z
)
=
8
−
4
z
−
1
+
11
z
−
2
−
2
z
−
3
1
−
1.25
z
−
1
+
0.75
z
−
2
−
0.125
z
−
3
H(z)=\frac{8-4z^{-1}+11z^{-2}-2z^{-3}}{1-1.25z^{-1}+0.75z^{-2}-0.125z^{-3}}
H(z)=1−1.25z−1+0.75z−2−0.125z−38−4z−1+11z−2−2z−3
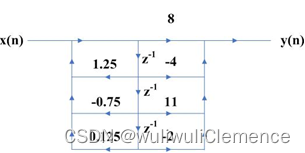
将其由直接型转换为级联型、并联型。信号流图如下图所示。
我们先来认识MATLAB自带的两个函数。
residuez
residuez 函数用于计算有理多项式函数在复平面内的极点和残差。其输入参数为分子多项式的系数向量 b 和分母多项式的系数向量 a,输出参数包括极点向量 p、残差向量 r 和常数项 k。
tf2sos
tf2sos 函数则将有理分式函数的分子和分母多项式转换为一组二阶段的、单精度二进制浮点数实现的二阶IIR滤波器系数。tf2sos 的输入参数是分子多项式的系数向量 b 和分母多项式的系数向量 a,输出参数是用于实现滤波器的二阶段滤波器系数 sos 和全局增益 g。
在实际应用中,tf2sos 函数通常用于将高阶滤波器分解为多个二阶IIR滤波器级联的形式,以便更容易实现和分析。而 residuez 函数则常用于计算一些特殊类型的系统的响应,如倒数函数、正切函数等。
代码
b=[8,-4,11,-2];
a=[1,-1.25,0.75,-0.125];
[r,p,c]=residuez(b,a)
[sos,g]=tf2sos(b,a)
部分分式,并联型

H
(
z
)
=
−
8
−
12
i
1
−
(
0.5
+
0.5
i
)
z
−
1
+
−
8
+
12
i
1
−
(
0.5
−
0.5
i
)
z
−
1
+
8
1
−
0.25
z
−
1
+
16
H(z)=\frac{-8-12i}{1-(0.5+0.5i)z^{-1}}+\frac{-8+12i}{1-(0.5-0.5i)z^{-1}}+\frac{8}{1-0.25z^{-1}}+16
H(z)=1−(0.5+0.5i)z−1−8−12i+1−(0.5−0.5i)z−1−8+12i+1−0.25z−18+16
相乘,级联型

H
(
z
)
=
8
∗
1
−
0.19
z
−
1
1
−
0.25
z
−
1
∗
1
−
0.31
z
−
1
+
1.3161
z
−
2
1
−
z
−
1
+
0.5
z
−
2
H(z)=8*\frac{1-0.19z^{-1}}{1-0.25z^{-1}}*\frac{1-0.31z^{-1}+1.3161z^{-2}}{1-z^{-1}+0.5z^{-2}}
H(z)=8∗1−0.25z−11−0.19z−1∗1−z−1+0.5z−21−0.31z−1+1.3161z−2
题目2(FIR):
横截型与级联型之间的转换
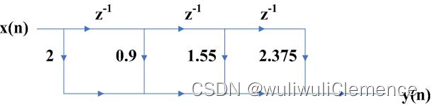
已知一个FIR系统的传递函数为
H
(
z
)
=
2
+
0.9
z
−
1
+
1.55
z
−
2
+
2.375
z
−
3
H(z)=2+0.9z^{-1}+1.55z^{-2}+2.375z^{-3}
H(z)=2+0.9z−1+1.55z−2+2.375z−3
将其从横截型转换为级联型。信号流图如下所示。
程序
b=[2,0.9,1.55,2.375];
a=[1];
[sos,g]=tf2sos(b,a)
运行结果:

H
(
z
)
=
2
(
1
+
0.95
z
−
1
)
(
1
−
0.5
z
−
1
+
1.25
z
−
1
)
H(z)=2(1+0.95z^{-1})(1-0.5z^{-1}+1.25z^{-1})
H(z)=2(1+0.95z−1)(1−0.5z−1+1.25z−1)