最近开算法课,开几篇文章记录一下算法的学习过程。
关于算法的重要性
学习计算机当程序员的话,在编程过程中是绕不开算法这个大矿山的,需要我们慢慢挖掘宝藏。
算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但在过程中消耗的资源和时间却会有很大的区别。
时间复杂度
先了解一下关于时间复杂度的相关概念:
涉及到代码所用时间,我们可以琢磨把代码跑一遍记录一下起始和结束的时间得出整个算法用时,但是很多情况我们是需要理论分析的,不是上机测试,另外硬件的不同也会导致时间有差异。这时候就出现了一个叫做大O表示法。
算法的时间复杂度,用来度量算法的运行时间,记作: T(n) = O(f(n))。它表示随着 输入大小n 的增大,算法执行需要的时间的增长速度可以用 f(n) 来描述。
时间复杂度分析的基本策略是:从内向外分析,从最深层开始分析。如果遇到函数调用,要深入函数进行分析
常见描述时间复杂度的表达式:
O(1):常量时间
O(n):线性时间
O(log n):对数时间
O(n^2):二次方时间
O(2^n):指数时间
O(n!):阶乘时间
常见的算法时间复杂度分析:
O(1)< O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) <O(n!) < O(n^n)
如何计算时间复杂度
O(1)
int func(int n)
{
n++;
return n*2;
}
上面代码运行时间是一个常量,虽然运行时间是2,但是用O(1)表示,代表时间复杂度是一个常数。
O(n)
int func(int n)
{
int sum = 0;
for(int i=0; i<n; i++)
{
sum = sum + i;
}
return sum;
}
上面程序我们分析函数的执行时间是随着n的变化成线性关系:n+2,用O(n)表示线性。
O(n^2 )
int func(int n)
{
int sum = 0;
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
{
sum = sum + i + j;
}
}
return sum;
}
上面的程序是两层循环的程序,函数的执行时间是n的2次方关系:n^2+2 ,用O(n^2 )来表示时间复杂度。(关于为什么可以省去低幂的我们下面会说明)
O(2^n)
O(2^n)表示指数复杂度,随着n的增加,算法的执行时间成倍增加,它是一种爆炸式增长的情况。
int func(int n)
{
if(n==0) return 1;
return func(n) + func(n-1)
}
O(log n)
O(log n)表示对数时间复杂度,算法执行时间和n是一种对数关系。这种类型的算法会在执行的过程中,随着程序的执行其完成某个功能的操作步骤越来越少。 其中,我们所熟知的二分查找法就是一个很好的例子。比如,下面这个代码在一个有序列表中查找某个值的位置,我们通过二分法进行查找。
int func(int a[], int size, int num)
{
int left = 0;
int right = size-1;
while(left <= right)
{
int mid = (left + right)/2;
if(a[mid] > num)
{
right = mid - 1;
}
else if (a[mid] < num)
{
left = mid + 1;
}
else
{
return num;
}
}
return -1;
}
O(n!)
这个我不是很了解,找一个网上的例子来说说吧。
旅行商问题
假设有一个旅行商人要拜访n+1个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径长度为所有路径之中的最小值。
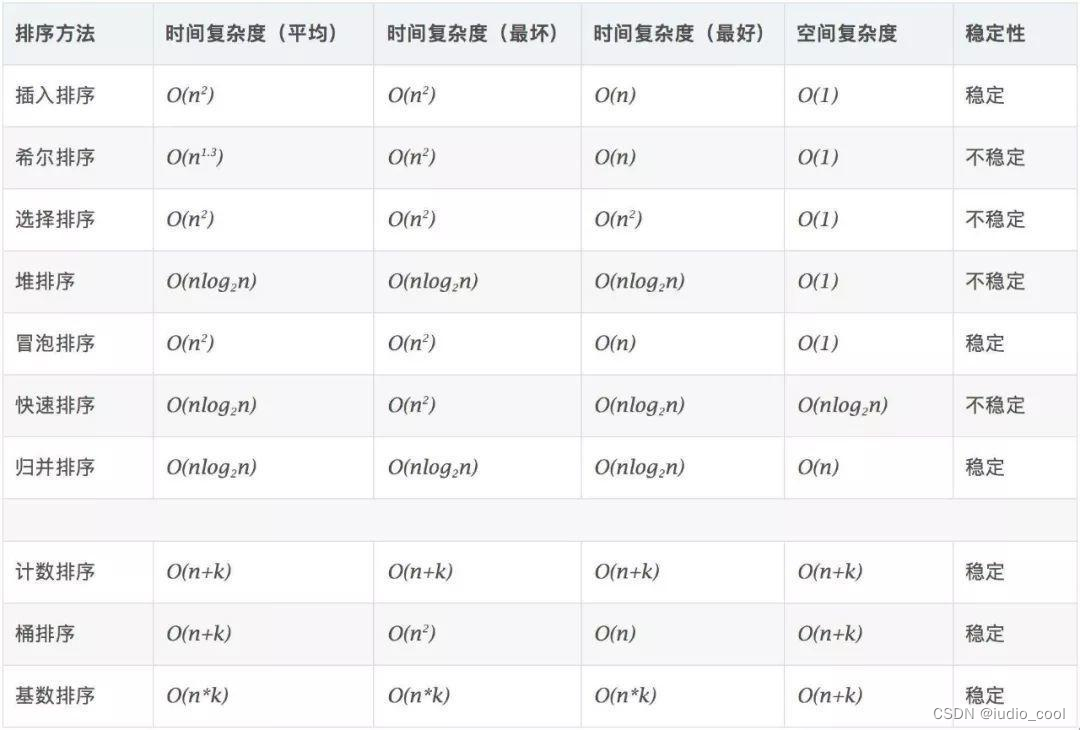
常见算法的时间复杂度