乘法硬件原理

结论

可以将乘法A x B转为A的移位相加。
利用$乘2^n就是左移n位的特性$，将数拆分为$2^n$表示

思路1

原始列竖式计算方法ref例2.9

思路2

B总是可以拆分为：$B=(a_n{2}^n+a_{n-1}{2}^{n-1}+...+a_1{2}^1+a_0{2}^0)$
　　例如：B=4’d10=$1\ast 2^3+0\ast 2^2+1\ast 2^1+0\ast 2^0$=4’b1010

举例

$3\ast 10=3\ast (4^{\prime }b1010)=3\ast (2^3+2^1)=3<<3+3<<1=24+6=30$

编码

思路1采用原始手算,列竖式思路

思路2采用移位思路：

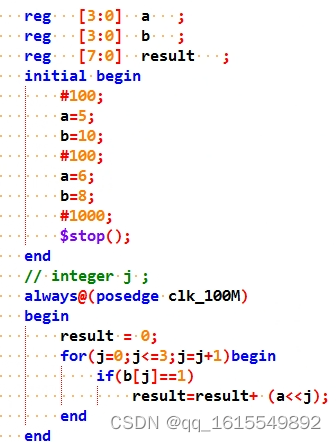
仿真

综合

思路1综合如下：

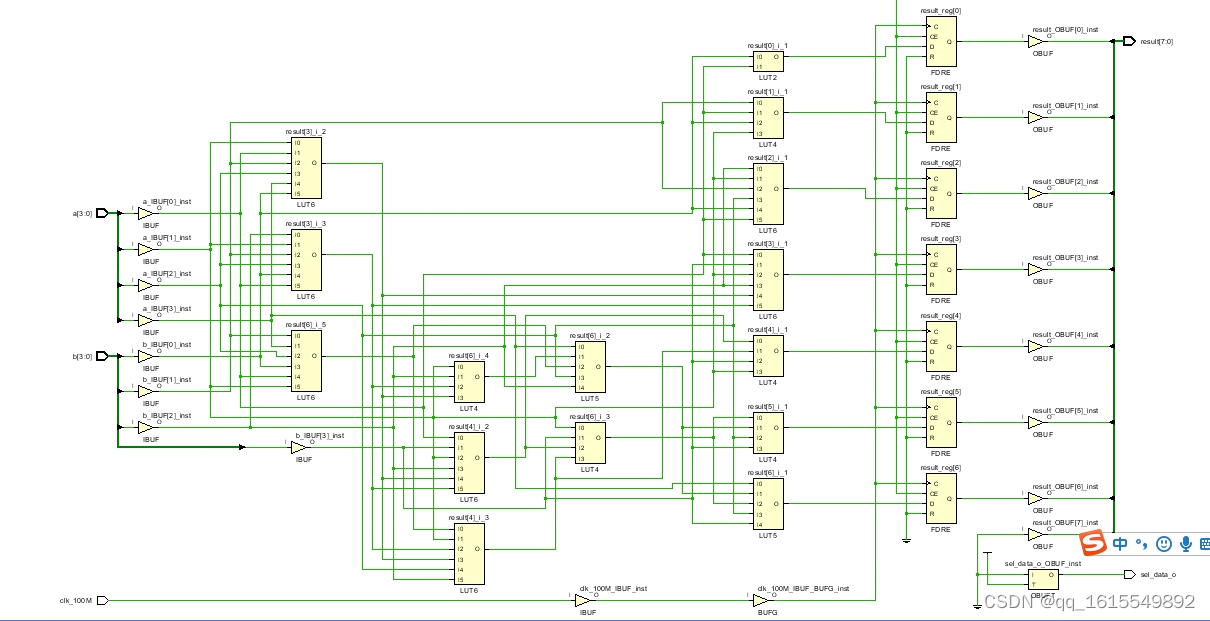
思路2综合如下：

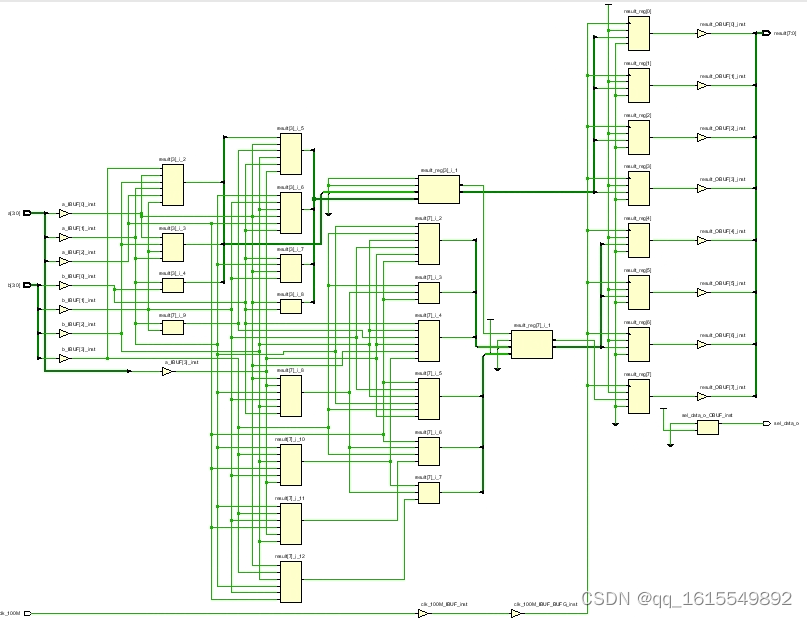
思路1原始竖式方法的资源：

思路2移位方法的资源：

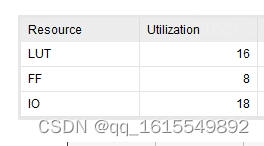
搞半天，原始的方法占资源还少，离谱。

除法硬件原理

我是参考这这个博主的这篇，他写的很好可以先看。
就是手算的思路，改成了硬件方便的实现。移位相减。

verilog代码

仿真结果

资源占用

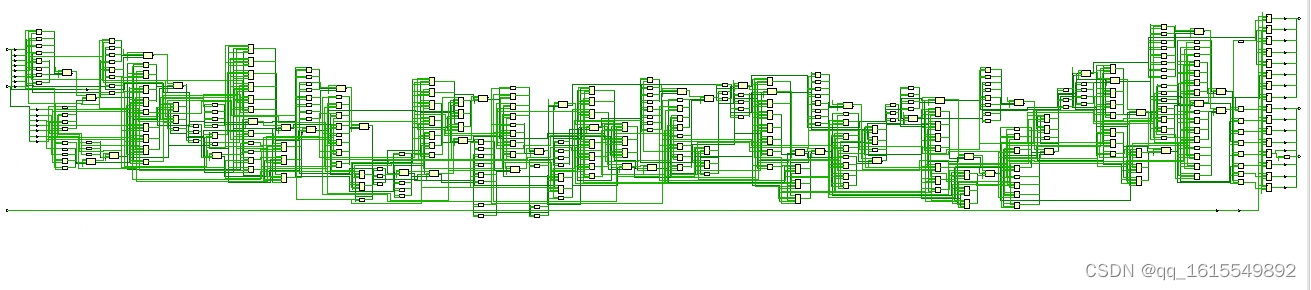
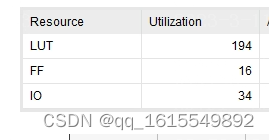
可以看到资源占不少啊！并且时序也不好。