人工智能实验一：利用遗传算法求解 TSP（旅行商）问题

news2024/11/27 1:35:45

1.任务描述

本关任务：利用遗传算法求解 TSP 问题。

2.相关知识

为了完成本关任务，你需要掌握：1. 遗传算法；2. TSP问题。

遗传算法

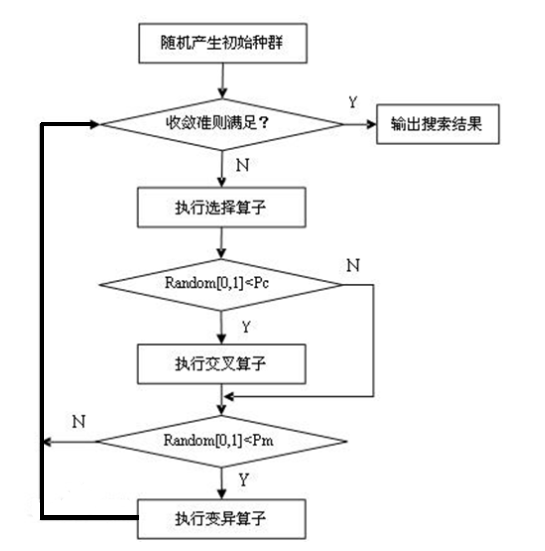
一个后继状态由两个父状态决定，以k个随机产生的状态开始（population），一个状态表示成一个字符串。

定义一个健康度量函数用来评价状态的好坏程度，通过选择，交叉，突变的操作产生下一轮状态。

img

TSP问题

旅行商问题，即 TSP 问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。

假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。

3.编程要求

在右侧编辑器中补充void select()和void cross()函数，解决 TSP 问题，求所有路径中的最小路径路程。

4.测试说明

平台会对你编写的代码进行测试：

预期输出：18

5.实验过程

下面是关于非补充部分的代码解释：

1.宏定义一些常量，用来简化代码，提高效率

#define cityNum 10          //城市数量				
#define popSize 10          //种群大小
#define croRate 0.85		//交叉概率   
#define mutRate 0.1			//变异概率
#define MAX 999				//最大距离

2.定义“染色体”结构体，一个染色体用于标识一个个体

struct Chrom
{
    int cityArr[cityNum];   //城市编号
    char name;              //染色体名称
    float adapt;            //个体适应度
    int dis;                //个体距离
};

3.定义种群和新种群以及临时变量

struct Chrom genes[popSize];        //种群
struct Chrom genesNew[popSize];     //新种群
struct Chrom temp;

4.定义十个城市名以及其之间的距离，用邻接矩阵表示

char names[cityNum] = { 'A','B','C','D','E','F','G','H','I','J' };      //城市名

int distance[cityNum][cityNum] = { { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9  },
    {  1, 0, 1, 2, 3, 4, 5, 6, 7, 8  },
    {  2, 1, 0, 1, 2, 3, 4, 5, 6, 7  },
    {  3, 2, 1, 0, 1, 2, 3, 4, 5, 6  },
    {  4, 3, 2, 1, 0, 1, 2, 3, 4, 5  },
    {  5, 4, 3, 2, 1, 0, 1, 2, 3, 4  },
    {  6, 5, 4, 3, 2, 1, 0, 1, 2, 3  },
    {  7, 6, 5, 4, 3, 2, 1, 0, 1, 2  },
    {  8, 7, 6, 5, 4, 3, 2, 1, 0, 1  },
    {  9, 8, 7, 6, 5, 4, 3, 2, 1, 0  }
};     //距离邻接矩阵

5.void initGroup()函数：用于初始化群体，生成一组随机的染色体

void initGroup()
{
    int i, j, k;
    int t = 0;
    int flag = 0;
    srand(time(NULL));                  //用于初始化随机数种子，time(NULL)返回当前系统时间
    for (i = 0; i < popSize; i++)       //每次生成一个染色体
    {

        temp.name = names[i];           //定义temp结构体，记录染色体的名称、适应度和距离
        temp.adapt = 0.0f;
        temp.dis = 0;

        for (j = 0; j < cityNum;)
        {
            t = rand() % cityNum;       //每次在城市列表中随机选取一个城市编号
            flag = 1;
            for (k = 0; k < j; k++)
            {
                if (genes[i].cityArr[k] == t)   //判断选取的城市是否已经被选中
                {
                    flag = 0;
                    break;
                }
            }
            if (flag)                   //选取的城市没有被选中
            {
                temp.cityArr[j] = t;    //存入数组中
                genes[i] = temp;        //生成一个完整的染色体
                j++;                    //j自增1
            }
        }
    }
}

6.void popFitness()函数：用于计算种群中每个个体的适应度值

void popFitness()       //计算种群中每个个体的适应度值
{
    int i, n1, n2;
    for (i = 0; i < popSize; i++)       //循环遍历种群中的所有个体
    {
        genes[i].dis = 0;               //初始化当前个体的路径长度为0
        for (int j = 1; j < cityNum; j++)       //循环遍历当前个体中所有的城市
        {
            n1 = genes[i].cityArr[j - 1];       //获取前一个城市的编号
            n2 = genes[i].cityArr[j];           //获取当前城市的编号
            genes[i].dis += distance[n1][n2];   //将前一个城市到当前城市的距离累加到路径长度中
        }
        //将最后一个城市到第一个城市的距离加到路径长度中，得到该个体的总路径长度
        genes[i].dis += distance[genes[i].cityArr[0]][genes[i].cityArr[cityNum - 1]];
        //计算当前个体的适应度值，并保存到genes数组中
        genes[i].adapt = (float)1 / genes[i].dis;
    }
}

7.int chooseBest()函数：从种群中选择适应度最高的个体

int chooseBest()
{
    int choose = 0;         //适应度最高的个体的索引
    float best = 0.0f;      //当前适应度最高的值
    best = genes[0].adapt;  //初始化当前适应度最高的值
    for (int i = 0; i < popSize; i++)
    {
        if (genes[i].adapt < best)      //如果当前个体的适应度值比当前适应度最高的值还小
        {
            best = genes[i].adapt;      //更新当前适应度最高的值
            choose = i;                 //更新适应度最高的个体的索引
        }
    }
    return choose;          //返回适应度最高的个体的索引
}

下面需要对代码进行补充

1.补充select()函数

选择操作是遗传算法中的一个重要步骤，它的作用是从当前种群中选出一些适应度较高的个体，作为下一代个体的双亲，从而保留优良的基因

常用的实现方法有: 适应度比例法，随机遍历抽样法，局部选择法，锦标赛选择法和 序选择法（轮盘赌方法）

这里我们使用轮盘赌方法：

  • 计算每个个体的适应度值和总适应度值
  • 计算每个个体被选中的概率
  • 生成一个0到1之间的随机数
  • 从第一个个体开始累加选择概率，直到大于或等于随机数为止
  • 返回当前累加到的个体作为选中结果

下面是具体代码实现：

void select()
{
    float biggestSum = 0.0f;            //定义适应度总和
    float adapt_pro[popSize];
    float pick = 0.0f;
    int i;
    for (i = 0; i < popSize; i++)       //计算适应度总和
    {
        biggestSum += genes[i].adapt;
    }
    for (i = 0; i < popSize; i++)       //计算每个个体的适应度占总适应度的比例
    {
        adapt_pro[i] = genes[i].adapt / biggestSum;
    }

    for (i = 0; i < popSize; i++)
    {
        pick = (float)rand() / RAND_MAX;    //随机选择一个个体
        /********** Begin **********/
        float sum = 0.0f;
        for (int j = 0; j < popSize; j++)
        {
            sum += adapt_pro[j];       //累加适应度比例
            if (sum > pick)            //当累加值超过pick时，选择对应的个体
            {
                genesNew[i] = genes[j];
                break;
            }
        }
        /********** End **********/
    }
    for (i = 0; i < popSize; i++)       //将新生成的种群genesNew复制到原来的genes数组中，以更新种群
    {
        genes[i] = genesNew[i];
    }
}

首先求出适应度总和，然后计算每个个体的适应度占总适应度的比例。遍历所有种群，每次遍历中随机生成一个0到1之间的随机数，用于模拟轮盘赌法中的轮盘转动，决定选择哪个个体。当某个个体的累加适应度比例超过这个随机数即可选择这个个体，因为它被选择的概率更高，适应度更高，基因更优良。接着将新种群复制回原种群数组中。

2.补充cross()函数

交叉操作是遗传算法中产生新个体的主要操作过程，它模拟了自然选择和遗传中发生的复制、交叉和变异等现象，以某一概率相互交换某两个个体之间的部分染色体

corss（)函数的主要思想是，从第一个第二个个体开始两两进行交叉，首先随机生成一个0-1之间的浮点数，如果大于交叉概率（已经宏定义），则不进行交叉操作。

其中move变量是用来控制交叉操作的次数和对象的，它表示当前要进行交叉操作的两个个体在种群中的位置。例如，如果move=0，那么就表示第一个个体和第二个个体要进行交叉操作。move变量每次增加2，直到达到种群大小popSize-1为止这样可以保证每两个相邻的个体都有一次机会进行交叉操作，并且不会重复或遗漏。

随机生成两个交叉点。这里使用这篇文章的例子

两个父代分别为：

  • 12|3456|789
  • 46|2738|159

其交叉点位置pos1和pos2分别为2和6。接着交换两个交叉点之间的基因片段，生成的两个子代分别为：

  • 12|2738|789
  • 46|3456|159

很明显两个子代都有基因冲突，比如第一个子代中2,7,8基因都有两个，会产生冲突，所以要补充函数用来解决冲突。一个办法是交换两个冲突子代中的冲突基因。

首先记录下冲突基因的位置，保存到conflict数组中。注意只看非交叉片段和交叉片段的冲突。如12|2738|789中12和2738中的2冲突，记录下12中2的下标位置。同理789和2738中的7和8冲突，记录789中7和8的下标位置。

因此conflict1[3]={1,6,7}，conflict2[3]={0,1,7}

接着将两个冲突子代的1和0,6和1,7和7的下标的对应基因进行交换，即可解决冲突，新生成的子代为：

  • 14|2738|659
  • 27|3456|189

代码如下：

void cross()
{
    float pick;
    int choice1, choice2;       //交叉的两个父代
    int pos1, pos2;             //记录交叉点位置
    int temp;
    int conflict1[popSize];     //记录父代1的冲突基因位置
    int conflict2[popSize];     //记录父代2的冲突基因位置
    int num1;                   //num用来记录冲突基因个数，且两个父代冲突基因数相同
    int num2;
    int index1, index2;         //交换基因时使用
    int move = 0;               //控制交叉操作的次数和对象
    while (move < popSize - 1)
    {
        pick = (float)rand() / RAND_MAX;
        // 如果随机数大于交叉概率，则不进行交叉操作，直接跳过
        if (pick > croRate)
        {
            move += 2;
            continue;
        }
        choice1 = move;
        choice2 = move + 1;
        //  随机选择两个交叉点
        pos1 = rand() % popSize;
        pos2 = rand() % popSize;
        while (pos1 > popSize - 2 || pos1 < 1)
        {
            pos1 = rand() % popSize;
        }
        while (pos2 > popSize - 2 || pos2 < 1)
        {
            pos2 = rand() % popSize;
        }
        //保证pos1比pos2小
        if (pos1 > pos2)
        {
            temp = pos1;
            pos1 = pos2;
            pos2 = temp;
        }
        //交换pos1到pos2之间的基因片段
        for (int j = pos1; j <= pos2; j++)
        {
            temp = genes[choice1].cityArr[j];
            genes[choice1].cityArr[j] = genes[choice2].cityArr[j];
            genes[choice2].cityArr[j] = temp;
        }
        //处理基因冲突问题
        num1 = 0;
        num2 = 0;

        if (pos1 > 0 && pos2 < popSize - 1)
        {
            /********** Begin **********/
            for (int j = 0; j < pos1; j++)//记录第一个交叉点之前的片段和交叉片段之间发生冲突的基因位置
            {
                for (int k = pos1; k <= pos2; k++)
                {
                    if (genes[choice1].cityArr[j] == genes[choice1].cityArr[k])
                    {
                        conflict1[num1++] = j;
                    }
                    if (genes[choice2].cityArr[j] == genes[choice2].cityArr[k])
                    {
                        conflict2[num2++] = j;
                    }
                }
            }
            /********** End **********/
            for (int j = pos2 + 1; j < popSize; j++)//记录第二个交叉点之后的片段和交叉片段之间发生冲突的基因位置
            {
                for (int k = pos1; k <= pos2; k++)
                {
                    /********** Begin **********/
                    if (genes[choice1].cityArr[j] == genes[choice1].cityArr[k])
                    {
                        conflict1[num1++] = j;
                    }
                    if (genes[choice2].cityArr[j] == genes[choice2].cityArr[k])
                    {
                        conflict2[num2++] = j;
                    }
                    /********** End **********/

                }
            }
        }
        if ((num1 == num2) && num1 > 0)//将两个冲突子代的冲突基因进行交换
        {
            for (int j = 0; j < num1; j++)
            {
                index1 = conflict1[j];
                index2 = conflict2[j];
                temp = genes[choice1].cityArr[index1];
                genes[choice1].cityArr[index1] = genes[choice2].cityArr[index2];
                genes[choice2].cityArr[index2] = temp;
            }
        }
        move += 2;
    }
}

8.void mutation()函数

变异函数的作用是在一定概率下随机交换某个物种的两个城市顺序，以增加种群的多样性

void mutation()
{
    double pick;                            //随机数
    int pos1, pos2, temp;                   //交换位置和临时变量
    for (int i = 0; i < popSize; i++)       //遍历每个种群
    {
        pick = (float)rand() / RAND_MAX;    // 生成一个0到1之间的随机数
        if (pick > mutRate)                 // 如果随机数大于变异率，则跳过该物种
        {
            continue;
        }
        pos1 = rand() % popSize;            // 随机生成第一个交换位置
        pos2 = rand() % popSize;            // 随机生成第二个交换位置
        while (pos1 > popSize - 1)          // 如果第一个位置超出范围，则重新生成
        {
            pos1 = rand() % popSize;
        }
        while (pos2 > popSize - 1)          // 如果第二个位置超出范围，则重新生成
        {
            pos2 = rand() % popSize;
        }

        int a = genes[i].dis;               // 记录原来的总距离
        temp = genes[i].cityArr[pos1];      // 交换两个城市的顺序
        genes[i].cityArr[pos1] = genes[i].cityArr[pos2];
        genes[i].cityArr[pos2] = temp;

        popFitness();                       // 计算新的适应度函数值
        if (genes[i].dis > a)               // 如果新的总距离大于原来的，则恢复原来的顺序（贪心策略）
        {
            temp = genes[i].cityArr[pos1];
            genes[i].cityArr[pos1] = genes[i].cityArr[pos2];
            genes[i].cityArr[pos2] = temp;
        }
    }
}

6.完整代码

#include "stdio.h"
#include "stdlib.h"
#include "time.h"

#define cityNum 10          //城市数量				
#define popSize 10          //种群大小
#define croRate 0.85		//交叉概率   
#define mutRate 0.1			//变异概率
#define MAX 999				//最大距离

//定义染色体的结构
struct Chrom
{
    int cityArr[cityNum];   //城市编号
    char name;              //染色体名称
    float adapt;            //个体适应度
    int dis;                //个体距离
};
struct Chrom genes[popSize];        //种群
struct Chrom genesNew[popSize];     //新种群
struct Chrom temp;


char names[cityNum] = { 'A','B','C','D','E','F','G','H','I','J' };      //城市名

int distance[cityNum][cityNum] = { { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9  },
    {  1, 0, 1, 2, 3, 4, 5, 6, 7, 8  },
    {  2, 1, 0, 1, 2, 3, 4, 5, 6, 7  },
    {  3, 2, 1, 0, 1, 2, 3, 4, 5, 6  },
    {  4, 3, 2, 1, 0, 1, 2, 3, 4, 5  },
    {  5, 4, 3, 2, 1, 0, 1, 2, 3, 4  },
    {  6, 5, 4, 3, 2, 1, 0, 1, 2, 3  },
    {  7, 6, 5, 4, 3, 2, 1, 0, 1, 2  },
    {  8, 7, 6, 5, 4, 3, 2, 1, 0, 1  },
    {  9, 8, 7, 6, 5, 4, 3, 2, 1, 0  }
};     //距离邻接矩阵

//初始化群体，生成一组随机的染色体
void initGroup()
{
    int i, j, k;
    int t = 0;
    int flag = 0;
    srand(time(NULL));                  //用于初始化随机数种子，time(NULL)返回当前系统时间
    for (i = 0; i < popSize; i++)       //每次生成一个染色体
    {

        temp.name = names[i];           //定义temp结构体，记录染色体的名称、适应度和距离
        temp.adapt = 0.0f;
        temp.dis = 0;

        for (j = 0; j < cityNum;)
        {
            t = rand() % cityNum;       //每次在城市列表中随机选取一个城市编号
            flag = 1;
            for (k = 0; k < j; k++)
            {
                if (genes[i].cityArr[k] == t)   //判断选取的城市是否已经被选中
                {
                    flag = 0;
                    break;
                }
            }
            if (flag)                   //选取的城市没有被选中
            {
                temp.cityArr[j] = t;    //存入数组中
                genes[i] = temp;        //生成一个完整的染色体
                j++;                    //j自增1
            }
        }
    }
}

void popFitness()       //计算种群中每个个体的适应度值
{
    int i, n1, n2;
    for (i = 0; i < popSize; i++)       //循环遍历种群中的所有个体
    {
        genes[i].dis = 0;               //初始化当前个体的路径长度为0
        for (int j = 1; j < cityNum; j++)       //循环遍历当前个体中所有的城市
        {
            n1 = genes[i].cityArr[j - 1];       //获取前一个城市的编号
            n2 = genes[i].cityArr[j];           //获取当前城市的编号
            genes[i].dis += distance[n1][n2];   //将前一个城市到当前城市的距离累加到路径长度中
        }
        //将最后一个城市到第一个城市的距离加到路径长度中，得到该个体的总路径长度
        genes[i].dis += distance[genes[i].cityArr[0]][genes[i].cityArr[cityNum - 1]];
        //计算当前个体的适应度值，并保存到genes数组中
        genes[i].adapt = (float)1 / genes[i].dis;
    }
}

//从种群中选择适应度最高的个体
int chooseBest()
{
    int choose = 0;         //适应度最高的个体的索引
    float best = 0.0f;      //当前适应度最高的值
    best = genes[0].adapt;  //初始化当前适应度最高的值
    for (int i = 0; i < popSize; i++)
    {
        if (genes[i].adapt < best)      //如果当前个体的适应度值比当前适应度最高的值还小
        {
            best = genes[i].adapt;      //更新当前适应度最高的值
            choose = i;                 //更新适应度最高的个体的索引
        }
    }
    return choose;          //返回适应度最高的个体的索引
}

void select()
{
    float biggestSum = 0.0f;            //定义适应度总和
    float adapt_pro[popSize];
    float pick = 0.0f;
    int i;
    for (i = 0; i < popSize; i++)       //计算适应度总和
    {
        biggestSum += genes[i].adapt;
    }
    for (i = 0; i < popSize; i++)       //计算每个个体的适应度占总适应度的比例
    {
        adapt_pro[i] = genes[i].adapt / biggestSum;
    }

    for (i = 0; i < popSize; i++)
    {
        pick = (float)rand() / RAND_MAX;    //随机选择一个个体
        /********** Begin **********/
        float sum = 0.0f;
        for (int j = 0; j < popSize; j++)
        {
            sum += adapt_pro[j];       //累加适应度比例
            if (sum > pick)            //当累加值超过pick时，选择对应的个体
            {
                genesNew[i] = genes[j];
                break;
            }
        }
        /********** End **********/
    }
    for (i = 0; i < popSize; i++)       //将新生成的种群genesNew复制到原来的genes数组中，以更新种群
    {
        genes[i] = genesNew[i];
    }
}

void cross()
{
    float pick;
    int choice1, choice2;       //交叉的两个父代
    int pos1, pos2;             //记录交叉点位置
    int temp;
    int conflict1[popSize];     //记录父代1的冲突基因位置
    int conflict2[popSize];     //记录父代2的冲突基因位置
    int num1;                   //num用来记录冲突基因个数，且两个父代冲突基因数相同
    int num2;
    int index1, index2;         //交换基因时使用
    int move = 0;               //控制交叉操作的次数和对象
    while (move < popSize - 1)
    {
        pick = (float)rand() / RAND_MAX;
        // 如果随机数大于交叉概率，则不进行交叉操作，直接跳过
        if (pick > croRate)
        {
            move += 2;
            continue;
        }
        choice1 = move;
        choice2 = move + 1;
        //  随机选择两个交叉点
        pos1 = rand() % popSize;
        pos2 = rand() % popSize;
        while (pos1 > popSize - 2 || pos1 < 1)
        {
            pos1 = rand() % popSize;
        }
        while (pos2 > popSize - 2 || pos2 < 1)
        {
            pos2 = rand() % popSize;
        }
        //保证pos1比pos2小
        if (pos1 > pos2)
        {
            temp = pos1;
            pos1 = pos2;
            pos2 = temp;
        }
        //交换pos1到pos2之间的基因片段
        for (int j = pos1; j <= pos2; j++)
        {
            temp = genes[choice1].cityArr[j];
            genes[choice1].cityArr[j] = genes[choice2].cityArr[j];
            genes[choice2].cityArr[j] = temp;
        }
        //处理基因冲突问题
        num1 = 0;
        num2 = 0;

        if (pos1 > 0 && pos2 < popSize - 1)
        {
            /********** Begin **********/
            for (int j = 0; j < pos1; j++)//记录第一个交叉点之前的片段和交叉片段之间发生冲突的基因位置
            {
                for (int k = pos1; k <= pos2; k++)
                {
                    if (genes[choice1].cityArr[j] == genes[choice1].cityArr[k])
                    {
                        conflict1[num1++] = j;
                    }
                    if (genes[choice2].cityArr[j] == genes[choice2].cityArr[k])
                    {
                        conflict2[num2++] = j;
                    }
                }
            }
            /********** End **********/
            for (int j = pos2 + 1; j < popSize; j++)//记录第二个交叉点之后的片段和交叉片段之间发生冲突的基因位置
            {
                for (int k = pos1; k <= pos2; k++)
                {
                    /********** Begin **********/
                    if (genes[choice1].cityArr[j] == genes[choice1].cityArr[k])
                    {
                        conflict1[num1++] = j;
                    }
                    if (genes[choice2].cityArr[j] == genes[choice2].cityArr[k])
                    {
                        conflict2[num2++] = j;
                    }
                    /********** End **********/

                }
            }
        }
        if ((num1 == num2) && num1 > 0)//将两个冲突子代的冲突基因进行交换
        {
            for (int j = 0; j < num1; j++)
            {
                index1 = conflict1[j];
                index2 = conflict2[j];
                temp = genes[choice1].cityArr[index1];
                genes[choice1].cityArr[index1] = genes[choice2].cityArr[index2];
                genes[choice2].cityArr[index2] = temp;
            }
        }
        move += 2;
    }
}

void mutation()
{
    double pick;                            //随机数
    int pos1, pos2, temp;                   //交换位置和临时变量
    for (int i = 0; i < popSize; i++)       //遍历每个种群
    {
        pick = (float)rand() / RAND_MAX;    // 生成一个0到1之间的随机数
        if (pick > mutRate)                 // 如果随机数大于变异率，则跳过该物种
        {
            continue;
        }
        pos1 = rand() % popSize;            // 随机生成第一个交换位置
        pos2 = rand() % popSize;            // 随机生成第二个交换位置
        while (pos1 > popSize - 1)          // 如果第一个位置超出范围，则重新生成
        {
            pos1 = rand() % popSize;
        }
        while (pos2 > popSize - 1)          // 如果第二个位置超出范围，则重新生成
        {
            pos2 = rand() % popSize;
        }

        int a = genes[i].dis;               // 记录原来的总距离
        temp = genes[i].cityArr[pos1];      // 交换两个城市的顺序
        genes[i].cityArr[pos1] = genes[i].cityArr[pos2];
        genes[i].cityArr[pos2] = temp;

        popFitness();                       // 计算新的适应度函数值
        if (genes[i].dis > a)               // 如果新的总距离大于原来的，则恢复原来的顺序（贪心策略）
        {
            temp = genes[i].cityArr[pos1];
            genes[i].cityArr[pos1] = genes[i].cityArr[pos2];
            genes[i].cityArr[pos2] = temp;
        }
    }
}

int main()
{
    char c = 0;
    //printf("\n\t\t******************************** ÒÅ´«Ëã·¨Çó½âTSP(ÂÃÐÐÉÌ)ÎÊÌâ *********************************\n");
    initGroup();	//³õʼ»¯
    popFitness();	//¸üÐÂÊý¾Ý
    //Êä³öÅäÖÃÐÅÏ¢
    /*printf("\n\t\t»ùÒò³¤¶È:%d",cityNum);
    printf("\tÖÖȺ´óС:%d",popSize);
    printf("\t½»²æ¸ÅÂÊ:%.2f",croRate);
    printf("\t±äÒì¸ÅÂÊ:%.2f",mutRate);
    printf("\t½ø»¯´úÊý:%d",MAX);
    printf("\tÔ¤Éè×îÓŽ⣺18");
    printf("\n\n\t\t**********************************************************************************************\n");*/

    int i, j;
    //Êä³ö¾àÀë¾ØÕó
    /*printf("\n\t\t--------- ³ÇÊоàÀë¾ØÕó ---------\n");
    printf("\t\t");
    int i,j;
    for(i = 0; i < cityNum; i ++)
    {
        for(j = 0;j < cityNum; j ++)
        {
            printf("  %d",distance[i][j]);
        }
        printf("\n\t\t");
    }
    printf("--------------------------------");*/

    //Êä³ö·¾¶ÐÅÏ¢
    /*printf("\n\t\t-------- ³õʼÖÖȺ»ùÒò¿â --------\n");
    printf("\t\t ");

    for(i = 0; i < cityNum; i ++)
    {
        printf("  %c",genes[i].name);
    }
    printf("\n\t\t");
    for(i = 0;i < cityNum; i ++)
    {
        printf("%c",genes[i].name);
        for(j = 0; j < cityNum; j ++)
        {
            printf("  %d",genes[i].cityArr[j]);
        }
        printf("\n\t\t");
    }
    printf("--------------------------------\n");*/


    //printf("\n\t\tÑ°Çó×îÓŽâÖУº");
    //ͨ¹ý²»¶Ï½ø»¯£¬Ö±µ½´ïµ½¶¨ÒåµÄ½ø»¯´úÊý
    for (i = 0; i < MAX; i++)
    {
        select();
        cross();
        mutation();
        popFitness();//¸üÐÂÊý¾Ý
        int temp = (int)MAX / 20;
        /*if( i % temp == 0)
        {
            //printf("¨‚");
            Sleep(200);
        }*/
    }
    //printf("Íê³É");
    //printf("\n\n\t\t×îÓÅ·¾¶£º");
    /*for(i = 0; i < cityNum ; i++)
    {
        printf("%d-->",genes[chooseBest()].cityArr[i]);
    }
    printf("%d",genes[chooseBest()].cityArr[0]);*/
    printf("%d", genes[chooseBest()].dis);
    //printf("\n\n\t\tÊÇ·ñÔÙÊÔÒ»´Î?(Y/y) ÊÇ/(N/n) ·ñ£º");
    fflush(stdin);
    /* c = getchar();
     fflush(stdin);
     if(c=='N'||c=='n')
     {
         break;
     }*/

     //printf("\n\t\t");
    return 0;
}

运行结果：

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/402828.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Kaggle赛题解析：Diffusion Prompt生成

Kaggle赛题解析：Diffusion Prompt生成

文章目录一、比赛信息二、比赛背景三、比赛任务四、评价指标五、数据描述六、解题思路一、比赛信息 比赛名称&#xff1a;Stable Diffusion - Image to Prompts 推断生成高度详细、清晰的焦点、插图、宏伟、史诗般的 3d 渲染图像的prompt 比赛链接&#xff1a;https://www.k…
阅读更多...
python----获取一部小说

python----获取一部小说

1、需求说明 获取一部小说的标题内容&#xff0c;以txt文档形式保存 2、项目说明 3、代码 # 怎么发送请求 # pip install requests import requests# pip install lxml->从标签里提起文字 #from lxml import etree from lxml import html etreehtml.etree # 发送给谁 url…
阅读更多...
Android---系统启动流程

Android---系统启动流程

目录 Android 系统启动流程 init 进程分析 init.rc 解析 Zygote 概叙 Zygote 触发过程 Zygote 启动过程 什么时Runtime&#xff1f; System Server 启动流程 Fork 函数 总结 面试题 Android 是 google 公司开发的一款基于 Linux 的开源操作系统。 Android 系统启动…
阅读更多...
Web3中文｜一波未平一波又起：Silvergate将走向何处

Web3中文｜一波未平一波又起：Silvergate将走向何处

Silvergate Capital&#xff08;SI&#xff09;这一加密公司曾经的重要银行合作伙伴&#xff0c;现在正处于崩溃的边缘。这家总部位于加州拉荷亚的公司上周五晚上表示&#xff0c;其暂停了Silvergate交易所网络&#xff08;SEN&#xff1a;Silvergate Exchange Network&#xf…
阅读更多...
Foxit PDF SDK ActiveX 5.9.7 Crack

Foxit PDF SDK ActiveX 5.9.7 Crack

Foxit PDF SDK ActiveX对于刚接触PDF或不愿投入过多精力学习PDF技术的产品管理者及开发者来说&#xff0c;Foxit PDF SDK ActiveX无疑是理想的选择。破解版它拥有操作简单的特性&#xff0c;提供可支持定制的可视化编程组件&#xff0c;开发者通过简单的拖放动作&#xff0c;就…
阅读更多...
扬帆配资|建筑业景气度持续回升，多只概念股业绩有望增长

扬帆配资|建筑业景气度持续回升，多只概念股业绩有望增长

新式城镇化概念股遭到商场重视。 今天早盘&#xff0c;新式城镇化概念股冲高&#xff0c;恒锋信息、ST花王涨停。蕾奥规划、筑博规划一度冲高至15%&#xff0c;冠龙节能、杭州园林、美晨生态跟涨。 国家出台一系列城镇化相关方针 城镇化&#xff0c;是人口向城镇会集的进程。…
阅读更多...
【Kubernetes】第二十三篇 - 布署 nodejs 后端项目（上）

【Kubernetes】第二十三篇 - 布署 nodejs 后端项目（上）

一&#xff0c;前言 上一篇&#xff0c;介绍了 MySQL 服务的部署&#xff1b; 本篇&#xff0c;介绍 nodejs 后端项目的布署&#xff08;将后端项目构建成为 docker 镜像&#xff0c;并推送至镜像仓库&#xff09;&#xff1b; 二&#xff0c;准备项目 创建后端项目&#xf…
阅读更多...
8、LSM树

8、LSM树

一、前言 最近在调研NoSQL数据库&#xff0c;发现RocksDB、LevelDB、HBase以及Prometheus等&#xff0c;其底层的存储引擎都是基于LSM树&#xff0c;于是决定花时间彻底吃透LSM树这一数据结构。 不幸的是&#xff0c;在查阅资料学习的过程中&#xff0c;发现网上各种文章汗牛…
阅读更多...
浅谈对Promise的理解以及在工作中的应用

浅谈对Promise的理解以及在工作中的应用

浅谈对Promise的理解以及在工作中的应用Promise的概念背景知识JavaScript的同步和异步JavaScript事件循环回调函数进行异步操作解决方案&#xff1a;PromisePromise 在工作中的运用创建PromisePromise封装AJAXPromise链式操作Promise.all()Promise.race()async和await总结Promi…
阅读更多...
轻松转换文档：antennahouse/Office Server Document Converter

轻松转换文档：antennahouse/Office Server Document Converter

关于 Office Server 文档转换器 (OSDC)破解版 无需 Microsoft Office 或 Adob​​e 软件即可快速准确地转换文档。 Office Server 文档转换器 (OSDC) 会将您在 Microsoft Office&#xff08;Word、Excel、PowerPoint&#xff09;中创建的重要文档转换为高质量的 PDF 或图像格式…
阅读更多...
国内32位MCU在电机控制上的应用方案

国内32位MCU在电机控制上的应用方案

电机&#xff08;Electric machinery&#xff0c;俗称“马达”&#xff09;是依据电磁感应定律&#xff0c;实现电能转换或传递的一种电磁装置&#xff0c;其主要作用是产生驱动转矩&#xff0c;为用电器或各类机械提供动力。电机作为工业世界的动力之源&#xff0c;几乎用于所…
阅读更多...
ThinkPHP 6.1 模板篇之布局与继承

ThinkPHP 6.1 模板篇之布局与继承

本文主要讲述ThinkPHP 6.1版本模板几种布局的方法和如何实现继承&#xff0c; 可以与《ThinkPHP 6.1 模板篇之文件加载》结合来看。 模板布局 布局方式有两种可以实现。 布局方法1 开启配置 默认情况下&#xff0c;不支持模版布局功能&#xff0c;需要在配置文件中开启&…
阅读更多...
如何快速通过PMP考试？

如何快速通过PMP考试？

我建议准备的最短时间至少一个月&#xff0c;我用了一个半月&#xff0c;我每天集中精力备考大约4个小时&#xff0c;大家可以根据自己的专注力的长短去调节每天的备考时间。 准备5月的&#xff0c;还没备考的&#xff0c;现在开始也来得及。5月没有报名的可以准备8月的&#…
阅读更多...
【Linux系统编程】05：多进程

【Linux系统编程】05：多进程

多进程 OVERVIEW多进程一、进程创建1.创建1个子进程2.创建多个子进程二、进程控制1.进程结束2.进程等待3.子进程操作14.子进程操作2三、进程体系1.守护进程2.进程调度程序&#xff1a;一种已经编译好的、存在磁盘中的二进制文件&#xff08;脚本为普通文件&#xff09;。进程&a…
阅读更多...
超图iServer扩展开发记录Restlet 3

超图iServer扩展开发记录Restlet 3

HTTP 请求在达到 REST 应用对象&#xff0c;交给资源实现类处理的时候&#xff0c;先要解析 HTTP 请求中的参数&#xff0c;然后才会进入业务逻辑进行处理。参数解析的工作由参数解析器&#xff08;Decoder&#xff09;进行&#xff0c;即可以实现将请求参数转换为 Java 对象。…
阅读更多...
qt tcp通讯

qt tcp通讯

TCP 协议&#xff08;Transmission Control Protocol&#xff09;全称是传输控制协议是一种面向连接的、可靠的、基于字节流的传输层通信协议。tcp服务端使用QTcpServer、QTcpSocket。tcp客户端使用QTcpSocket1.在工程文件(工程文件.pro)中的第一行添加network 如QT core gui …
阅读更多...
WeSpeaker支持C++部署链路

WeSpeaker支持C++部署链路

WeSpeaker正式更新C部署链路&#xff0c;推理引擎使用OnnxRuntime&#xff0c;支持从语音中提取Speaker Embedding信息&#xff0c;代码详见WeSpeaker/runtime[1]。 Libtorch和onnx的选择? Speaker Embedding提取任务流程简单&#xff0c;并且声纹模型&#xff08;如ResNet\E…
阅读更多...
前端js学习

前端js学习

1. js入门 1.1 js是弱类型语言 1.2 js使用方式 1.2.1 在script中写 1.2.2 引入js文件 1.2.3 优先级 1.3 js查错方式 1.4 js变量定义 1.4 js数据类型 数据类型英文表示示例数值类型number1.1 1字符串类型string‘a’ ‘abc’ “abc”对象类型object布尔类型booleannumber函数…
阅读更多...
包教包会的Node.js

包教包会的Node.js

一、简介 1、什么是Node.js 简单的说 Node.js 就是运行在服务端的 JavaScript。 Node.js是一个事件驱动I/O服务端JavaScript环境&#xff0c;基于Google的V8引擎&#xff0c;V8引擎执行Javascript的速度非常快&#xff0c;性能非常好。 2、Node.js有什么用 如果你是一个前…
阅读更多...
风起|微软突发声明：始终严格保护并捍卫用户隐私

风起|微软突发声明：始终严格保护并捍卫用户隐私

开放隐私计算 3 月 9 日消息&#xff0c;微软中国今天发布了声明&#xff0c;针对日前国内某些自媒体传播的有关个人用户使用微软消费类产品和服务的误解&#xff0c;特做了相关说明。微软表示&#xff0c;微软始终严格遵守个人隐私保护与数据安全等方面的各项法律法规。微软提…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023