【算法数据结构体系篇class16】：图拓扑排序

一、图

1）由点的集合和边的集合构成

2）虽然存在有向图和无向图的概念，但实际上都可以用有向图来表达

3）边上可能带有权值

二、图结构的表达

1）邻接表法类似哈希表, key就是当前节点。value就是对应有指向的邻接节点

2）邻接矩阵法类似二维数据横纵分别都是节点，每个[i][j]表示i j 两点的连接

3）除此之外还有其他众多的方式

三、图的题目如何搞定

图的算法都不算难，只不过coding的代价比较高

1）先用自己最熟练的方式，实现图结构的表达

2）在自己熟悉的结构上，实现所有常用的图算法作为模板

3）把题提供的图结构转化为自己熟悉的图结构，再调用模板或改写即可

四、点、边、图定义类、二维数组信息转换图结构

package class16;

import java.util.ArrayList;
import java.util.List;

//节点类结构
public class NodeTrain {
    public int value;                 //节点值
    public int in;                    //入度  即指向该节点的前节点个数
    public int out;                   //出度  即从该节点指向的后节点个数
    public List<NodeTrain> nexts;    //该节点指向的后节点集合
    public List<EdgeTrain> edges;         //从该节点指向后节点的边
    public NodeTrain(int v){
        value = v;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }
}

package class16;

//两节点相连的边结构类
public class EdgeTrain {
    public int weight;               //边权重
    public NodeTrain from;           //该边的起始节点  from -> to
    public NodeTrain to;             //该边的终止节点
    public EdgeTrain(int w,NodeTrain f, NodeTrain t){
        weight = w;
        from = f;
        to = t;
    }
}

package class16;

import java.util.HashMap;
import java.util.HashSet;
import java.util.List;

//图结构类，包含了图中的节点，节点之间的边
public class GraphTrain {
    public HashMap<Integer,NodeTrain> nodes;       //图中的节点 key表示节点值 value表示 对应值封装的节点类结构
    public HashSet<EdgeTrain> edges;                    //图中的边
    public GraphTrain(){
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }
}

package class16;

public class GraphGeneratorTrain {
    // matrix 所有的边
    // N*3 的矩阵
    // [weight, from节点上面的值，to节点上面的值]
    //
    // [ 5 , 0 , 7]
    // [ 3 , 0,  1]
    //
    public static GraphTrain createGraph(int[][] matrix) {
        GraphTrain graphTrain = new GraphTrain();
        //将二维数组信息 分别取出 边权重 起始节点 终止节点
        for (int i = 0; i < matrix.length; i++) {
            //每一行就是一组节点数组 取出对应值
            int weight = matrix[i][0];
            int fromV = matrix[i][1];
            int toV = matrix[i][2];
            //判断该两节点是否不在图类中的nodes集合 不在那么就添加进去
            if(!graphTrain.nodes.containsKey(fromV)){
                graphTrain.nodes.put(fromV,new NodeTrain(fromV));
            }
            if(!graphTrain.nodes.containsKey(toV)){
                graphTrain.nodes.put(toV,new NodeTrain(toV));
            }
            //接着就是添加两节点的边 取出两个节点
            NodeTrain fromNode = graphTrain.nodes.get(fromV);
            NodeTrain toNode = graphTrain.nodes.get(toV);
            EdgeTrain edgeTrain = new EdgeTrain(weight, fromNode, toNode);
            //图添加边  起始节点的指向节点集合添加终止节点 出度+1  终止节点入度+1 起始节点的边集合添加该边
            graphTrain.edges.add(edgeTrain);
            fromNode.nexts.add(toNode);
            fromNode.out++;
            toNode.in++;
            fromNode.edges.add(edgeTrain);
        }
        return graphTrain;
    }
}

五、图的宽度优先&深度优先遍历

宽度优先遍历

1，利用队列实现
2，从源节点开始依次按照宽度进队列，然后弹出
3，每弹出一个点，把该节点所有没有进过队列的邻接点放入队列
4，直到队列变空

深度优先遍历

1，利用栈实现
2，从源节点开始把节点按照深度放入栈，然后弹出
3，每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈
4，直到栈变空

package class16;

import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;

/**
 * 图宽度优先遍历
 * 1，利用队列实现
 * 2，从源节点开始依次按照宽度进队列，然后弹出
 * 3，每弹出一个点，把该节点所有没有进过队列的邻接点放入队列
 * 4，直到队列变空
 */

public class BFS {
    //从start节点开始 进行宽度优先遍历
    public void bfs(NodeTrain start){
        if(start == null){    //空节点就直接返回
            return;
        }
        //定义队列，将开始节点入队列，后续用来遍历
        Queue<NodeTrain> queue = new LinkedList<>();
        queue.add(start);
        //定义有序集合，将开始节点入队列，目的是为了避免图中多个指向一个节点的情况，就需要判断存在就不需遍历，否则会存在重复打印或者死循环
        HashSet<NodeTrain> set = new HashSet<>();
        set.add(start);
        while(!queue.isEmpty()){
            //先弹出队列节点 并打印
            NodeTrain poll = queue.poll();
            System.out.println(poll.value);
            //判断当前节点的下层指向节点
            for(NodeTrain next:poll.nexts){
                //如果当前的有序集合中 不存在该下层节点时，那么就可以入队列，入有序集合 用于后续的弹出以及避免再打印
                if(!set.contains(next)){
                    queue.add(next);
                    set.add(next);
                }
            }
        }
    }

}

package class16;

import java.util.HashSet;
import java.util.Stack;

/**
 * 图深度优先遍历
 * 1，利用栈实现
 * 2，从源节点开始把节点按照深度放入栈，然后弹出
 * 3，每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈,一旦有入栈，注意就要把该节点和邻接节点一起入栈。然后直接退出当前循环
 * 4，直到栈变空
 */
public class DFS {
    public void dfs(NodeTrain start){
        if(start == null){
            return ;
        }
        //定义一个栈用来存在节点 ,开始节点入栈 用于后续的遍历
        Stack<NodeTrain> stack = new Stack<>();
        stack.add(start);
        //定义一个有序集合，开始节点入集合  用于后续遍历不重复打印有多个指向的邻接节点
        HashSet<NodeTrain> set = new HashSet<>();
        set.add(start);
        //先进行打印
        System.out.println(start.value);
        while(!stack.isEmpty()){
            //弹出栈节点
            NodeTrain pop = stack.pop();
            for(NodeTrain next : pop.nexts){
                //判断该节点的下层节点是否已经在有序集合中 不在那么就需要 将当前节点与下层节点一起入栈，入集合 当前节点也需要重新入是因为要保存节点，假设还有其他的 邻接节点 后续往上往返时就可以取到节点
                if(!set.contains(next)){
                    stack.push(pop);
                    stack.push(next);
                    set.add(next);
                    //入栈后就直接打印，这样就是直接打印下层邻接节点
                    //最后打印到最后一个节点时，因为我们每次都是将上层的节点也入栈，最终整个栈保存的就是完整的一次深度优先遍历的
                    //整个链条节点，依次往上弹出，因为都入集合了，索引就不会再执行打印，直接有其他下层邻接点没有入集合的，就会进入
                    //这个节点 入栈，入集合，打印。 循环往返直至整个图的节点都打印完，栈也就为空了
                    System.out.println(next.value);
                    //因为是DFS深度优先，有一个下层节点，入栈后就退出循环，不需要再入栈同层下层节点
                    break;
                }
            }
        }
    }
}

六、图的拓扑排序算法

1）在图中找到所有入度为0的点输出
2）把所有入度为0的点在图中删掉，继续找入度为0的点输出，周而复始
3）图的所有点都被删除后，依次输出的顺序就是拓扑排序

要求：有向图且其中没有环
应用：事件安排、编译顺序

package class16;


import java.util.*;

/**
 * 自定义图的拓扑排序
 * 1）在图中找到所有入度为0的点输出
 * 2）把所有入度为0的点在图中删掉，继续找入度为0的点输出，周而复始
 * 3）图的所有点都被删除后，依次输出的顺序就是拓扑排序
 *
 * 要求：有向图且其中没有环
 * 应用：事件安排、编译顺序
 */
public class TopologySort {
    // directed graph and no loop
    public static List<NodeTrain> sortedTopology(GraphTrain graph) {
        //定义一个哈希表 存在每个节点对应的入度数
        HashMap<NodeTrain,Integer> inMap = new HashMap<>();
        //定义一个队列存在入度为0的节点，用于后续的遍历输出 图拓扑排序 就是入度0的节点排在前面
        Queue<NodeTrain> zeroQueue = new LinkedList<>();
        for(NodeTrain node: graph.nodes.values()){
            inMap.put(node,node.in);
            if(node.in == 0){
                zeroQueue.add(node);
            }
        }
        //定义一个结果集合，用来接收zeroQueue弹出的节点
        List<NodeTrain> ans = new ArrayList<>();
        //开始遍历zeroQueue队列
        while(!zeroQueue.isEmpty()){
            NodeTrain poll = zeroQueue.poll();
            //弹出的元素，就是入度0的 直接入结果集合 这个就是拓扑排序顺序
            ans.add(poll);
            //弹出后，需要刷新其邻接节点的入度数-1
            for(NodeTrain next:poll.nexts){
                inMap.put(next,inMap.get(next)-1);
                //-1后 会有些邻接节点入度变成0 这个时候需要再入队列中 用于后续弹出 放到结果集
                if(next.in == 0){
                    zeroQueue.add(next);
                }
            }
        }
        return ans;
    }
}

七、lintCode 127拓扑排序

lintCode 127拓扑排序

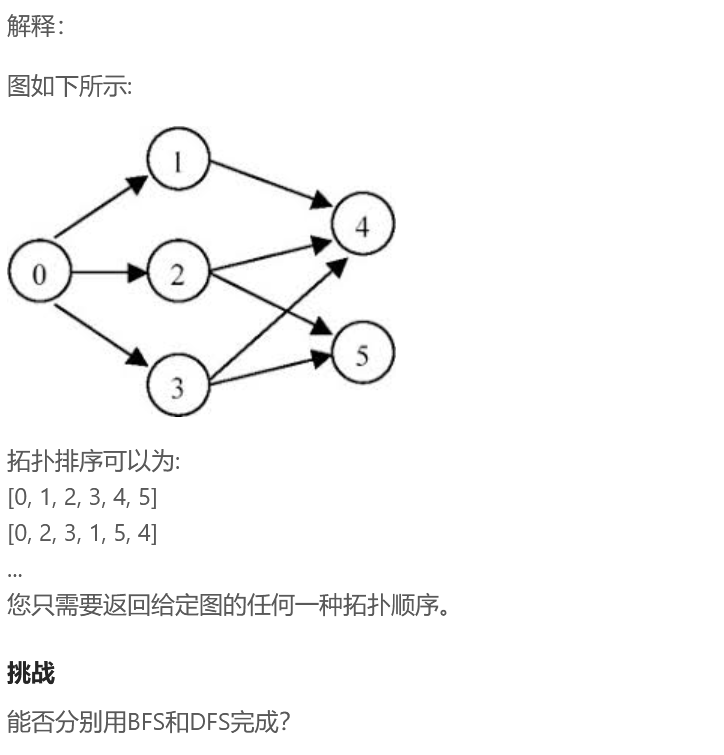
* 思路1：BFS 宽度优先遍历
* 1）在图中找到所有入度为0的点输出
* 2）把所有入度为0的点在图中删掉，继续找入度为0的点输出，周而复始
* 3）图的所有点都被删除后，依次输出的顺序就是拓扑排序

package class16;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Queue;

/**
 * 图的拓扑排序算法
 * OJ链接：https://www.lintcode.com/problem/topological-sorting
 * 描述
 *
 * 给定一个有向图，图节点的拓扑排序定义如下:
 *
 *     对于图中的每一条有向边 A -> B , 在拓扑排序中A一定在B之前.
 *     拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.
 *
 * 针对给定的有向图找到任意一种拓扑排序的顺序.
 *
 *
 * 思路：BFS 宽度优先遍历
 * 1）在图中找到所有入度为0的点输出
 * 2）把所有入度为0的点在图中删掉，继续找入度为0的点输出，周而复始
 * 3）图的所有点都被删除后，依次输出的顺序就是拓扑排序
 *
 * 要求：有向图且其中没有环
 * 应用：事件安排、编译顺序
 */
public class TopologicalOrderBFS {
    // 不要提交这个类
    public static class DirectedGraphNode {
        public int label;
        public ArrayList<DirectedGraphNode> neighbors;

        public DirectedGraphNode(int x) {
            label = x;
            neighbors = new ArrayList<DirectedGraphNode>();
        }
    }

    //方法：通过BFS宽度优先遍历来对有向图进行拓扑排序
    public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
        //找出入度为0 的节点 这里我们用哈希表存放每个节点的入度情况
        //定义节点入度哈希表 遍历节点集合 初始值value为0
        HashMap<DirectedGraphNode,Integer> inMap = new HashMap<>();
        for(DirectedGraphNode node: graph){
            inMap.put(node,0);
        }
        //再遍历集合节点的每个邻接点,将存在有邻接点，将该邻接点的入度+1
        for(DirectedGraphNode node : graph){
            for(DirectedGraphNode next : node.neighbors){
                inMap.put(next,inMap.get(next)+1);
            }
        }
        //当前我们就把inMap每个节点的入度数都确认好了。 依次取数入度为0的节点存放到一个集合中,后续用于遍历 依次取出就是图的拓扑排序
        Queue<DirectedGraphNode> zeroQueue = new LinkedList<>();
        for(DirectedGraphNode node : inMap.keySet()){
            if(inMap.get(node) == 0){
                zeroQueue.add(node);
            }
        }

        //定义结果集 依次弹出zeroQueue 入度为0 的节点 入集合，就是拓扑排序  顺序就是入度0的开始指向
        ArrayList<DirectedGraphNode> ans = new ArrayList<>();
        //开始遍历入度为0的队列
        while(!zeroQueue.isEmpty()){
            //弹出入度0的节点，并且入集合
            DirectedGraphNode poll = zeroQueue.poll();
            ans.add(poll);
            //接着需要剔除这个节点，也就是将该节点的邻接点的入度-1
            for(DirectedGraphNode next:poll.neighbors){
                inMap.put(next,inMap.get(next)-1);
                //邻接点入度-1之后 判断入度0的邻接节点 再将节点入队列
                if(inMap.get(next) == 0){
                    zeroQueue.add(next);
                }
            }
        }
        return ans;
    }

}

**思路2：DFS 深度优先遍历定义节点类包含节点对象和节点深度
* 1.深度遍历每个节点的深度比如最后的节点：没有邻接点的节点其深度为1 而指向该节点的上层节点，深度为2...
* 得到每个节点对应的深度
* 2.按节点的深度降序排序，然后依次输出节点就是图拓扑排序
* 要求：有向图且其中没有环
* 应用：事件安排、编译顺序

package class16;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.HashMap;

/**
 * 图的拓扑排序算法
 * OJ链接：https://www.lintcode.com/problem/topological-sorting
 * 描述
 * <p>
 * 给定一个有向图，图节点的拓扑排序定义如下:
 * <p>
 * 对于图中的每一条有向边 A -> B , 在拓扑排序中A一定在B之前.
 * 拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.
 * <p>
 * 针对给定的有向图找到任意一种拓扑排序的顺序.
 * <p>
 * <p>
 * 思路：DFS 深度优先遍历  定义节点类包含节点对象和节点深度
 * <p>
 * 1.深度遍历 每个节点的深度  比如最后的节点：没有邻接点的节点 其深度为1 而指向该节点的上层节点，深度为2...
 * 得到每个节点对应的深度
 * 2.按节点的深度降序排序，然后依次输出节点 就是图拓扑排序
 * <p>
 * 要求：有向图且其中没有环
 * 应用：事件安排、编译顺序
 */
public class TopologicalOrderDFS1 {
    // 不要提交这个类
    public static class DirectedGraphNode {
        public int label;
        public ArrayList<DirectedGraphNode> neighbors;

        public DirectedGraphNode(int x) {
            label = x;
            neighbors = new ArrayList<DirectedGraphNode>();
        }
    }

    //定义一个节点深度类，包含节点类信息，该节点的深度 用来最后按深度降序排序输出 得到图拓扑顺序
    public static class NodeDeep{
        public DirectedGraphNode node;   //题目定义的节点类
        public int deep;                 //该节点所在的深度
        public NodeDeep(DirectedGraphNode n,int d){
            node = n;
            deep = d;
        }
    }

    public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
        //定义哈希表     DirectedGraphNode:NodeDeep  节点做键，节点深度类做值
        HashMap<DirectedGraphNode,NodeDeep> map = new HashMap<>();
        for(DirectedGraphNode cur: graph){
            //进行递归操作 将每个节点的深度类信息添加好哈希表中
            dfs(cur,map);
        }
        //将哈希表的value遍历保存到集合中
        ArrayList<NodeDeep> list = new ArrayList<>();
        for(NodeDeep node:map.values()){
            list.add(node);
        }
        //将集合中的深度类信息按深度进行降序，降序完成，按序输出就是图的拓扑顺序
        list.sort(new Comparator<NodeDeep>(){
            public int compare(NodeDeep o1,NodeDeep o2){
                return o2.deep - o1.deep;
            }
        });
        ArrayList<DirectedGraphNode> ans = new ArrayList<>();
        for(NodeDeep node:list){
            ans.add(node.node);
        }
        return ans;
    }

    //深度优先遍历：传入一个节点，以及上面程序定义的一个哈希表记录 这个节点对应的深度
    public static NodeDeep dfs(DirectedGraphNode cur,HashMap<DirectedGraphNode,NodeDeep> map){
           if(map.containsKey(cur)){
               //如果当前哈希表没有记录该节点信息 那么就直接从表中取出返回上层
               return map.get(cur);
           }
           //定义当前类的 初始高度0 后续用来跟其邻接节点深度做比较大小 最终返回
           int deep = 0;
           //递归遍历邻接节点 取其最大的深度赋值
           for(DirectedGraphNode next:cur.neighbors){
               deep = Math.max(deep,dfs(next,map).deep);
           }
           //定义好了这两个信息后就可以创建类返回,注意deep是邻接点深度 需要+1 才是当前节点深度
           NodeDeep ans = new NodeDeep(cur,deep+1);
           //注意：还需要将这个没有在哈希表记录的节点，添加进去，后续如果又递归到该值就会直接返回 提高效率
           map.put(cur,ans);
           return new NodeDeep(cur,deep+1);
    }
}

* 思路3：DFS 深度优先遍历定义节点类包含节点对象和节点次数

* 1.深度遍历每个节点的点次数比如最后一个节点a时，点次数就是自己一个1，往上一个节点o，它有a,b,c 三个邻接节点那么它节点次数就是4
* 有指向多个节点的可以重复累计点次
* 2.按节点的点次降序排序，然后依次输出节点就是图拓扑排序

* 要求：有向图且其中没有环
* 应用：事件安排、编译顺序

package class16;

import java.util.ArrayList;
import java.util.Comparator;
import java.util.HashMap;

/**
 * 图的拓扑排序算法
 * OJ链接：https://www.lintcode.com/problem/topological-sorting
 * 描述
 * <p>
 * 给定一个有向图，图节点的拓扑排序定义如下:
 * <p>
 * 对于图中的每一条有向边 A -> B , 在拓扑排序中A一定在B之前.
 * 拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.
 * <p>
 * 针对给定的有向图找到任意一种拓扑排序的顺序.
 * <p>
 * <p>
 * 思路：DFS 深度优先遍历  定义节点类包含节点对象和节点次数
 * <p>
 * 1.深度遍历 每个节点的点次数  比如最后一个节点a时，点次数就是自己一个1，往上一个节点o，它有a,b,c 三个邻接节点 那么它节点次数就是4
 *   有指向多个节点的可以重复累计点次
 *
 * 2.按节点的点次降序排序，然后依次输出节点 就是图拓扑排序
 * <p>
 * 要求：有向图且其中没有环
 * 应用：事件安排、编译顺序
 */
public class TopologicalOrderDFS2 {
    // 不要提交这个类
    public static class DirectedGraphNode {
        public int label;
        public ArrayList<DirectedGraphNode> neighbors;

        public DirectedGraphNode(int x) {
            label = x;
            neighbors = new ArrayList<DirectedGraphNode>();
        }
    }

    //节点次数类
    public static class NodeDeep{
        public DirectedGraphNode node;
        public long size;
        public NodeDeep(DirectedGraphNode n,long s){
            node = n;
            size = s;
        }
    }
    public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
        //定义一个哈希表，存储节点类对应的节点次数类
        HashMap<DirectedGraphNode,NodeDeep> map = new HashMap<>();
        //遍历节点集合，刷新节点的节点次数类
        for(DirectedGraphNode cur:graph){
            dfs(cur,map);
        }
        //定义一个集合存放哈希表的 节点次数类
        ArrayList<NodeDeep> list = new ArrayList<>();
        for(NodeDeep node:map.values()){
            list.add(node);
        }
        //进行按次数降序排序， 就是图的拓扑排序
        list.sort(new Comparator<NodeDeep>() {
            @Override
            public int compare(NodeDeep o1, NodeDeep o2) {
                //比较器注意 因为是Long类型 所以我们要控制返回0 -1 1
                return o1.node == o2.node ? 0 : o1.size - o2.size > 0? -1:1;
            }
        });
        //定义结果集合 将集合中的节点次数类的节点类添加到集合
        ArrayList<DirectedGraphNode> ans = new ArrayList<>();
        for(NodeDeep node:list){
            ans.add(node.node);
        }
        return ans;
    }

    //递归将该节点的节点次数往下找返回其次数
    public static NodeDeep dfs(DirectedGraphNode cur,HashMap<DirectedGraphNode,NodeDeep>map){
        if(map.containsKey(cur)){
            //如果哈希表中存在该节点的记录 就直接返回
            return map.get(cur);
        }
        long size = 0;    //定义当前节点的节点次数
        for(DirectedGraphNode next:cur.neighbors){
            //遍历下层邻接点，返回其节点次数累加给当前节点
            size += dfs(next,map).size;
        }
        //定义当前节点的信息,次数要+1当前节点 并返回
        NodeDeep ans = new NodeDeep(cur,size+1);
        //注意并且要将节点信息添加到哈希表中记录 下次遍历相同节点可以直接返回
        map.put(cur,ans);
        return ans;
    }
}