介绍

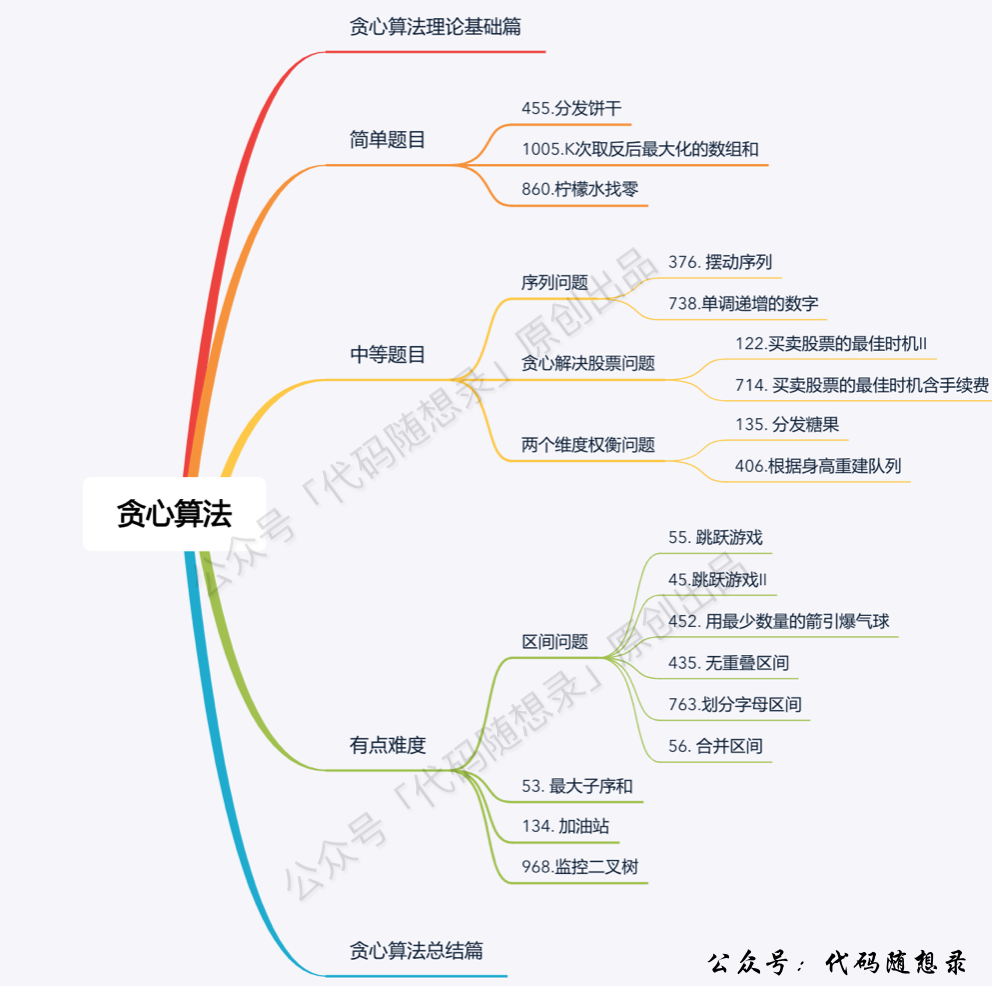
贪心算法是一种基于贪心思想的算法，它每次选择当前最优的解决方案，从而得到全局最优解。具体来说，贪心算法在每一步都做出局部最优选择，希望通过这种方式最终达到全局最优解。贪心算法通常适用于问题具有最优子结构性质和无后效性的情况。尽管贪心算法并不总是能够得到最优解，但它通常具有高效、简单等优点，并且在许多实际问题中得到了广泛应用。

一般来说，可以从以下几个方面考虑如何区别题目要使用贪心算法还是动态规划算法：

1、问题的性质：贪心算法适用于具有最优子结构性质和无后效性的问题，而动态规划算法则适用于具有重叠子问题和最优子结构性质的问题。

2、对时间复杂度的要求：贪心算法通常比动态规划算法更加高效，但并不总能得到最优解。如果对时间复杂度有较高的要求，可以首先考虑贪心算法；否则可以使用动态规划算法。

3、解决问题的方式：贪心算法通常是从局部最优解推导出全局最优解，即每次都选择当前最优解，并期望通过这种方式得到最终的最优解。而动态规划算法则是通过将问题分解成多个子问题，并保存已经求解过的子问题的结果，然后再利用这些子问题的结果求解更大的子问题，最终得到全局最优解。

4、是否存在贪心选择性质或者无后效性质：关键在于是否能够证明问题具有贪心选择性质或者无后效性质，如果问题确实具有这些性质，那么使用贪心算法也许是一个较好的选择。

在这里插入图片描述

分配饼干

https://leetcode.cn/problems/assign-cookies/description/

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort()
        s.sort()
        i, j = 0, 0
        while i < len(g) and j < len(s):
            if g[i] <= s[j]:
                i += 1
            j += 1
        return i

K 次取反后最大化的数组和

https://leetcode.cn/problems/maximize-sum-of-array-after-k-negations/description/

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组可能的最大和。

class Solution:
    def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:
        nums.sort()
        for i in range(len(nums)):
            if nums[i] < 0 and k > 0:
                nums[i] = -nums[i]
                k -= 1
            else:
                break
        nums.sort()
        if k % 2 == 1:
            nums[0] = -nums[0]
        return sum(nums)

柠檬水找零

https://leetcode.cn/problems/lemonade-change/

使用贪心算法解决该问题，具体步骤如下：
1、初始化变量 fives, tens 为 0，分别表示手中拥有的 5 元和 10 元数量。
2、对于每个顾客支付的钞票金额 bill，进行如下操作：

如果 bill 为 5 元，则不需要找零，直接将手中的 5 元数量加 1。
如果 bill 为 10 元，则需要找零 5 元，此时需要检查手中是否有足够的 5 元可找零，如果没有则返回 False；否则将手中的 10 元数量加 1，将手中的 5 元数量减 1。
如果 bill 为 20 元，则需要找零 15 元，优先使用一张 10 元和一张 5 元找零，如果手中没有足够的 10 元和 5 元，则尝试使用三张 5 元找零，如果还是无法找零，则返回 False。

3、如果成功为所有顾客找到了零钱，则返回 True。

class Solution:
    def lemonadeChange(self, bills: List[int]) -> bool:
        fives = tens = 0
        for bill in bills:
            if bill == 5:
                fives += 1
            elif bill == 10:
                if not fives:
                    return False
                fives -= 1
                tens += 1
            else:
                if tens and fives:
                    tens -= 1
                    fives -= 1
                elif fives >= 3:
                    fives -= 3
                else:
                    return False
        return True

摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个摆动序列，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为摆动序列的最长子序列的长度。

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        if len(nums) < 2:
            return len(nums)
        up = down = 1
        for i in range(1, len(nums)):
            if nums[i] > nums[i-1]:
                up = down + 1
            elif nums[i] < nums[i-1]:
                down = up + 1
        return max(up, down)

单调递增的数字

https://leetcode.cn/problems/monotone-increasing-digits/

当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

给定一个整数 n ，返回小于或等于 n 的最大数字，且数字呈单调递增。

class Solution:
    def monotoneIncreasingDigits(self, n: int) -> int:
        s = str(n)
        i = 1
        while i < len(s) and s[i - 1] <= s[i]:
            i += 1
        if i < len(s):
            while i > 0 and s[i - 1] > s[i]:
                s = s[:i - 1] + str(int(s[i - 1]) - 1) + '9' * (len(s) - i)
                i -= 1
        return int(s)