文章目录
一、 集成学习的三大关键领域 二、Bagging 方法的基本思想 三、RandomForestRegressor 的实现
在开始学习之前,先导入我们需要的库,并查看库的版本。 import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import seaborn as sns
import re, pip, conda
for package in [ sklearn, mlp, np, pd, sns, pip, conda] :
print ( re. findall( "([^']*)" , str ( package) ) [ 2 ] , package. __version__)
如果有缺少的库或者库的版本比较落后可以采用如下的代码进行下载更新。
pip install - - upgrade scikit- learn
conda update scikit- learn
集成学习(Ensemble learning)是机器学习中最先进、最有效、最具研究价值的领域之一,这类方法会训练多个弱评估器(base estimators)、并将它们输出的结果以某种方式结合起来解决一个问题。 在过去十年中,人工智能相关产业蓬勃发展,计算机视觉、自然语言处理、语音识别等领域不断推陈出新、硕果累累,但热闹是深度学习的,机器学习好似什么也没有。2012 年之后,传统机器学习占据的搜索、推荐、翻译、各类预测领域都被深度学习替代或入侵,在招聘岗位中,69% 的岗位明确要求深度学习技能,传统机器学习算法在这一场轰轰烈烈的人工智能热潮当中似乎有些被冷落了。 在人工智能大热的背后,集成学习就如同裂缝中的一道阳光,凭借其先进的思想、优异的性能杀出了一条血路,成为当代机器学习领域中最受学术界和产业界青睐的领域。 从今天的眼光来看,集成学习是: (1) 当代工业应用中,唯一能与深度学习算法分庭抗礼的算法; (2) 数据竞赛高分榜统治者,KDDcup、Kaggle、天池、DC 冠军队御用算法; (3) 在搜索、推荐、广告等众多领域,事实上的工业标准和基准模型; (4) 任何机器学习/深度学习工作者都必须掌握其原理、熟读其思想的领域。 在集成学习的发展历程中,集成的思想以及方法启发了众多深度学习和机器学习方面的工作,在学术界和工业界都取得了巨大的成功。今天,集成学习可以被分为三个主要研究领域: (2) 弱分类器集成。 弱分类器集成主要专注于对传统机器学习算法的集成,这个领域覆盖了大部分我们熟悉的集成算法和集成手段,如装袋法 bagging,提升法 boosting。这个领域试图设计强大的集成算法、来将多个弱学习器提升成为强学习器。 (3) 混合专家模型(mixture of experts)。 混合专家模型常常出现在深度学习(神经网络)的领域。在其他集成领域当中,不同的学习器是针对同一任务、甚至在同一数据上进行训练。 但在混合专家模型中,我们将一个复杂的任务拆解成几个相对简单且更小的子任务,然后针对不同的子任务训练个体学习器(专家),然后再结合这些个体学习器的结果得出最终的输出。 Bagging又称为装袋法,它是所有集成学习方法当中最为著名、最为简单、也最为有效的操作之一。 在 Bagging 集成当中,我们并行建立多个弱评估器(通常是决策树,也可以是其他非线性算法),并综合多个弱评估器的结果进行输出。 当集成算法目标是回归任务时,集成算法的输出结果是弱评估器输出的结果的平均值,当集成算法的目标是分类任务时,集成算法的输出结果是弱评估器输出的结果少数服从多数。 举例来说,假设现在一个 bagging 集成算法当中有 7 个弱评估器,对任意一个样本而言,输出的结果如下:
r_clf = np. array( [ 0 , 2 , 1 , 1 , 2 , 1 , 0 ] )
b_result_clf = np. argmax( np. bincount( r_clf) )
b_result_clf
bincount 会先将 array 由小到大进行排序,然后对每个数值进行计数,并返回计数结果的函数。需要注意的是,bincount 函数不能接受负数输入。 argmax 是找到 array 中最大值,并返回最大值索引的函数。 np. bincount( r_clf)
np. bincount( [ 3 , 0 , 2 , 1 , 1 , 2 , 1 , 0 ] )
np. argmax( np. array( [ 2 , 3 , 2 ] ) )
r_clf = np. array( [ 1 , 1 , 1 , - 1 , - 1 , - 1 , - 1 ] )
( r_clf == 1 ) . sum ( )
( r_clf == - 1 ) . sum ( )
b_result_clf = 1 if ( r_clf == 1 ) . sum ( ) > ( r_clf != 1 ) . sum ( ) else - 1
b_result_clf
r_clf = np. array( [ 1 , 1 , 1 , 0 , 0 , 0 , 2 , 2 ] )
从数量一致的类别中随机返回一个类别(需要进行随机设置)。 从数量一致的类别中,返回编码数字更小的类别(如果使用 argmax 函数)。
r_reg = np. array( [ - 2.082 , - 0.601 , - 1.686 , - 1.001 , - 2.037 , 0.1284 , 0.8500 ] )
b_result_reg = r_reg. mean( )
b_result_reg
在 sklearn 当中,我们可以接触到两个 Bagging 集成算法,一个是随机森林(RandomForest),另一个是极端随机树(ExtraTrees),他们都是以决策树为弱评估器的有监督算法,可以被用于分类、回归、排序等各种任务。 同时,我们还可以使用 bagging 的思路对其他算法进行集成,比如使用装袋法分类的类 BaggingClassifier 对支持向量机或逻辑回归进行集成。在课程当中,我们将重点介绍随机森林的原理与用法。 Bagging算法 集成类 随机森林分类 RandmForestClassifier 随机森林回归 RandomForestRegressor 极端随机树分类 ExtraTreesClassifier 极端随机树回归 ExtraTreesRegressor 装袋法分类 BaggingClassifier 装袋法回归 BaggingRegressor
随机森林是机器学习领域最常用的算法之一,其算法构筑过程非常简单:从提供的数据中随机抽样出不同的子集,用于建立多棵不同的决策树,并按照 Bagging 的规则对单棵决策树的结果进行集成(回归则平均,分类则少数服从多数)。 只要你充分掌握了决策树的各项属性和参数,随机森林的大部分内容都相当容易理解。 虽然原理上很简单,但随机森林的学习能力异常强大、算法复杂度高、又具备一定的抗过拟合能力,是从根本上来说比单棵决策树更优越的算法。 即便在深入了解机器学习的各种技巧之后,它依然是我们能够使用的最强大的算法之一。原理如此简单、还如此强大的算法在机器学习的世界中是不常见的。在机器学习竞赛当中,随机森林往往是我们在中小型数据上会尝试的第一个算法。 在 sklearn 中,随机森林可以实现回归也可以实现分类。随机森林回归器由类 sklearn.ensemble.RandomForestRegressor 实现,随机森林分类器则有类 sklearn.ensemble.RandomForestClassifier 实现。 我们可以像调用逻辑回归、决策树等其他 sklearn 中的算法一样,使用“实例化、fit、predict/score”三部曲来使用随机森林,同时我们也可以使用 sklearn 中的交叉验证方法来实现随机森林。其中回归森林的默认评估指标为 R2,分类森林的默认评估指标为准确率。 随机森林回归器实现模板如下: class sklearn . ensemble. RandomForestRegressor( n_estimators= 100 , * , criterion= 'squared_error' , max_depth= None , min_samples_split= 2 ,
min_samples_leaf= 1 , min_weight_fraction_leaf= 0.0 , max_features= 'auto' , max_leaf_nodes= None , min_impurity_decrease= 0.0 ,
bootstrap= True , oob_score= False , n_jobs= None , random_state= None , verbose= 0 , warm_start= False , ccp_alpha= 0.0 , max_samples= None )
class sklearn . ensemble. RandomForestClassifier( n_estimators= 100 , * , criterion= 'gini' , max_depth= None , min_samples_split= 2 ,
min_samples_leaf= 1 , min_weight_fraction_leaf= 0.0 , max_features= 'auto' , max_leaf_nodes= None , min_impurity_decrease= 0.0 ,
bootstrap= True , oob_score= False , n_jobs= None , random_state= None , verbose= 0 , warm_start= False , class_weight= None , ccp_alpha= 0.0 ,
max_samples= None )
不难发现,随机森林回归器和分类器的参数高度一致,因此我们只需要讲解其中一个类即可。任意集成算法在发源时都是回归类算法,因此我们的重点将会放在回归类算法上。 随机森林有大量的参数,幸运的是,随机森林中所有参数都有默认值,因此即便我们不学习任何参数,也可以调用随机森林算法。我们先来建一片森林看看吧: 先导入必要的库。 import matplotlib. pyplot as plt
from sklearn. ensemble import RandomForestRegressor as RFR
from sklearn. tree import DecisionTreeRegressor as DTR
from sklearn. model_selection import cross_validate, KFold
这里有几点需要注意: (1) 这里我们不再使用 cross_val_score,转而使用能够输出训练集分数的 cross_validate; (2) 决策树本身就是非常容易过拟合的算法,而集成模型的参数量/复杂度很难支持大规模网格搜索,因此对于随机森林来说,一定要关注算法的过拟合情况。 首先,我们先读入待操作的数据集,并通过 head() 函数读取其中的前五行数据。 data = pd. read_csv( r"D:\Pythonwork\2021ML\PART 2 Ensembles\datasets\House Price\train_encode.csv" , index_col= 0 )
data. head( )
可以通过 shape 函数得到数据的行列数量信息。 data. shape
X = data. iloc[ : , : - 1 ]
y = data. iloc[ : , - 1 ]
y
y. mean( )
X. shape
X. columns. tolist( )
reg_f = RFR( )
reg_t = DTR( )
cv = KFold( n_splits= 5 , shuffle= True , random_state= 1412 )
与 sklearn 中其他回归算法一样,随机森林的默认评估指标是 R2,但在机器学习竞赛、甚至实际使用时,我们很少使用损失以外的指标对回归类算法进行评估。对回归类算法而言,最常见的损失就是 MSE。 cross_validate 参数 n_jobs 允许该程序调用的线程数 verbose 是否打印进度
result_t = cross_validate( reg_t
, X, y
, cv= cv
, scoring= "neg_mean_squared_error"
, return_train_score= True
, verbose= True
, n_jobs= - 1
)
result_f = cross_validate( reg_f, X, y, cv= cv, scoring= "neg_mean_squared_error"
, return_train_score= True
, verbose= True
, n_jobs= - 1 )
result_t
result_f
在集成学习中,我们衡量回归类算法的指标一般是 RMSE(根均方误差),也就是 MSE 开根号后的结果。现实数据的标签往往数字巨大、数据量庞杂,MSE 作为平方结果会放大现实数据上的误差(例如随机森林结果中得到的,7∗108 等结果。 ,因此我们会对平房结果开根号,让回归类算法的评估指标在数值上不要过于夸张。同样的,方差作为平方结果,在现实数据上也会太大,因此如果可以,我们使用标准差进行模型稳定性的衡量。 trainRMSE_f = abs ( result_f[ "train_score" ] ) ** 0.5
testRMSE_f = abs ( result_f[ "test_score" ] ) ** 0.5
trainRMSE_t = abs ( result_t[ "train_score" ] ) ** 0.5
testRMSE_t = abs ( result_t[ "test_score" ] ) ** 0.5
trainRMSE_f. mean( )
testRMSE_f. mean( )
trainRMSE_f. std( )
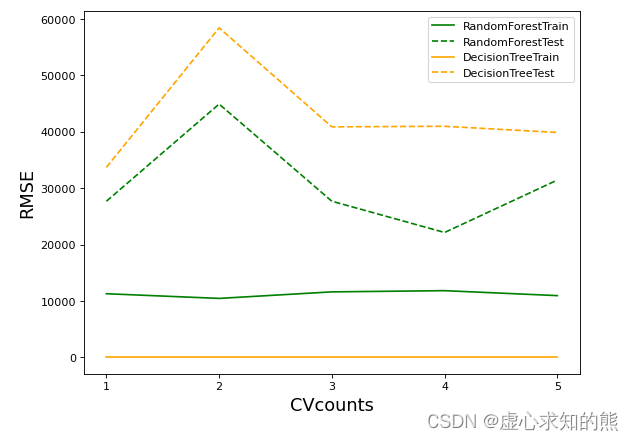
xaxis = range ( 1 , 6 )
plt. figure( figsize= ( 8 , 6 ) , dpi= 80 )
plt. plot( xaxis, trainRMSE_f, color= "green" , label = "RandomForestTrain" )
plt. plot( xaxis, testRMSE_f, color= "green" , linestyle= "--" , label = "RandomForestTest" )
plt. plot( xaxis, trainRMSE_t, color= "orange" , label = "DecisionTreeTrain" )
plt. plot( xaxis, testRMSE_t, color= "orange" , linestyle= "--" , label = "DecisionTreeTest" )
plt. xticks( [ 1 , 2 , 3 , 4 , 5 ] )
plt. xlabel( "CVcounts" , fontsize= 16 )
plt. ylabel( "RMSE" , fontsize= 16 )
plt. legend( )
plt. show( )
其中,横坐标表示交叉验证次数,纵坐标表示 RMSE 数值。 从图像来看,森林与决策树都处于过拟合状态,不过森林的过拟合程度较轻,决策树的过拟合程度较强。两个算法在训练集上的结果都比较优秀,决策树的可以完美学习训练集上的内容,达到 RMSE=0 的程度。 而随机森林在训练集上的 RMSE 大约在 1w 上下徘徊,测试集上的结果则是随机森林更占优。可见,与填写的参数无关,随机森林天生就是比决策树更不容易过拟合、泛化能力更强的。