数据结构很重要!
数据结构很重要!!
数据结构很重要!! !
思考
1.数据结构研究的内容有哪些?(What)
2.为什么要研究数据结构? ? (Why)
3.如何更好的研究数据结构? ? ?(How)
注:特别感谢青岛大学王卓老师
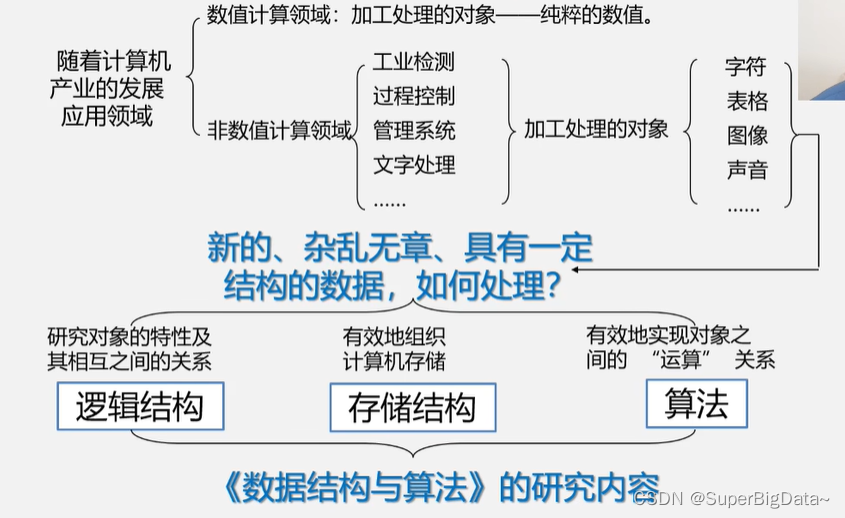
一.数据结构的研究

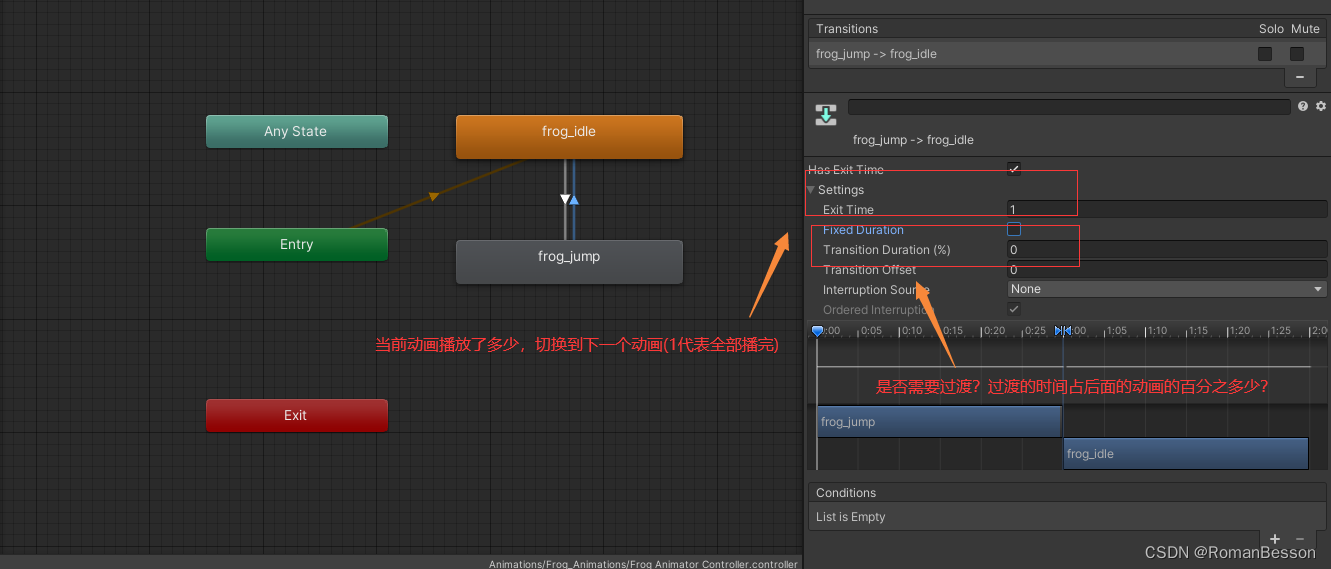
1.早期,计算机主要用于数值计算
例1.求解梁架结构中的应力。
1.抽象出数学模型:KU=M
2.提取操作对象:矩阵、向量
3.操作对象之间的关系(方程):一个矩阵一个未知的向量=一个向量
4.用数学语言表示:矩阵、向量,都用数组表示
解决:计算方法
特点:数据元素间关系简单,计算复杂
2.中期,计算机更多的用于非数值计算
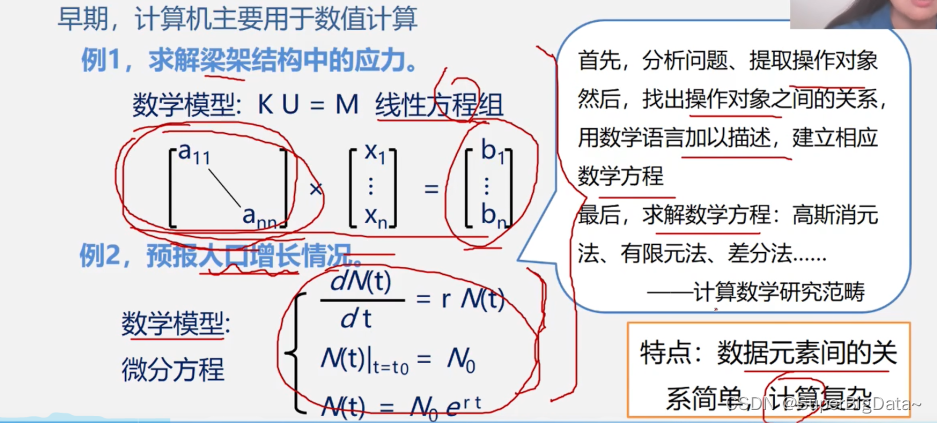
例1.学生学籍管理系统
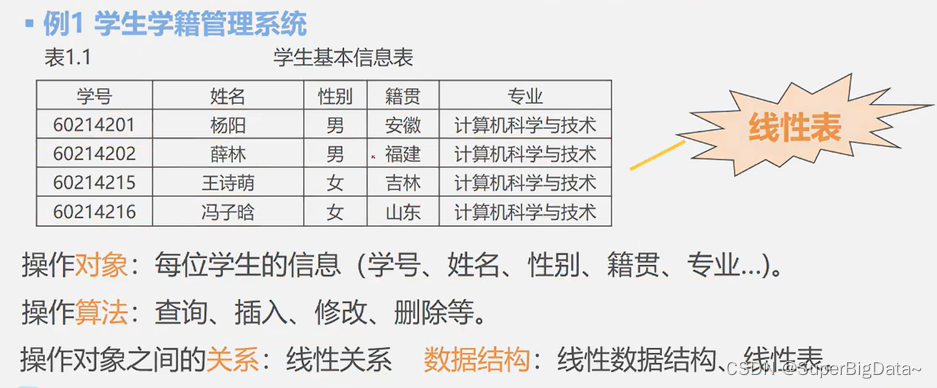
类似的还有图书管理系统、人事管理系统、仓库管理系统、通讯录
操作对象:若干行数据记录
操作算法:查询、增加、删除、修改等
操作对象之间的关系:线性关系
数据结构:线性数据结构,线性表
例2.人机对弈问题
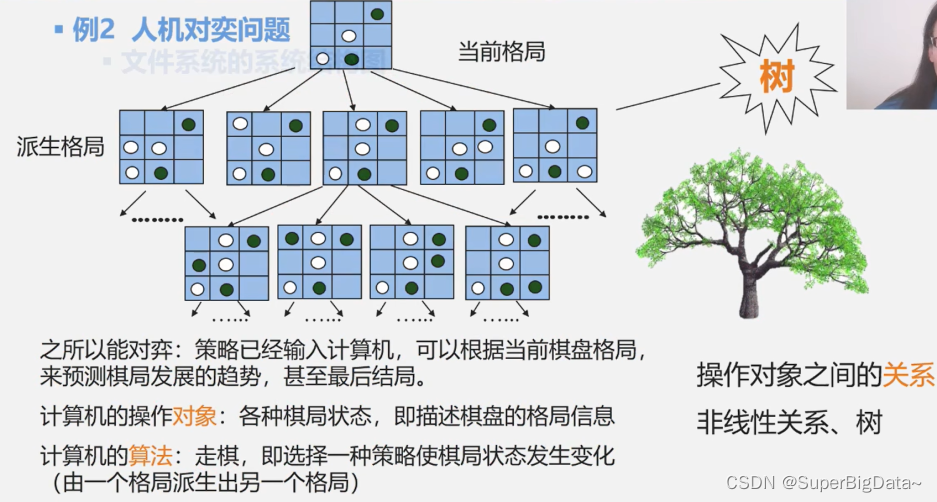
操作对象:棋局状态
操作算法:走棋,选择一种策略使棋局状态发生变化(一个格局派生出另一个格局)
操作对象之间的关系:树
数据结构:树
操作对象:目录
操作算法:查找目录
操作对象之间的关系:树
数据结构:树

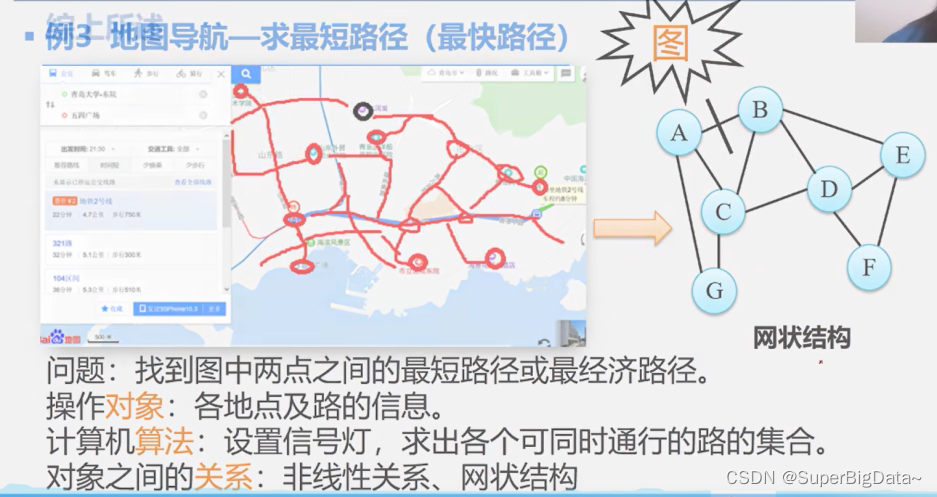
例3.地图导航-求最短路径
操作对象:各地点及路的信息
操作算法:设置信号灯,求出各个可同时通行的路的集合
操作对象之间的关系:非线性关系,网状结构
数据结构:图
3.综述
要想有效地使用计算机,就必须学习数据结构
背景:数值计算,大多用在公式或方程,已经满足不了需求了
解决:出现非数值计算方法,如表,树,图之类具有逻辑关系的数据。
数据结构:一门研究非数值计算的程序设计中计算机的操作对象,以及他们之间的关系和操作。
二.基本概念和术语
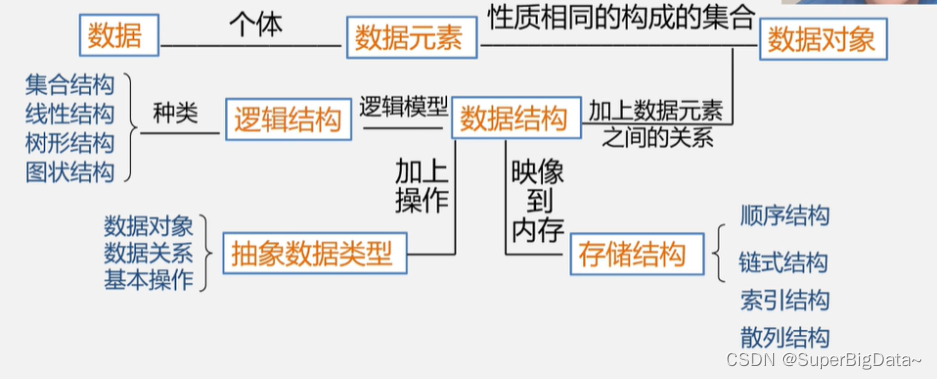
1.数据
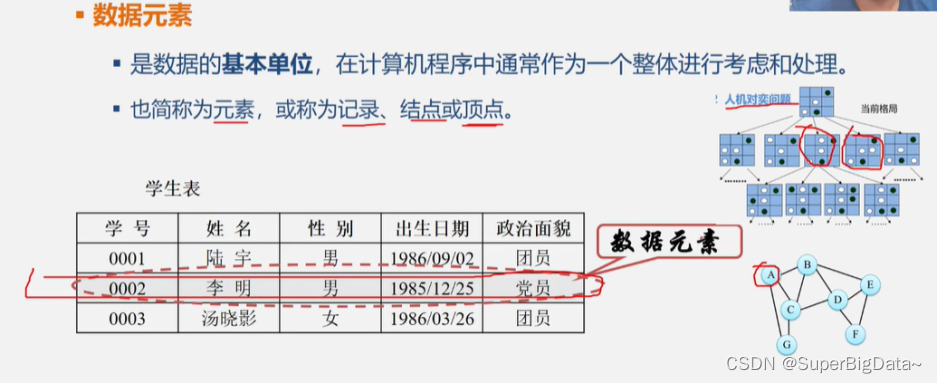
2.数据元素
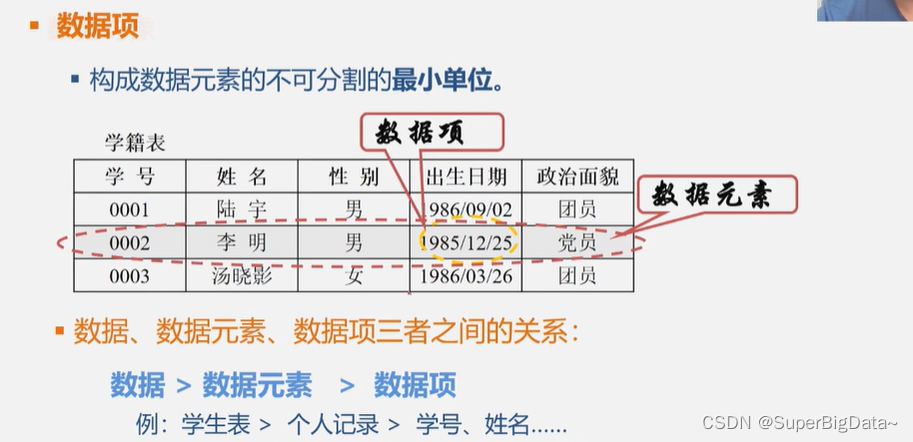
3.数据项
4.数据对象

5.数据元素与数据对象

6.数据结构


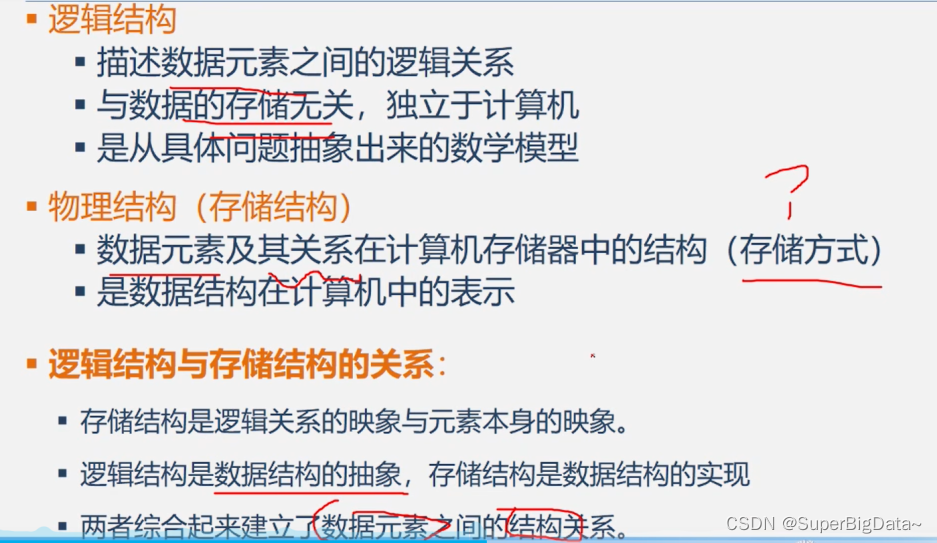
7.逻辑结构&存储结构
1.逻辑结构的种类
划分1:
划分2:
2.存储结构的种类

1.顺序存储结构

2.链接存储结构
一个存储存储单元:元素+下一个元素地址

3.索引存储结构
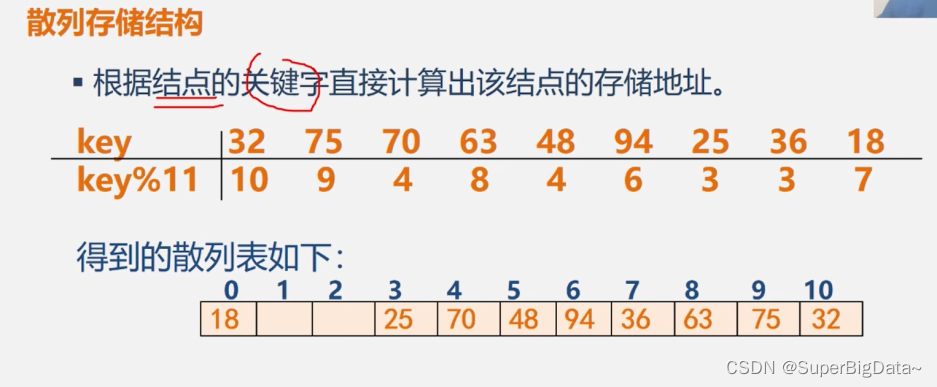
4.散列存储结构
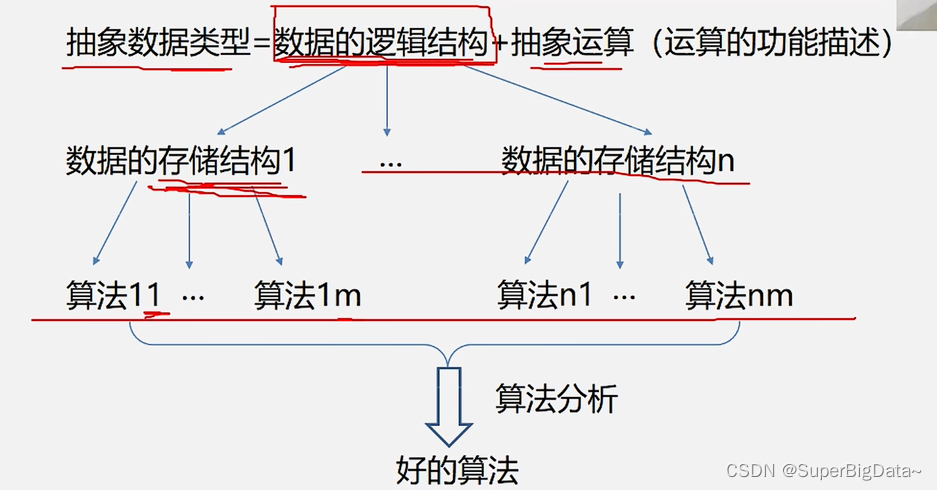
三.数据类型和抽象数据类型
1.基本数据类型



2.抽象数据类型(Abstract Data Type ,ADT)
抽象:从众多的事物中抽取出共同的、本质性的特征,而舍弃其非本质的特征的过程。反映事物的本质和规律的方法。
抽象数据类型:
1.从具体问题中抽象出来的一个数学模型,以及在数学模型上的一组操作。
2.不考虑计算机内的具体存储结构与运算的具体实现算法。
1.圆
舍弃:大小、颜色
圆的抽象定义:到每个点的距离相等的点的集合
运算:构造园、求面积、求周长

2.复数
抽象实质:实部+虚部i
操作:+、-、*、/

3.形式定义
具体问题—》抽象成数据类型
简洁严谨文字描述:形式定义

D是数据对象
S是数据对象上关系的集合,数据和数据关系很多,构成一个集合
P是对数据和数据关系操作的集合
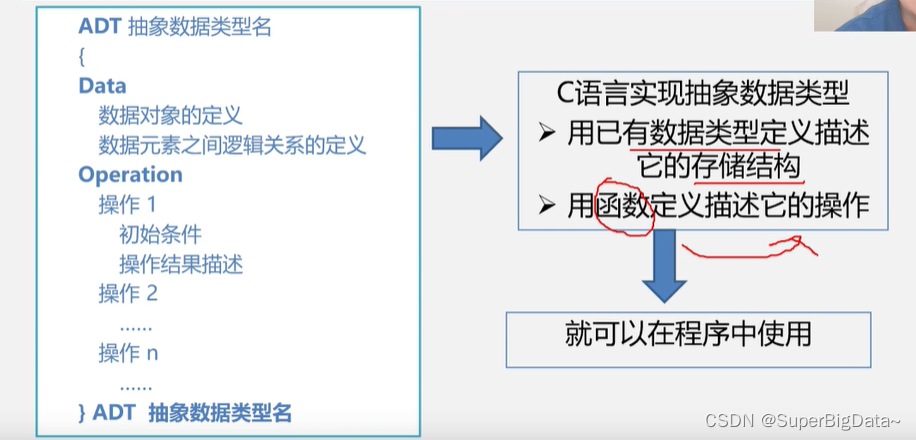
4.定义格式

操作结果:

5.定义举例
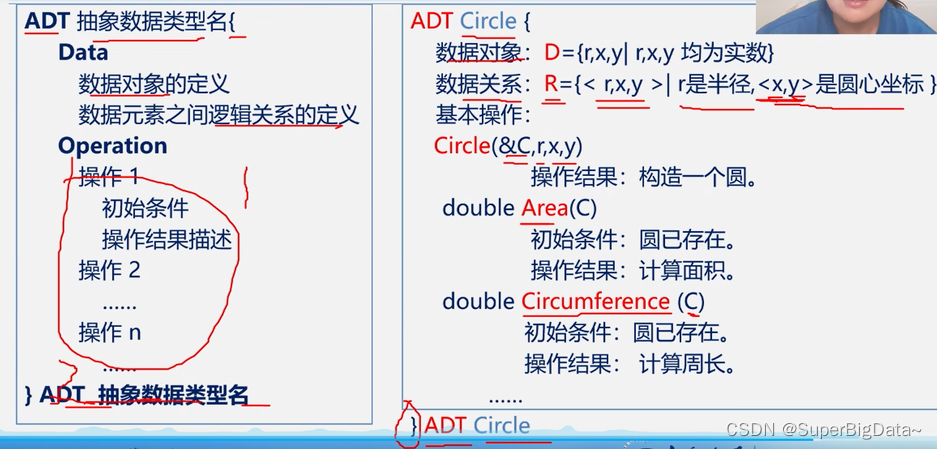
1.Circle的定义
2.复数的定义


3.总结
四.抽象数据类型的表示与实现
1.抽象数据类型
2.C语言实现抽象数据类型

3.抽象数据类型“复数”实现



五.算法和算法分析
1.算法的定义
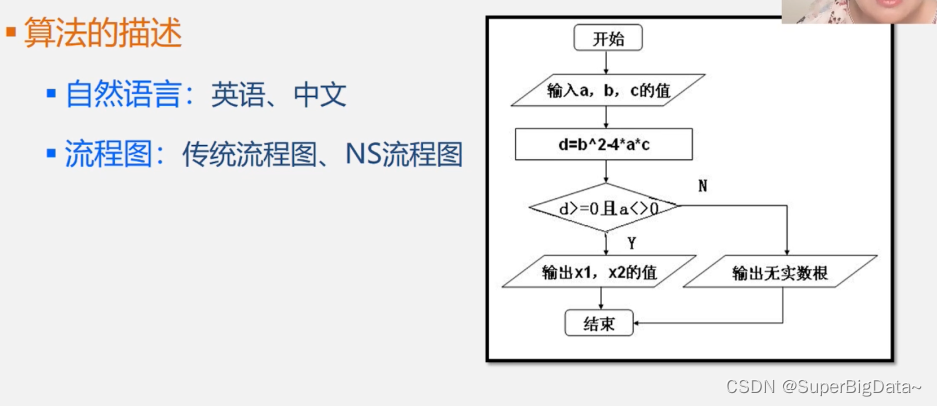
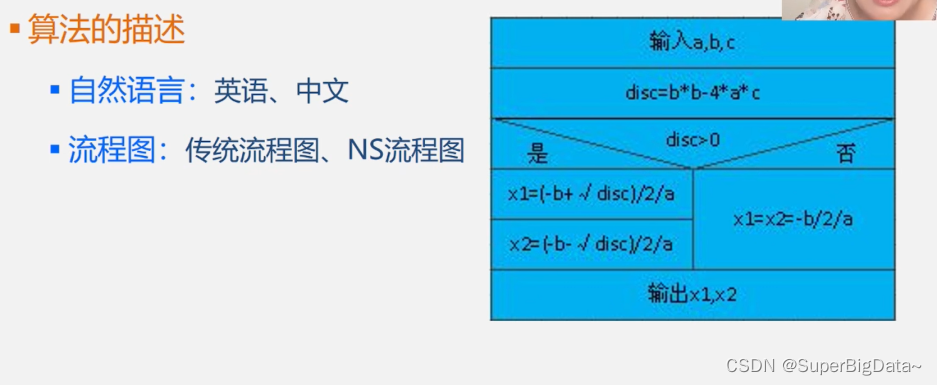
2.算法的描述


3.算法与程序

4.算法特性
1.有穷性:步骤、时间有穷,最后结束
2.确定性:算法中的每一条指令必须有确切的含义,没有二义性。多次执行输出结果一样。
3.可行性:操作可以通过已经实现的基本操作执行有限次来实现。
4.输入:一个算法有零个或多个输入。
5.输出:一个算法有一个或多个输出。
5.算法设计要求
1.正确性:算法满足问题要求,能正确解决问题

2.可读性:算法主要是为了人的阅读和交流,计算机只用来执行。

3.健壮性(鲁棒性):处理出错的方法,不应是中断程序的执行,而是返回一个表示错误或错误性质的值
4.高效性:要求花费尽量少的时间和尽量低的存储需求
6.算法和算法分析

所以,要根据问题实际需要,综合平衡有所侧重,结合计算机的性能,数据量大小。
1.算法时间效率度量

2.事前分析方法
算法运行时间=一种简单操作所需的时间*简单操作次数
也即算法中每条语句的执行时间之和
*算法运行时间=每条语句的执行次数(累加)该语句执行一次所需的时间

背景:每条语句执行一次所需的时间,一般是随机器而异的。取决于机器的指令性能、速度以及编译的代码质量。
由机器本身软硬件环境决定的,它与算法无关。
解决:所以,我们可以假设执行每条语句所需的时间均为单位时间。
结果:算法运行时间=每条语句频度之和。

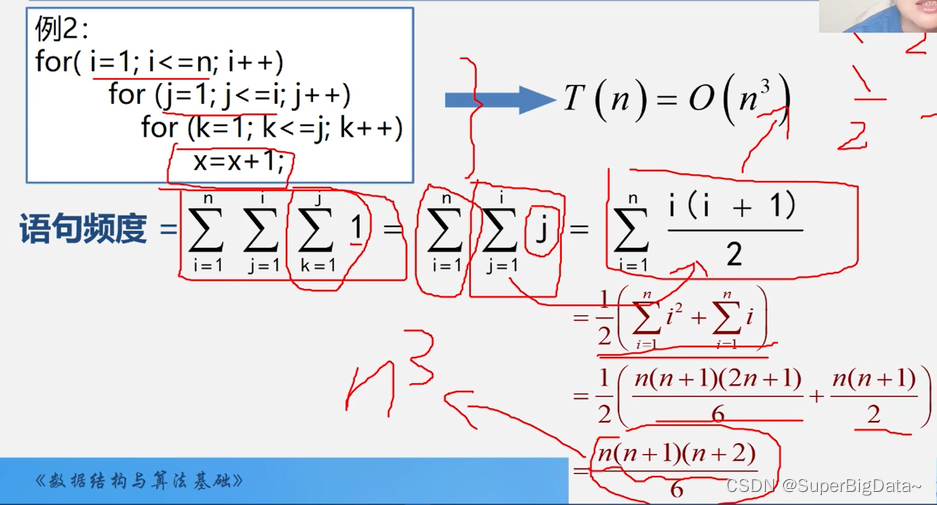
3.例子:俩个n*n矩阵相乘的算法可描述为

背景:便于比较,仅比较他们数量级,去除系数。
4.O(f(n)):算法渐进时间复杂度,简称时间复杂度

背景:一般情况下,不必计算所有操作的执行次数,只考虑算法中基本操作执行的次数(既然找数量级,只找贡献时间最大的语句)。

5.渐进时间复杂度意义
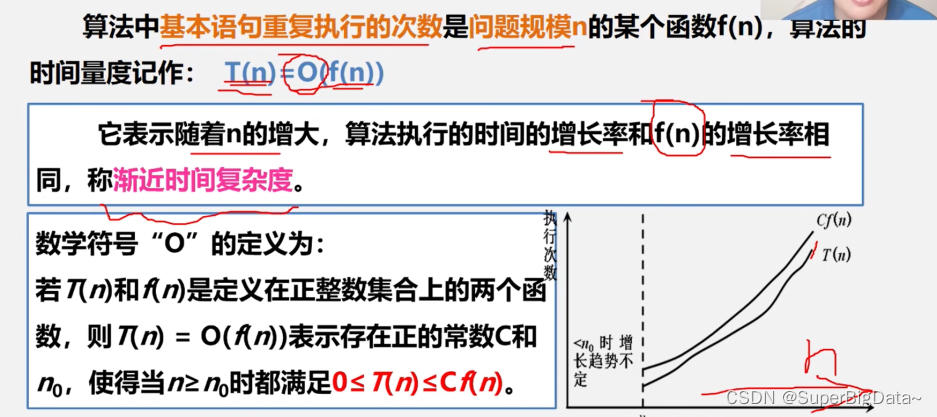
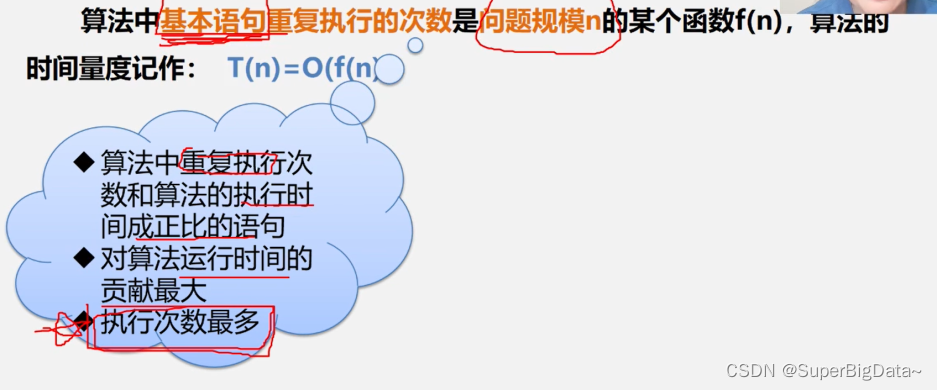
1.基本语句重复执行的次数:
● 算法中重复执行次数和算法的执行时间成正比语句
● 对算法运行时间贡献最大,执行次数最多
2.问题规模n:n越大算法的执行时间越长
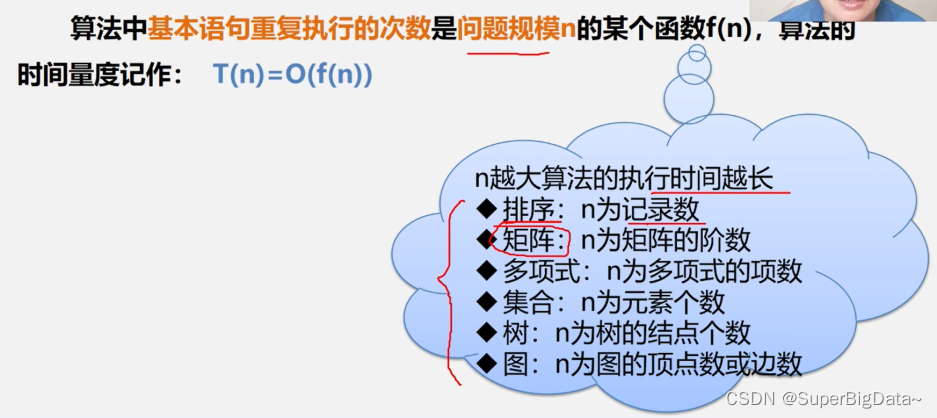
6.分析算法时间复杂度的基本方法
找最高次项,数量级最大的运算。

基本语句:语句频度最大的那条语句
1.找出嵌套最深的那条语句
2.求出f(n)多项式(核心的一步)
3.找出f(n)最大项级,然后等于O(f(n))

1.时间复杂度是由嵌套最深语句的频度决定的

2.例子1:N*N矩阵相乘

3.例子2:三层for循环
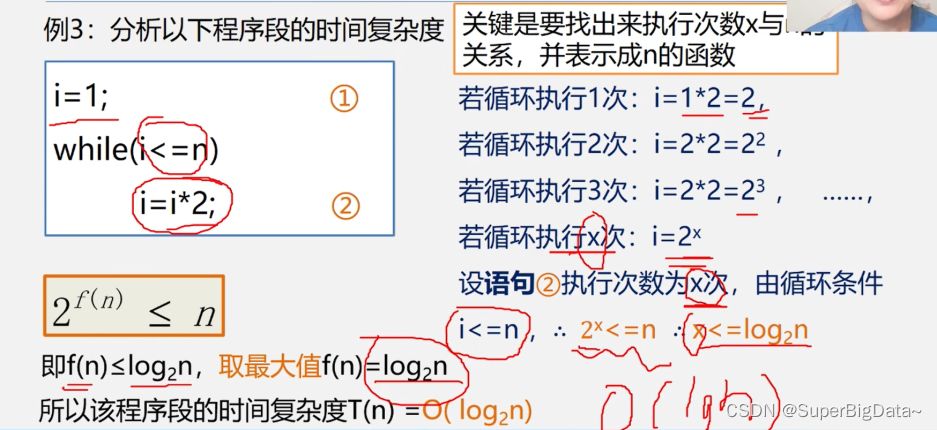
3.例子3:分析以下程序段的时间复杂度
关键:找出来执行次数X与N的关系,并表示成n的函数
7.算法时间复杂度计算
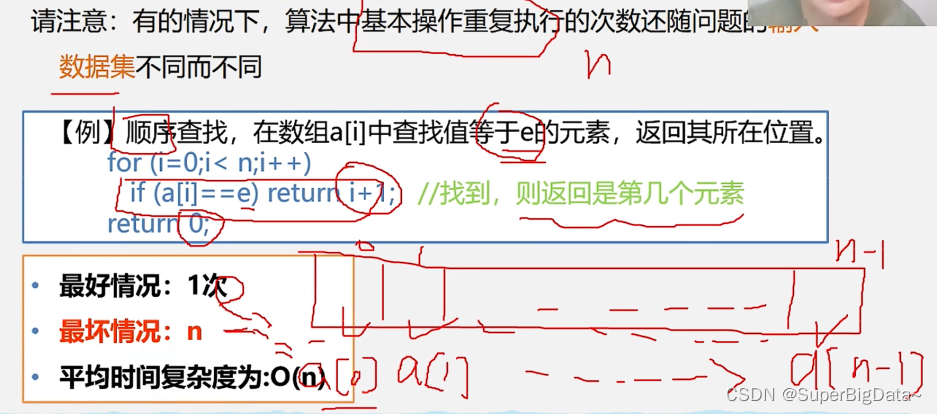
8.算法时间复杂度


9.算法时间效率的比较
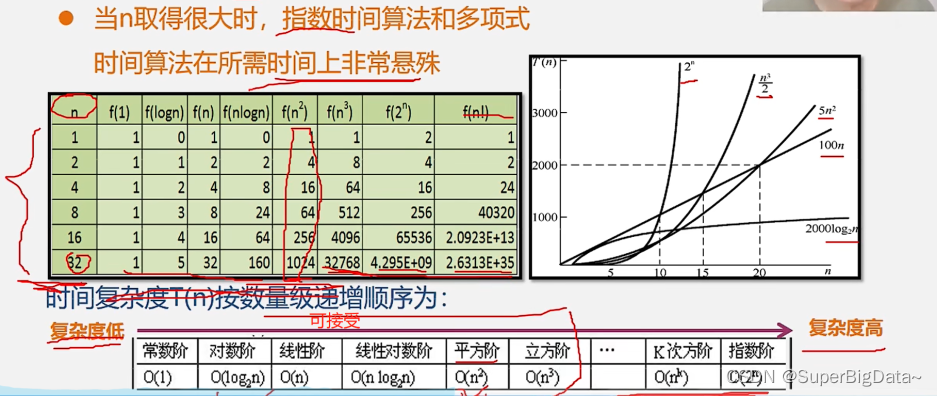
10.渐进空间复杂度

1.例子:一维数组逆序存放原数组

六.知识回顾

1.数据结构研究的内容有哪些?(What)
1.1基本概念和术语
1.数据结构
提取操作对象,找出操作对象之间的关系。
2.案例
学生学籍管理系统
对象:记录
关系:线性关系:
算法:增删查改
3.数据的定义
能输入计算机且能被计算机处理,的各种符号的集合。
数据是一种信息的载体,是对客观事物符号化的表示,能够被计算机识别、存储、加工。
分类:
1.数值型数据:整型、实数等
2.非数值数据:文字、图形、图像、声音等
4.数据元素
数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。
简称元素,或称为记录、节点、顶点。
5.数据项
构成数据元素不可分割的最小单位。
就是一张表中字段中的数据。
6.数据、数据元素、数据项之间的关系
数据项是数据元素集合的子集
数据元素是数据集合的子集
7.数据元素与数据对象
1.数据元素:组成数据的基本单位
○ 与数据的关系:是集合的个体
2.数据对象:性质相同的数据元素的集合
○ 与数据的关系是:集合的子集
8.数据结构内容
数据结构
a. 结构:数据元素不是孤立存在的,它们之间存在着某种关系,数据元素相互之间的关系称为结构
b. 相互之间存在一种或多种特定关系的数据元素集合
c. 数据结构是带结构的数据元素的集合
内容
a. 逻辑结构:数据之间存在逻辑关系
b. 物理结构:数据元素及其关系在计算机内存中的映像
c. 数据的运算与实现:对数据元素可以施加操作,以及这些操作相应存储在计算机内存当中。
9.逻辑结构&存储结构
1.逻辑结构
a. 描述数据元素之间的逻辑关系
b. 与数据的存储无关,独立于计算机
c. 是从具体问题抽象出来的数据模型
2.物理结构(存储结构)
数据元素及其关系在计算机存储器中的结构
3.逻辑结构与存储结构的关系
逻辑结构是数据结构的抽象,存储结构是数据结构的实现
二者综合起来建立了数据元素之间的结构关系
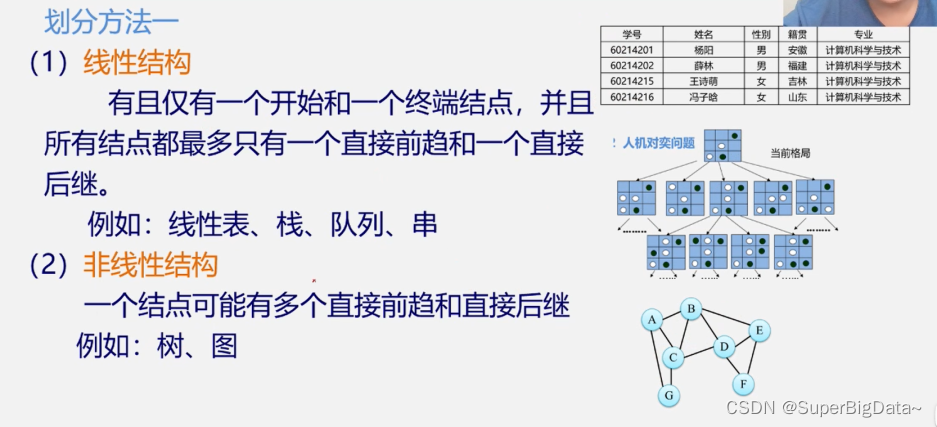
10.逻辑结构的种类
划分1:
(1)线性结构
有且只有一个开始和一个终端节点,并且所有结点都最多只有一个直接前驱和一个直接后继。
例如:线性表、栈、队列、串
(2)非线性结构
一个节点可能有多个直接前趋和直接后继
例如图
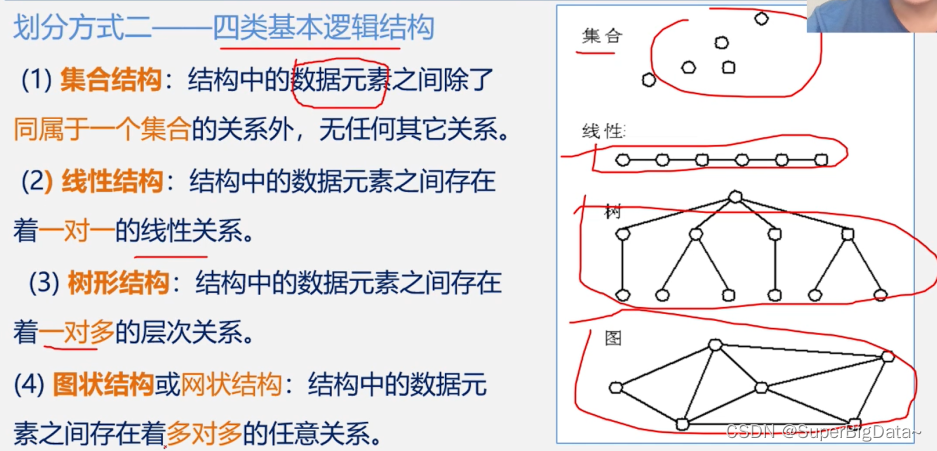
划分2:
(1)集合结构:同属于一个集合
(2)线性结构:元素之间存在一对一的线性关系
(3)树形结构:数据元素之间存在着一对多关系
(4)图、网状结构:数据元素存在多对多关系
11.存储结构的种类
- 顺序存储
一组连续的存储单元依此存储数据元素,数据之间的逻辑关系由存储位置来表示。
C语言中用数组来实现顺序存储结构。 - 链式存储
用一组任意的存储单元存储数据元素,数据元素之间的逻辑关系用指针来表示。
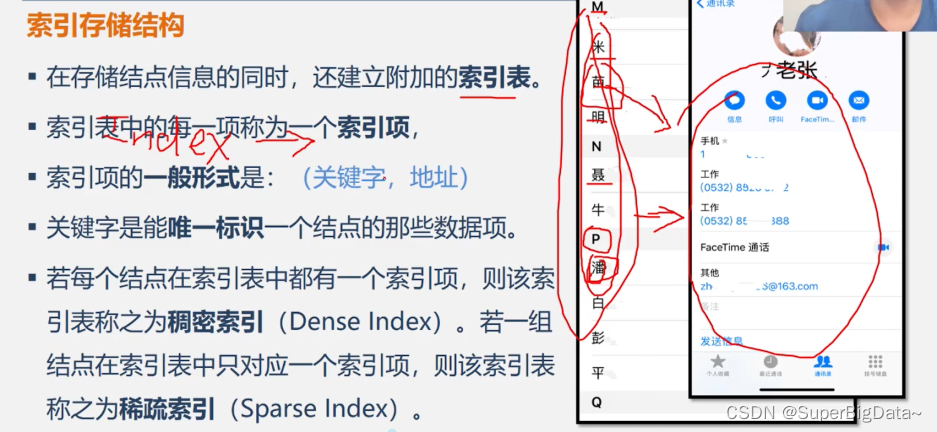
C语言中用指针来实现链式存储结构。 - 索引存储
存储结点信息的同时,还建立附加索引表。
索引项:关键字,地址,能唯一标识一个结点的那些数据项。
稠密索引:每个结点在索引表中都有一个索引项。
稀疏索引:一组结点在索引表中只对应一个索引项。 - 散列存储
根据结点的关键字直接计算出该结点的存储地址。
1.2基本数据类型和抽象类型
1.基本数据类型
数据类型:C语言中:
基本数据类型:int,char,float,double
构造数据类型:数组,结构体,枚举,共用体
指针、空(void)类型
用户也可以用typedef自己定义数据类型
基本的数据结构可以用数组,字符串。
数据类型的作用:
1.约束变量或常量的取值范围(int,char)
2.约束变量或常量的操作(+ - * /)
不能直接用数据类型表示的,还有另外一些数据结构:栈、队列、树、图。
数据类型:一组性质相同的值的集合,定义与这个值集合上的一组操作总称。
数据类型=值的集合+值集合上的一组操作。
2.抽象数据类型
抽象:反映事物的本质和规律的方法。
抽象数据类型:
1.从具体问题中抽象出一个数学模型,以及在数学模型上的一组操作
2.不考虑计算机内的具体存储结构与运算具体实现算法
例子:
舍弃:大小、颜色
圆的抽象定义:到每个点的距离相等的点的集合
运算:构造园、求面积、求周长
3.形式定义
具体问题—》抽象成数据类型
形式定义:简洁严谨文字描述
D是数据对象
S是数据对象上关系的集合,数据和数据关系很多,构成一个集合
P是对数据和数据关系操作的集合
4.定义格式
ADT 抽象数据类型名{
数据对象<数据对象的定义>
数据关系<数据关系的定义>
基本操作<基本操作的定义>
} ADT 抽象数据类型名
基本操作定义格式:
基本操作名(参数表:提供输入值,引用参数&打头,能将返回操作结果)
初始条件:(初始条件描述:若满足,执行下一步,反之)
操作结果:(操作结果描述:变化状况应返回)
5.定义举例
ADT 抽象数据名{
Data
数据对象的定义
数据元素之间逻辑关系的定义
Operation
操作1
初始条件
操作结果描述
操作2
初始条件
操作结果描述
}
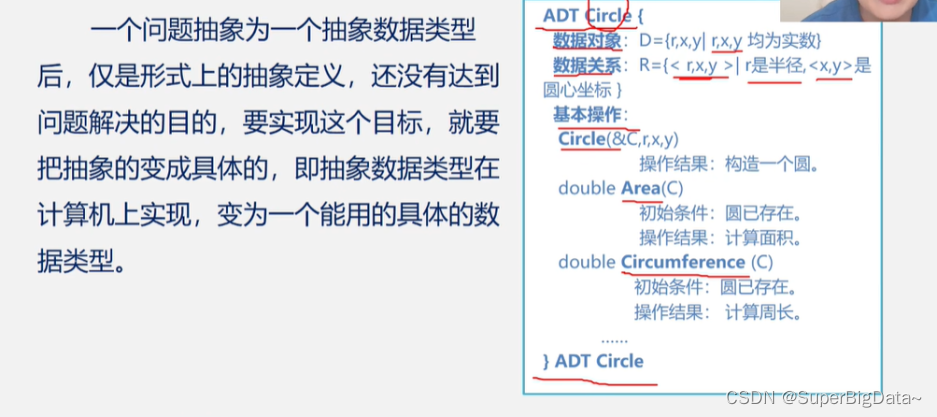
1.Circle的定义
ADT Circle{
数据对象:D={r,x,y|r,x,y均为实数}
数据关系:R={<r,x,y>|r是半径,<x,y>是圆心坐标}
基本操作:
Circle(&C,r,x,y)
操作结果:构造一个圆
double Area©
初始条件:圆已存在
操作结果:计算面积
}ADT Circle
2.复数的定义
ADT Complex{
数据对象:D={r1,r2|r1,r2都是实数}
数据关系:R={<r1,r2>|r1是实部,r2是虚部}
基本操作:
assign(&C,v1,v2)
初始条件:空的复数C已存在
操作结果:构造复数C,r1,r2分别被赋以v1,v2
destroy(&C)
初始条件:复数C以存在
操作结果:复数C被销毁
}ADT Circle
GetReal(Z,&realPart)
初始条件:复数以存在。操作结果:用realPart返回复数Z的实部值。
GetReal(Z,&ImagPart)
初始条件:复数以存在。操作结果:用ImagPart返回复数Z的虚部值。
Add(Z1,Z2,&sum)
初始条件:Z1,Z2都是复数。操作结果:sum返回俩个复数Z1,Z2的和。
6.总结
1.3抽象数据类型的表示与实现
1.抽象数据类型
一个问题抽象为一个抽象数据类型
2.C语言实现抽象数据类型
用已有数据类型、函数定义表示操作
3.抽象数据类型“复数”实现
typedef struct{
float realpart;
float imagpart;
}Complex
void assign(Complex *A,float real,float imag);
void add(Complex *C,Complex A,Complex B);
void assign(Complex *A,float real,float imag){
A->realpart=real;
A->imagpart=imag;
}
void add(Complex *C,Complex A,Complex B){
C->realpart=A.realpart+B.realpart;
C->imagpart=A.imagpart+A.imagpart;
}
#include<stdio.h>
int main(){
Complex z1,z2,z3,z4,z;
float realpart,imagpart;
assign(z1,8.0,7.5); //构造复数z1
assign(z2,6.0,9.5); //构造复数z2
add(z3,z1,z2); //俩个复数相加
multiply(z4,z1,z2); //俩个复数相乘
if(divide(z,z1,z2)){
GetReal(z,realpart);
GetImag(z,imagpart);
}
return 0;
}
1.4算法和算法分析
1.算法的定义
对特定问题求解方法和步骤的一种描述,它是有限的指令序列。
每一个指令表示一个或多个操做。
2.算法的描述
自然语言:英文、中文
流程图:传统流程图、NS流程图
伪代码:类C语言
程序代码:C,Java语言
3.算法与程序
算法:解决问题的一种方法或一个过程,考虑如何将输入转换成输出,一个问题可以有多种算法。
程序:用某种程序设计语言对算法的具体实现
程序=数据结构+算法
数据结构通过算法来实现操作
算法根据数据结构设计程序
4.算法特性
- 有穷性:步骤、时间有穷,最后结束
- 确定性:没有二义性,每次输入一样的,最后都能得到一样的结果
- 可行性:可以实现的操作
- 输入:可以有0个或多个输入
- 输出:有一个或多个输出
5.算法设计要求
- 正确性:满足程序要求,能正确解决问题
- 可读性:算法主要是为了人的阅读和交流,其次才是为了计算机执行,因此算法应该易于人的理解
- 健壮性:进行错误处理,而不是直接终端程序的执行
- 高效性:要求花费尽量少的时间和尽量低的存储需求
6.算法和算法分析
正确性->健壮性->可读性->算法的效率
算法的效率:
1.时间效率:算法执行过程中所耗费的时间
2.空间效率:算法执行过程中所耗费的存储空间
注:要根据实际问题需求,综合平衡,有所侧重,结合计算机的性能,数据量大小。
2.为什么要研究数据结构? ? (Why)
2.1为什么研究数据结构?
1.时间推移
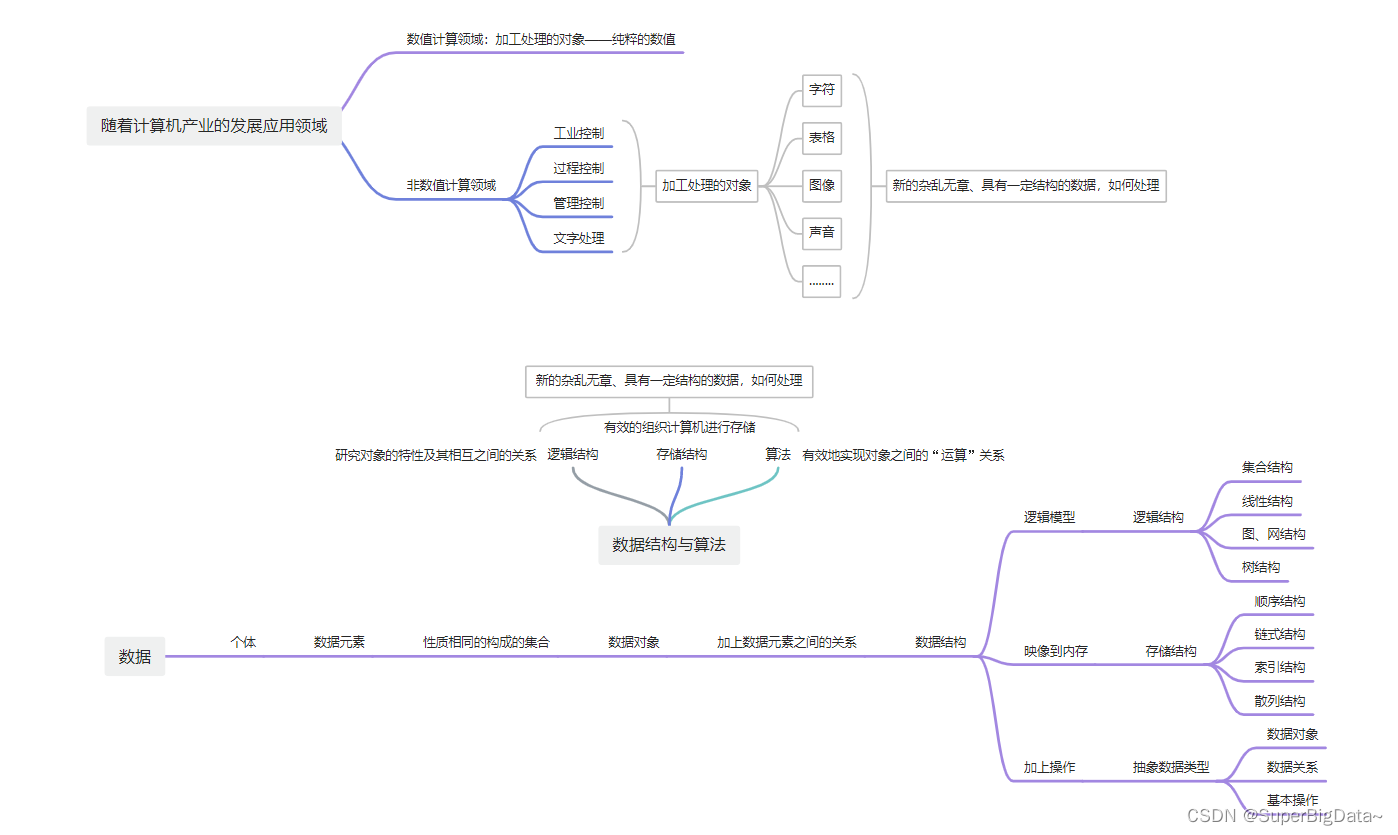
随着计算机产业的发展应用领域,数值计算领域已经不能满足了(纯粹的数值计算)
非数值计算领域的需求量大增,产生了很多新的、杂乱无章的数据、具有一定结构的数据需要处理。比如(声音、图片、视频、字符…)
开始处理这些杂乱无章的数据:
逻辑结构:数据元素对象及其之间的关系
存储结构:数据对象及关系映射存储到计算机中
算法:实现数据对象之间的“运算”关系。
2.传统数据类型数据范围和操作有一定限制
如果数据类型表示的不合适,那么可以选择另外一些数据结构:栈、队列、树、图。
2.2为什么要研究基本概念和术语?
只有清晰知道基本概念,才能更好的学习数据结构
基本概念:
- 数据
- 数据元素
- 数据项
- 数据对象
- 数据元素和数据对象
- 数据结构
- 逻辑结构&存储结构
数据类型:
- 基本数据类型
- 抽象数据类型
算法:
- 算法的定义
- 算法的描述
- 算法与程序
- 算法特性
- 算法设计要求
3.如何更好的研究数据结构? ? ?(How)
搞清楚,基本的数据定义,扎实基础。
用心
用心、用心
用心、用心、用心
知其然、知其所以然!!!
多学习,多思考,多总结,多输出,多交流 (five kills)~~~



![[算法]归并排序](https://img-blog.csdnimg.cn/78bc8bdfcbce425b9e129e47ca3fb8dc.png)