1.分割回文串

题目链接

思路：回溯算法的组合方法（分割问题类似组合问题）。

流程图：红色竖杠就是startIndex。 for循环是横向走，递归是纵向走。

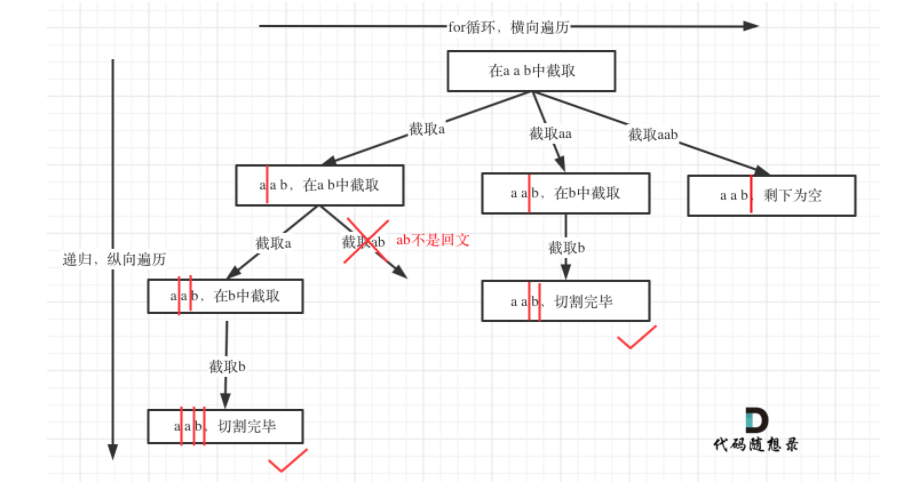
回溯三部曲：

• 递归函数参数：字符串s和startIndex，因为是在同一个集合中进行分割或组合，就需要startIndex

• 递归函数终止条件：只要切割线切到了字符串最后面，就终止，然后add到result数组中（这里默认已经判断回文了）

• 单层搜索的逻辑：在for (int i = startIndex; i < s.size(); i++)循环中，我们定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。

解法：

class Solution {
    List<List<String>> res = new ArrayList<>();
    LinkedList<String> path = new LinkedList<>();
    public List<List<String>> partition(String s) {
        back(s, 0);
        return res;
    }

    // 递归函数参数
    private void back(String s, int startIndex) {
        // 终止条件
        if (startIndex >= s.length()){
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < s.length(); i++){
            // 如果是回文子串就path.add
            if (isPalindrome(s, startIndex, i)){
                path.add(s.substring(startIndex, i + 1));
            }else
                continue;
            back(s, i + 1);
            path.removeLast();  // 回溯
        }
    }

    // 判断是否为回文子串
    private boolean isPalindrome(String s, int startIndex, int end) {
        for (int i = startIndex, j = end; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}

2.子集

题目链接

思路：这个题是典型的组合问题。

• 子集是收集树形结构中树的所有节点的结果。

• 而组合问题、分割问题是收集树形结构中叶子节点的结果

注意：for循环里，每次都要i<nums.length。

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> subsets(int[] nums) {
        back(nums, 0);
        return res;
    }

    private void back(int[] nums, int startIndex) {
        res.add(new ArrayList<>(path));
        for (int i = startIndex; i < nums.length; i++){
            path.add(nums[i]);
            back(nums, i + 1);
            path.removeLast();
        }
    }
}