2017年第七届MathorCup高校数学建模挑战赛
A题 流程工业的智能制造
原题再现:
“中国制造 2025”是我国制造业升级的国家大战略。其技术核心是智能制造,智能化程度相当于“德国工业 4.0”水平。“中国制造 2025”的重点领域既包含重大装备的制造业,也包含新能源、新材料制造的流程工业。
在流程工业中,钢铁冶金,石油化工等行业是代表性的国民经济支柱性产业。其生产过程的系统优化与智能控制的目标函数包括节能,优质,低耗,绿色环保等多目标要求。为了实现这样的优化目标,生产过程智能控制的关键技术就要从原来的反馈控制进一步升级为预测控制。即通过生产工艺大数据的信息物理系统(Cyber Physical System)建模,通过大数据挖掘,确定生产过程的最佳途径与最佳参数控制范围,预测性地动态调整生产过程控制,获得最佳生产效果。
以高炉冶炼优质铁水为例,高炉炼铁过程是按加料顺序由高炉顶部加入矿石和焦炭等原燃料,由高炉下部连续鼓入热风、喷入煤粉进行炉温调整的冶炼过程。从原燃料炉顶加入,到冶炼成炉渣和铁水,其冶炼周期 6-8 小时。而高炉每经过2 小时就出渣、出铁一次。并且化验得到此次出铁的铁水与炉渣的化学成分。因此,前后两炉铁水含硅量,即炉温之间是具有相关性的。炼铁过程是一个离散加入,连续冶炼,离散输出的复杂生产过程。
炼铁过程的机理既包含由热平衡/物料平衡约束的化学反应过程,也包括由三相流体动力学混合的物理运动过程。因此完整的冶炼过程机理模型是一个由代数方程组和偏微分方程组构成的复杂数学模型,模型方程如下:
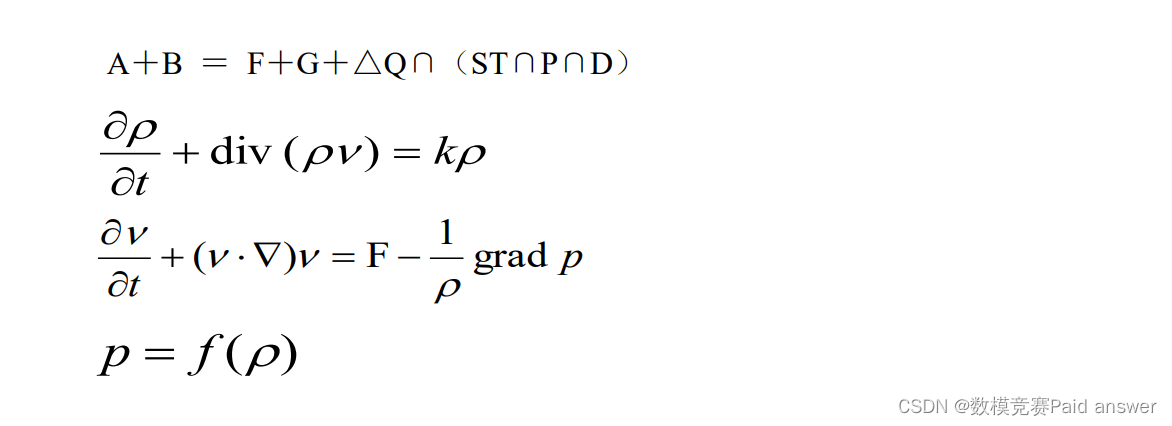
从机理上求解上述混合动力学方程组的最优解是尚未解决的数学难题。因此,通过大数据的数据挖掘技术对其进行过程优化是一条可行的求解途径。
炼铁过程依时间顺序采集的工艺参数是一个高维的大数据时间序列。影响因素数以百计。其终极生产指标产量、能耗、铁水质量等指标都与冶炼过程的一项控制性中间指标——炉温,即铁水含硅量[Si](铁水含硅质量百分数)密切相关。对 2 小时后或 4 小时后高炉炉温上升或下降的预测,即[Si]时间序列的预测关系着当前高炉各项操作参数的调控方向。因此,[Si]的准确预测控制建模成为冶炼过程优化与预测控制的关键技术。
为了简化问题,本项目仅提供由铁水含硅量[Si]、含硫量[S]、喷煤量 PML和鼓风量 FL 组成的数据库作为数学建模分析和数据挖掘的基础。序号 N 既是数据序列的序号,其实也是高炉出铁时间的顺序序号。
本课题数学建模的要求是:
(1)从给定数据表中[Si]-[S]-FL-PML 依序号排列的 1000 炉生产大数据中,自主选取学习样本和算法,建立[Si]预测动态数学模型,包括一步预测模型和二步预测模型。全面论述你的数学建模思路。
(2)自主选取验证样本,验证你所建立的数学模型的预测成功率。包括数值预测成功率和炉温升降方向预测成功率。并且讨论其动态预测控制的可行性。
(3)以质量指标铁水含硫量[S]为例,含硫量低,铁水质量好,可以生产优质钢,制造优质装备。试建立质量指标[S]的优化数学模型,并且讨论按照优化模型计算结果进行[Si]预测控制的预期效果。
(4)讨论你所建立的复杂流程工业智能控制大数据建模的心得体会。

整体求解过程概述(摘要)
在我国制造业升级“中国制造 2025”的国家战略下,为了预测控制高炉炼铁过程,本文建立了神经网络预测模型、混沌时间序列预测模型,并基于遗传算法(GA)改进了神经网络模型,使用粒子群算法(PSO)优化了含硫量[S]。
针对问题一,首先,本文对附件所给数据进行了数据预处理,剔除了异常值并归一化,得到 932 组有效数据。然后,建立 BP 神经网络预测模型预测了含硅量[Si],并分析了含硅量[Si]、含硫量[S]、鼓风量 FL 和喷煤量 PML 之间的相关性。其次,建立了小波神经网络预测模型和遗传算法(GA)优化的 BP 神经网络预测模型,并比较了三者优劣。接着,选取训练样本数据 922 组,验证样本数据 10 组,发现遗传算法优化的 BP 神经网络预测模型和小波神经网络预测模型预测效果较好,BP 神经网络预测模型较差。最后,本文建立了混沌时间序列预测模型,并对含硅量[Si]进行了混沌局部线性一步预测和二步预测。
针对问题二,首先,本文选取了 922 组数据作为训练样本,10 组数据作为验证样本,将传统的 BP 神经网络预测模型、小波神经网络模型预测模型、基于遗传算法优化 BP 神经网络预测模型和混沌时间序列预测模型,分别预测后 10炉次含硅量[Si]的结果与实际值进行对比,计算得到:BP 预测成功率为 20%,小波预测为 70%,GA+BP 预测为 60%,混沌预测为 80%。其次,通过不同的模型分别预测了后 10 炉次含硅量[Si]的结果,预测了炉温升降方向,计算得到:BP预测成功率为 40%,小波预测为 100%,GA+BP 预测为 100%,混沌预测为 100%。最后,通过讨论神经网络训练函数的选取、神经网络性能参数的设定与混沌时间
序列预测邻域半径的选取,分析了动态预测控制的可行性。
针对问题三,首先,本文根据遗传算法(GA)优化 BP 神经网络的预测模型,预测了含硫量[S],并找出了含硫量[S]与含硅量[Si]、鼓风量 FL 和喷煤量 PML之间的关系。然后,本文使用粒子群算法(PSO)优化了含硫量[S],得出当鼓风量归一化后 FL=0.7012 和喷煤量 PML=0.0809 时,含硫量[S]有最小值。最后,本文分析了在含硫量[S]最优条件下,预测控制含硅量[Si]的预期效果,在含硫量[S]取最小值时,预测到此时含硅量[Si]较小,为 0.5712。
针对问题四,我们结合建模背景、求解模型所得结果与分析结果所得结论,根据复杂流程工业智能控制的意义,浅谈了建模的心得体会。通过大数据挖掘,我们可以确定生产过程的最佳途径与最佳参数范围,获得最佳生产效果。
模型假设:
(1)假设在混沌局部线性预测中,邻域ε的选取客观准确,主观性较小。
(2)假设在混沌局部线性预测中,局部特性可以准确代表整体特性。
(3)假设在神经网络预测中,输入变量作为网络的第一层合理有效。
(4)假设附件中提供的数据及所使用的数据都真实准确。
(5)假设铁水含硅量[Si]、含硫量[S]、喷煤量 PML 和鼓风量 FL 组成的数据能代表高炉炼铁过程,体现高炉炼铁特性。
问题分析:
问题一的分析:在问题一中,题目要求我们从给定数据表中[Si]-[S]-FL-PML依序号排列的 1000 炉生产大数据中,自主选取学习样本和算法,建立[Si]预测动态数学模型,包括一步预测模型和二步预测模型。其中的一步预测模型和二步预测模型指的是预测步长分别取 1 和 2,前后两炉铁水含硅量,即炉温之间是具有相关性的。这里的学习样本不能是全部的 1000 炉生产大数据,因为问题二中需要我们验证所建立的数学模型的预测成功率,所以不能选择全部数据来训练,只能选择一部分数据来学习训练。至于建模的算法,需要结合问题本身来选择。
问题二的分析:在问题二中,题目要求我们自主选取验证样本,验证我们所建立的数学模型的预测成功率,包括数值预测成功率和炉温升降方向预测成功率。并且讨论其动态预测控制的可行性。我们需要从 1000 炉生产大数据中剩下未学习训练的数据中,选取验证样本,验证包括[Si]含量和炉温升降方向的成功率。难点在于讨论其动态预测控制的可行性,以及如何提高算法的预测成功率。
问题三的分析:在问题三中,题目要求我们以质量指标铁水含硫量[S]为例,含硫量低,铁水质量好,可以生产优质钢,制造优质装备。试建立质量指标[S]的优化数学模型,并且讨论按照优化模型计算结果进行[Si]预测控制的预期效果。通过大数据挖掘,确定生产过程的最佳途径与最佳参数控制范围,预测性地动态调整生产过程控制,获得最佳生产效果,建立优化模型,讨论对[Si]的预测控制。
问题四的分析:在问题四中,题目要求我们讨论我们所建立的复杂流程工业智能控制大数据建模的心得体会,这需要结合我们模型的结果和背景来讨论。
模型的建立与求解整体论文缩略图



全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
The actual procedure is shown in the screenshot
1 def BP(sampleinnorm, sampleoutnorm,hiddenunitnum=3):
2 # 超参数
3 maxepochs = 60000 # 最大迭代次数
4 learnrate = 0.030 # 学习率
5 errorfinal = 0.65*10**(-3) # 最终迭代误差
6 indim = 3 # 输入特征维度3
7 outdim = 2 # 输出特征唯独2
8 # 隐藏层默认为3个节点,1层
9 n,m = shape(sampleinnorm)
10 w1 = 0.5*np.random.rand(hiddenunitnum,indim)-0.1 #8*3维
11 b1 = 0.5*np.random.rand(hiddenunitnum,1)-0.1 #8*1维
12 w2 = 0.5*np.random.rand(outdim,hiddenunitnum)-0.1 #2*8维
13 b2 = 0.5*np.random.rand(outdim,1)-0.1 #2*1维
14
15 errhistory = []
16
17 for i in range(maxepochs):
18 # 激活隐藏输出层
19 hiddenout = sigmod((np.dot(w1,sampleinnorm).transpose()+b1.transpose())).transpose()
20 # 计算输出层输出
21 networkout = (np.dot(w2,hiddenout).transpose()+b2.transpose()).transpose()
22 # 计算误差
23 err = sampleoutnorm - networkout
24 # 计算代价函数(cost function)sum对数组里面的所有数据求和,变为一个实数
25 sse = sum(sum(err**2))/m
26 errhistory.append(sse)
27 if sse < errorfinal: #迭代误差
28 break
29 # 计算delta
30 delta2 = err
31 delta1 = np.dot(w2.transpose(),delta2)*hiddenout*(1-hiddenout)
32 # 计算偏置
33 dw2 = np.dot(delta2,hiddenout.transpose())
34 db2 = 1 / 20 * np.sum(delta2, axis=1, keepdims=True)
35
36 dw1 = np.dot(delta1,sampleinnorm.transpose())
37 db1 = 1/20*np.sum(delta1,axis=1,keepdims=True)
38
39 # 更新权值
40 w2 += learnrate*dw2
41 b2 += learnrate*db2
42 w1 += learnrate*dw1
43 b1 += learnrate*db1
44
45 return errhistory,b1,b2,w1,w2,maxepochs
import numpy as np
#定义激活函数
def sigmoid(x,deriv=False):
if deriv == True:
return x*(1-x)
return 1/(1+np.exp(-x))
x = np.array([[0,0,0],[0,1,1],[1,0,1],[0,0,1],[0,0,1]])
print(x.shape)
#指定label值
y = np.array([[0],[1],[1],[0],[0]])
print(y.shape)
#指定随机化种子,使得每次随机值一样
np.random.seed(1)
#定义三层的神经网络
w0 = 2*np.random.random((3,4)) - 1
w1 = 2*np.random.random((4,1)) - 1
print(w0)
print(w1)
for j in range(6000):
l0 = x
l1 = sigmoid(np.dot(l0,w0))
l2 = sigmoid(np.dot(l1,w1))
#真实值-预测值
l2_error = y - l2
if j%1000 == 0 :
print("error"+str(np.mean(np.abs(l2_error))))
l2_delta = l2_error*sigmoid(l2,deriv=True)
l1_error = l2_delta.dot(w1.T)
l1_delta = l1_error*sigmoid(l1,deriv=True)
#更新w0 w1
w1 += l1.T.dot(l2_delta)
w0 += l0.T.dot(l1_delta)