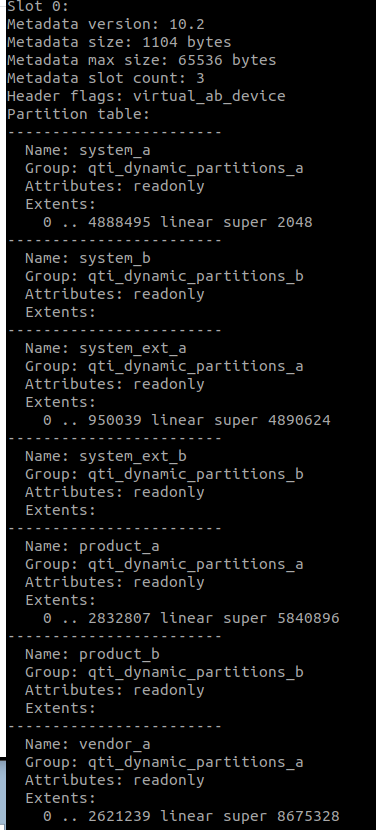
文章目录
- 基本概念
- 概念1
- 概念2:Kernel Func
- 总结
- 内积矩阵(Gram/Kernel Matrix)
- 一些思考
- 什么是有限正半定
- 常用的Kernel Functions
- Linear Kernel
- Polynomial Kernel
- RBF(Gaussian) Kernel
基本概念
概念1
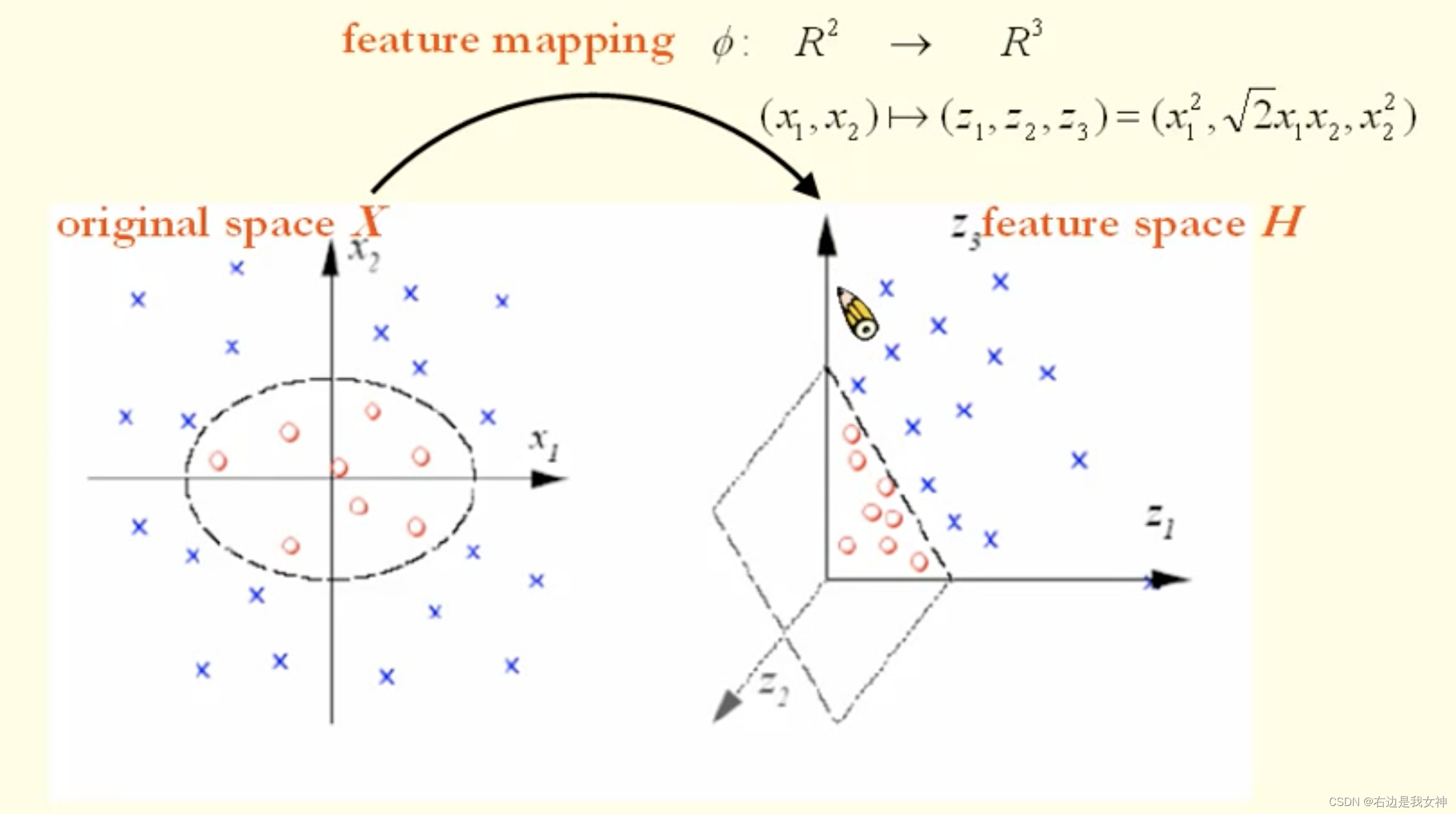
高维空间存在可分的情况。
我们可以找一个映射函数送过去。
概念2:Kernel Func
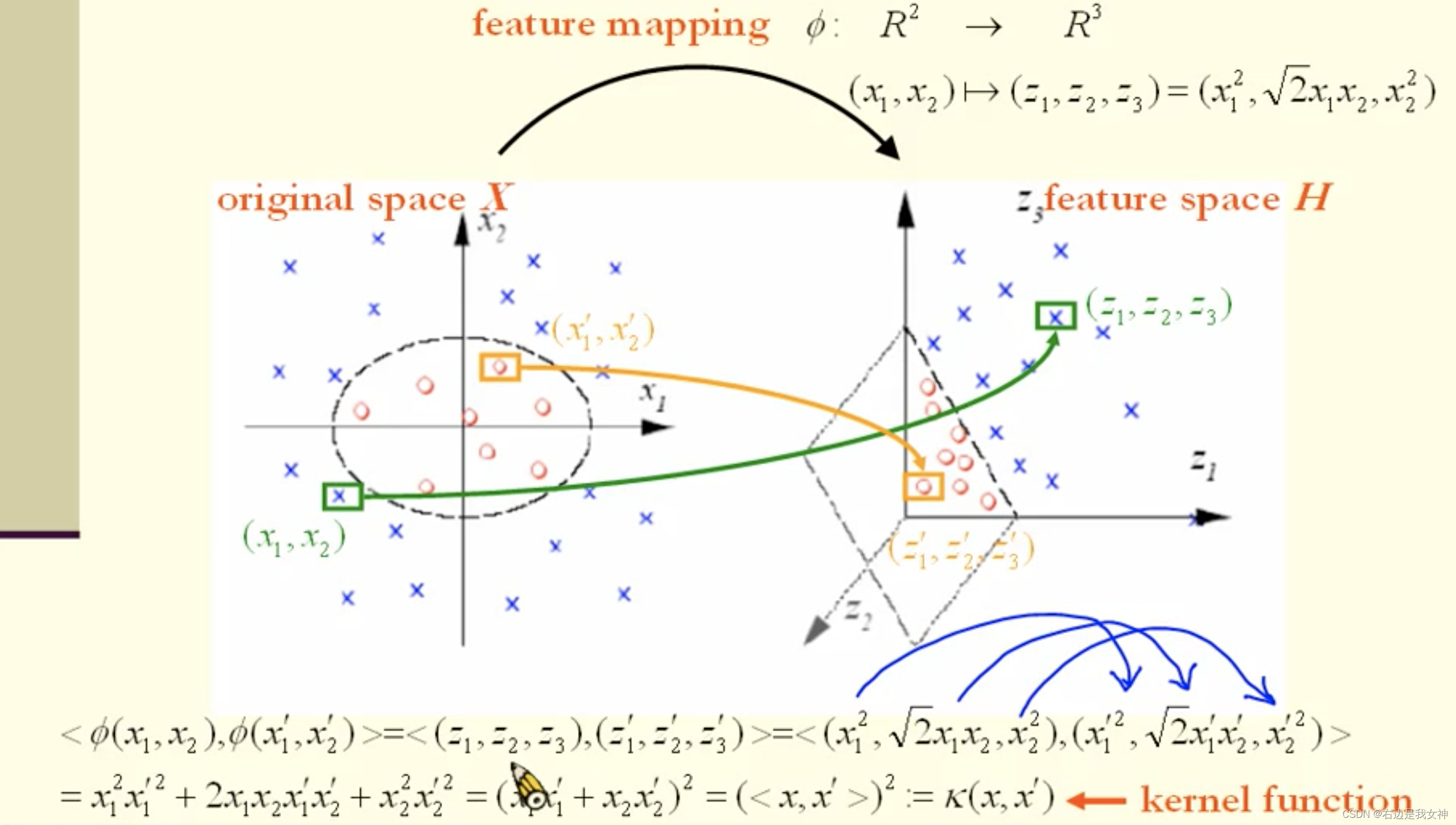
高维空间的内积可以通过低维空间的内积表示。
这样的表示方法即为核函数。
也就是说,只要知道核函数,就知道高维空间的内积。
总结
Kernel Methods起作用,通过:
- 把数据送到另一个空间(通常具有高的维度);
- 在新的空间找到一个线性关系(可以将数据分开)。
如果映射选择合适,复杂的关系能够被简化。
另外,我们观察得到:
- 映射空间的几何性质可以通过内积来表示;
- 内积的计算是简单的。

内积矩阵(Gram/Kernel Matrix)
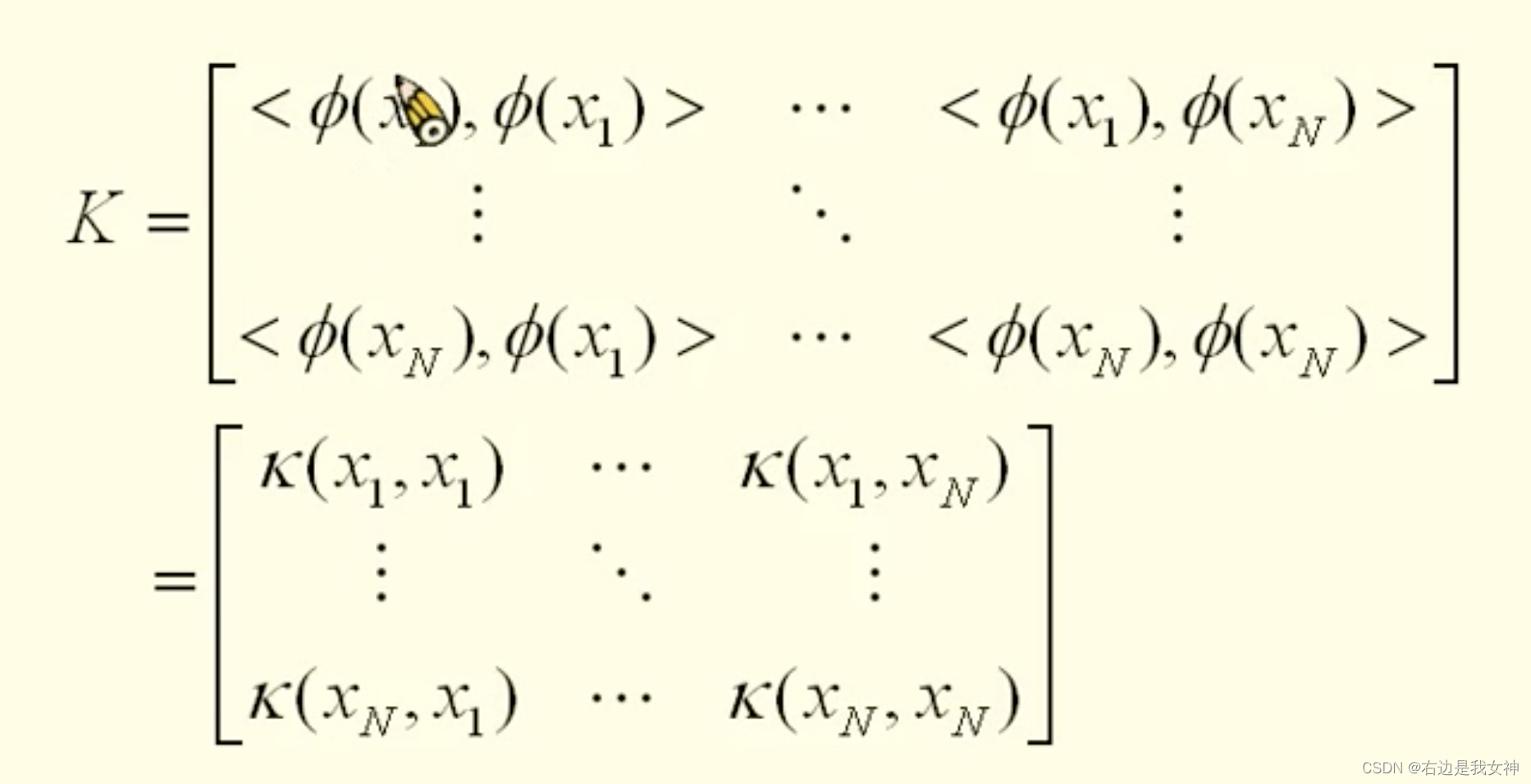
一些思考
- 映射函数是否必要?(不一定需要。)
- 是不是只用核函数即可?(是的。)
- 什么样的核函数能被使用?(满足有限正半定。)
- 给一个映射,是否一定能找到一个核函数?(是的。)
- 给一个核函数,是否一定能构建一个特征空间/映射?(是的。)
什么是有限正半定
一个函数:
k
:
X
×
X
→
R
k:X\times X\to R
k:X×X→R
满足有限正半定当且仅当对于有限个样本
x
x
x,它的内积矩阵是一个正半定矩阵。
另外,思考4和5对应定理:Characterization of Kernels。
常用的Kernel Functions
Linear Kernel
K ( x , z ) = x ⋅ z K(x,z)=x\cdot z K(x,z)=x⋅z
什么时候用:特征比较丰富,样本数据量大,需要进行实时得出结果的问题。
优点:简单,不需要设置任何参数,可以直接使用。
Polynomial Kernel
K
(
x
,
z
)
=
(
γ
x
⋅
z
+
ζ
)
p
,
γ
>
0
K(x,z)=(\gamma x\cdot z+\zeta)^p,\gamma\gt0
K(x,z)=(γx⋅z+ζ)p,γ>0
γ
\gamma
γ对内积进行放缩、
ζ
\zeta
ζ控制常数项、
q
q
q控制高次项。
维度和阶没有必然关系,只是特征空间核原空间的映射关系的体现。
RBF(Gaussian) Kernel
K ( x , z ) = exp ( − ∥ x − z ∥ 2 2 σ 2 ) K(x,z)=\exp(-\frac{\|x-z\|^2}{2\sigma^2}) K(x,z)=exp(−2σ2∥x−z∥2)
表示什么:两个样本点之间相似的程度(欧氏距离)。

上述式子在凑两个样本点的内积表示。
高斯核函数可以表示为无穷维度的特征。
其他样本点和当前样本点的高斯核函数结果作为当前样本点的特征。
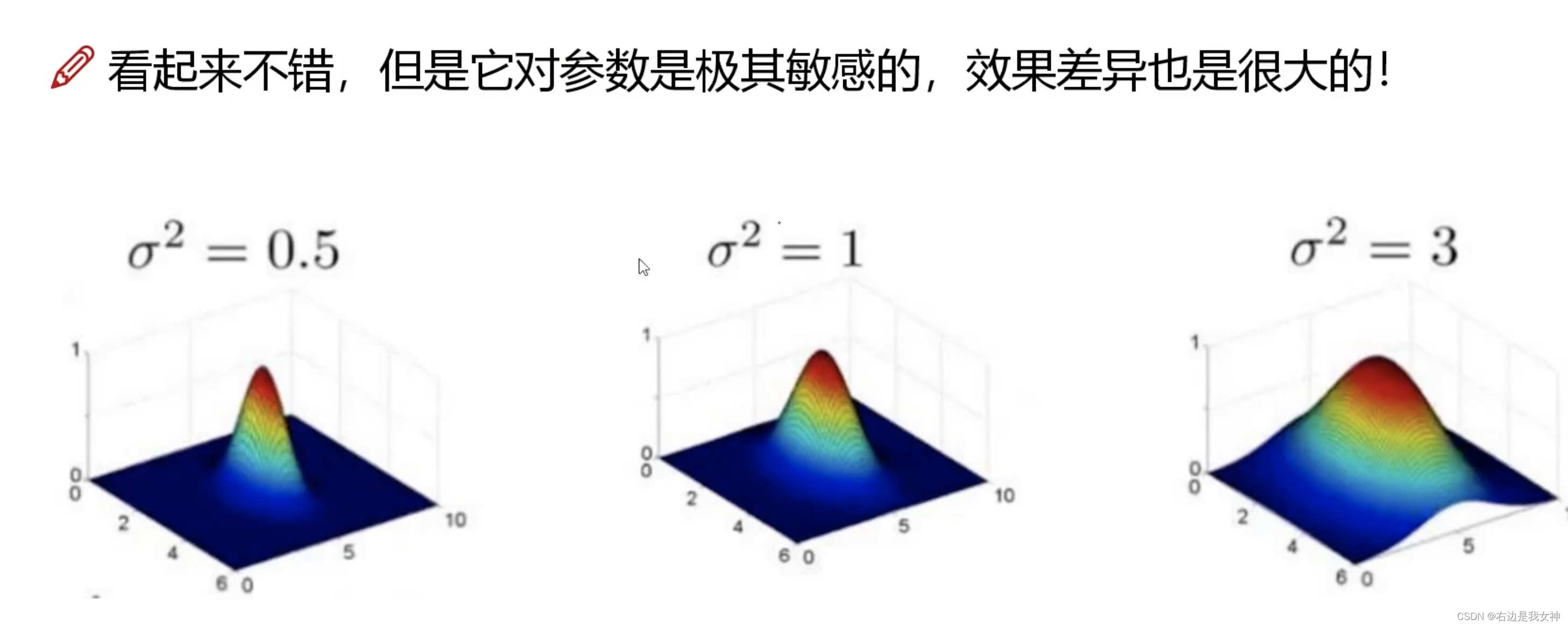
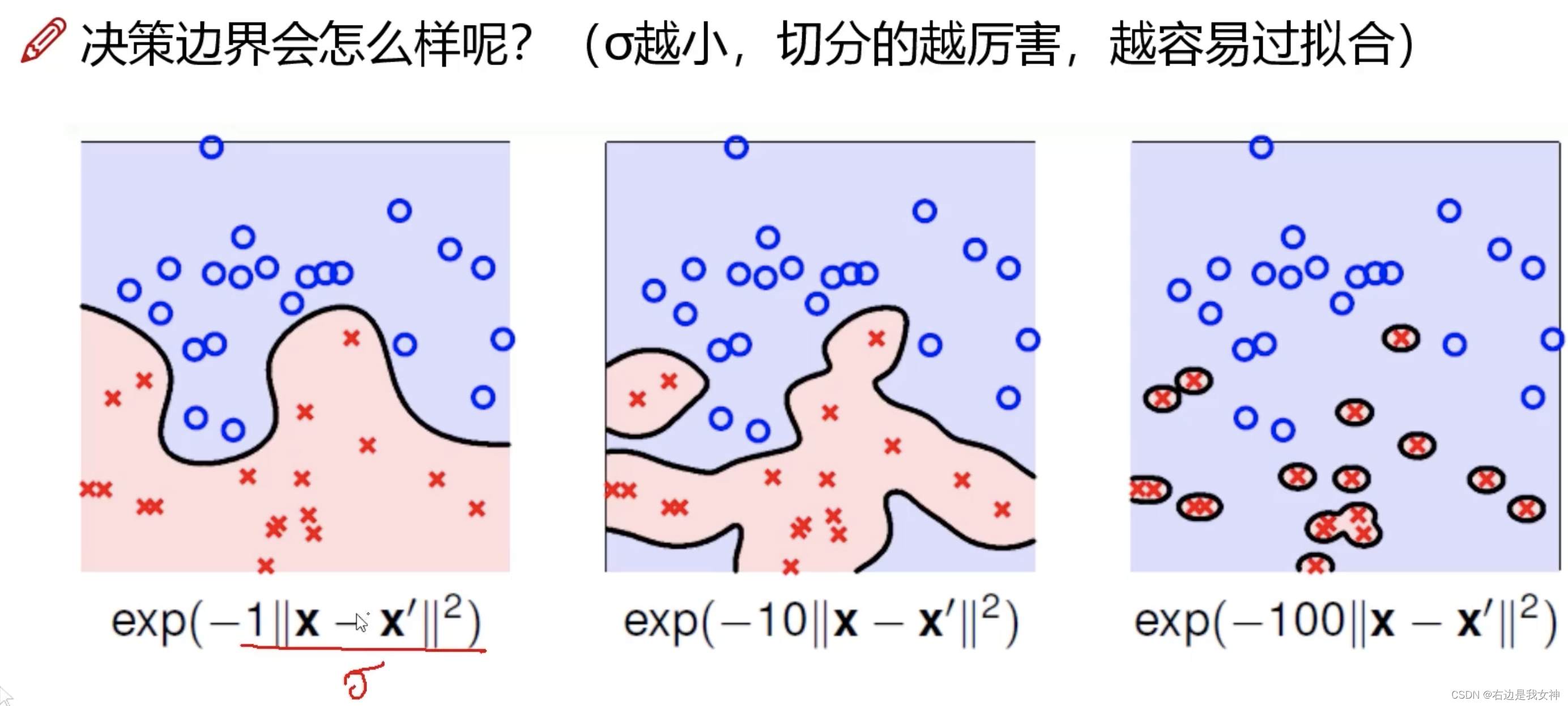
就是说:







![[go学习笔记.第十七章.redis的使用] 1.redis的使用](https://img-blog.csdnimg.cn/3c1b1bd5127849738cfb6f846160e71b.png)