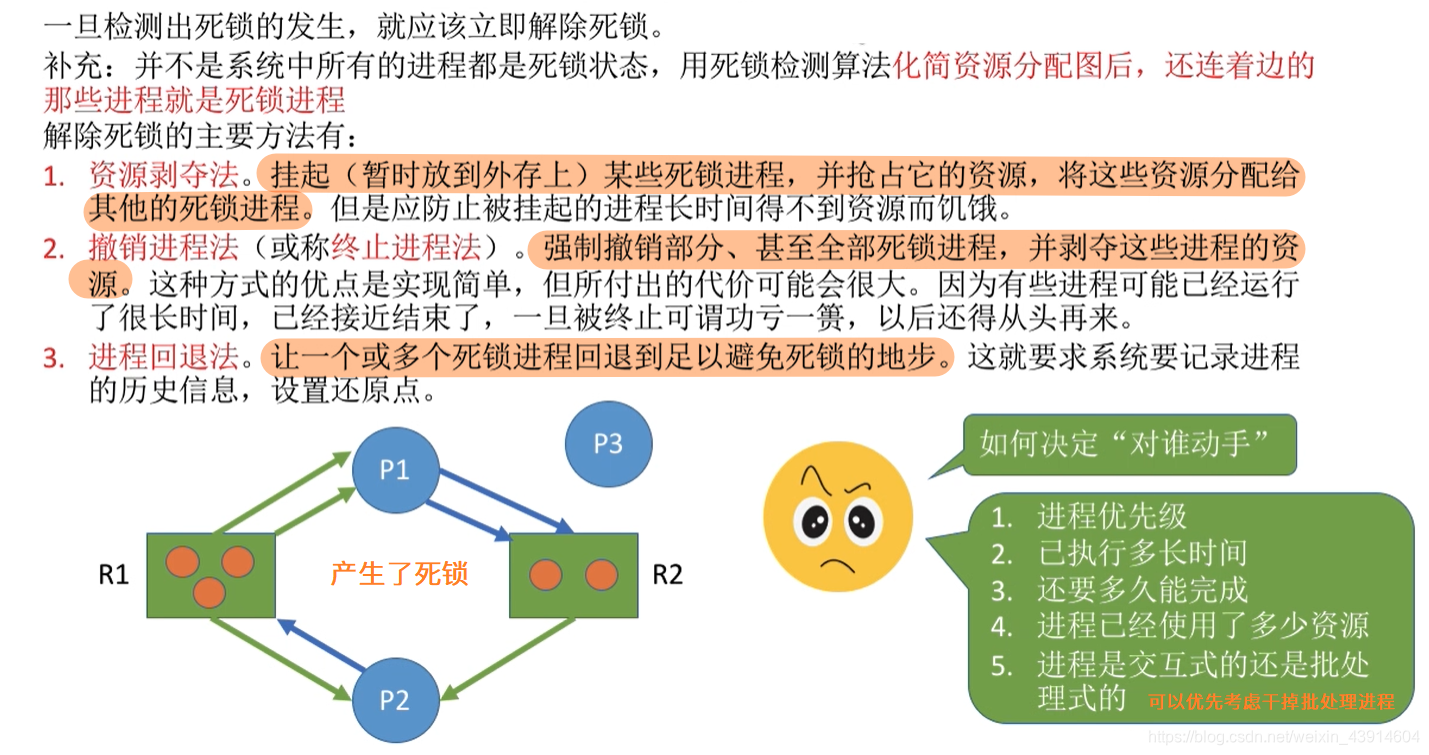
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

一、信号基本运算的MATLAB实现

信号基本运算是乘法、加法、尺度、反转、平移、微分、积分，实现方法有数值法和符号法。
案例一：f(t)为三角信号，求f(2t) , f(2-2t)

 t=-3:0.001:3;
ft=tripuls(t,4,0.5); 
subplot(3,1,1);                                                                           
plot(t,ft);  grid on;
title ('f(t)');
ft1= tripuls(2*t,4,0.5);
subplot(3,1,2);                                                                           
plot(t,ft1);  grid on;
title ('f(2t)');
ft2= tripuls(2-2*t,4,0.5);
subplot(3,1,3);                                                                           
plot(t,ft2);  grid on;
title ('f(2-2t)');

案例二：已知f1(t)=sinwt , f2(t)=sin8wt , w=2pi , 求f1(t)+f2(t)和f1(t)f2(t) 的波形图

w=2*pi;
t=0:0.01:3;
f1=sin(w*t);
f2=sin(8*w*t);
subplot(211)
plot(t,f1+1,':',t,f1-1,':',t,f1+f2)
grid on,title('f1(t)+f2(t))')
subplot(212)
plot(t,f1,':',t,-f1,':',t,f1.*f2)
grid on,title('f1(t)*f2(t)')

二、计算两信号的卷积积分

卷积积分

信号的卷积是数学上的一种积分运算，两个信号的卷积定义为：

信号的卷积运算在系统分析中主要用于求解系统的零状态响应。一般情况，卷积积分的运算比较困难，但在MATLAB中则变得十分简单，MATLAB中是利用conv函数来实现卷积的。

格式：g=conv(f1,f2) 
说明：f1=f1(t),f2=f2(t) 表示两个函数，g=g(t)表示两个函数的卷积结果。

案例一：

f1（t）=ε(t-1)-ε(t-2)
f2（t）=ε(t-2)-ε(t-3)
求卷积g（t）=f1（t）*f2（t）

代码：

t1=1:0.01:2; t2=2:0.01:3;
t3=3:0.01:5;    %两信号卷积结果自变量t区间应为：[两信号起始时刻之%和~两信号终止时刻之和]请自行推导该结论
f1=ones(size(t1));  %高度为一的门函数，时间从t=1到t=2
f2=ones(size(t2));  %高度为一的门函数，时间从t=2到t=3
g=conv(f1,f2);       %对f1和f2进行卷积
subplot(3,1,1),plot(t1,f1);  %画f1的波形
subplot(3,1,2),plot(t2,f2);  %画f2的波形
subplot(3,1,3),plot(t3,g);    % grid on; 画g的波形

运行结果：

案例二：

f1（t）=ε(t+1)-ε(t)
f2（t）=ε(t)-ε(t-1)
求卷积g（t）=f1（t）*f2（t）

代码：

t1=-1:0.01:0; t2=0:0.01:1;
t3=-1:0.01:1;   
f1=ones(size(t1)); 
f2=ones(size(t2)); 
g=conv(f1,f2);     
subplot(3,1,1),plot(t1,f1); 
subplot(3,1,2),plot(t2,f2);
subplot(3,1,3),plot(t3,g); 

运行结果；

案例三：

t=0:0.01:5;
t1=0:0.01:10;
f1=t;
f2=t.*exp(-t);
g=conv(f1,f2); 
subplot(3,1,1),plot(t,f1);
subplot(3,1,2),plot(t,f2);
subplot(3,1,3),plot(t1,g);

运行结果：

t=-5:0.01:0;
t1=-10:0.01:0;
f1=0;
f2=t.*exp(t);
g=conv(f1,f2); 
subplot(3,1,1),plot(t,f1);
subplot(3,1,2),plot(t,f2);
subplot(3,1,3),plot(t1,g);

三、两序列的卷积和

已知 f1（k）={1,1,1,2},f2(k)={1,2,3,4,5}求卷积和

x=[1,1,1,2];
h=[1,2,3,4,5];
y=conv(x,h);      
stem(y);         
axis([-1,10,-20,20]); 

运行结果：