文章目录

2.1 算法解释
2.2 分配问题
- 455. 分发饼干（简单）
- 135. 分发糖果（困难）
2.3 区间问题
- 435. 无重叠区间（中等）
2.4 练习
- 605. 种花问题（简单）
- 452. 用最少数量的箭引爆气球（中等）
- 763. 划分字母区间（中等）
- 122. 买卖股票的最佳时机 II （中等）
- 406. 根据身高重建队列（中等）
- 665. 非递减数列（中等）
2.5 总结

2.1 算法解释

顾名思义，贪心算法或贪心思想采用贪心的策略，保证每次操作都是局部最优的，从而使最后得到的结果是全局最优的。

2.2 分配问题

455. 分发饼干（简单）

在这里插入图片描述

题解

因为饥饿度最小的孩子最容易吃饱，所以我们先考虑这个孩子。为了尽量使得剩下的饼干可以满足饥饿度更大的孩子，所以我们应该把大于等于这个孩子饥饿度的、且大小最小的饼干给这个孩子。满足了这个孩子之后，我们采取同样的策略，考虑剩下孩子里饥饿度最小的孩子，直到没有满足条件的饼干存在。

简而言之，这里的贪心策略是，给剩余孩子里最小饥饿度的孩子分配最小的能饱腹的饼干。

至于具体实现，因为我们需要获得大小关系，一个便捷的方法就是把孩子和饼干分别排序。这样我们就可以从饥饿度最小的孩子和大小最小的饼干出发，计算有多少个对子可以满足条件。

代码

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        int ans = 0;
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int i = 0;
        for(int biscuit : s){
            if(i < g.size() && biscuit >= g[i]){
                ans ++;
                i ++;
            }
        }
        return ans;
    }
};

135. 分发糖果（困难）

在这里插入图片描述

题解

做完了题目455，你会不会认为存在比较关系的贪心策略一定需要排序或是选择?虽然这一道题也是运用贪心策略，但我们只需要简单的两次遍历即可︰
- 把所有孩子的糖果数初始化为1；
- 先从左往右遍历一遍，如果右边孩子的评分比左边的高，则右边孩子的糖果数更新为左边孩子的糖果数加 1 ；
- 再从右往左遍历一遍，如果左边孩子的评分比右边的高，且左边孩子当前的糖果数不大于右边孩子的糖果数，则左边孩子的糖果数更新为右边孩子的糖果教加1。
- 通过两次遍历分配的糖果就可以满足题目要求了。这里的贪心策略即为，在每次遍历中，只考虑并更新相邻一侧的大小关系。

代码

class Solution {
public:
    int candy(vector<int>& ratings) {
        int n = ratings.size();
        vector ans(n, 1);
        // 从左往右遍历
        for(int i=0; i<n-1; ++i){
            if(ratings[i+1] > ratings[i]){
                ans[i+1] = ans[i] + 1;
            }
        }
        // 从右往左遍历
        for(int i=n-1; i>0; --i){
            // 左边孩子评分比右边孩子高 且 左边孩子糖果数不大于右边孩子   
            if(ratings[i-1] > ratings[i] && ans[i-1] <= ans[i]){
                ans[i-1] = ans[i] + 1;
            }
        }
        for(int i=0; i<n; ++i){
            cout<<ans[i]<<" ";
        }
        int sum = accumulate(ans.begin(), ans.end(), 0);
        return sum;
    }
};

收获
- 复习了 accumulate(ans.begin(), ans.end(), 0);

2.3 区间问题

435. 无重叠区间（中等）

在这里插入图片描述

题解
- 求最少的移除区间个数，等价于尽量多保留不重叠的区间。在选择要保留区间时，区间的结尾十分重要：选择的区间结尾越小，余留给其它区间的空间就越大，就越能保留更多的区间。因此，我们采取的贪心策略为，优先保留结尾小且不相交的区间。
- 具体实现方法为，先把区间按照结尾的大小进行增序排序，每次选择结尾最小且和前一个选择的区间不重叠的区间。我们这里使用C++的Lambda，结合std : :sort()函数进行自定义排序。
- 在样例中，排序后的数组为[[1.2]，[1.3]，[2.4]]。按照我们的贪心策略，首先初始化为区间[1.2];由于[1,3]与[1,2]相交，我们跳过该区间;由于[2.4]与[1,2]不相交，我们将其保留。因此最终保留的区间为[[1,2],[2,4]]。

代码

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), [](vector<int>&a, vector<int>&b){return a[1]<b[1];});
        int ans = 0;
        int prev = intervals[0][1];
        for(int i=1; i<intervals.size(); ++i){
           if(intervals[i][0] < prev){
               ans ++;
           }
           else{
               prev = intervals[i][1];
           }
        }
        return ans;
    }
};

收获
- 复习了对二维数组的第二个维度进行排序的方法：sort(intervals.begin(), intervals.end(), [](vector<int>&a, vector<int>&b){return a[1]<b[1];});

2.4 练习

605. 种花问题（简单）

在这里插入图片描述

题解
- 为了判断能否在不打破规则的情况下种入 n 朵花，从贪心的角度考虑，应该在不打破规则的情况下尽可能地种花，然后判断种入的花是否大于等于 n。
- 为了方便后续判断，可以先设置边界条件，当 i 为 0 的时候，将 prev 设置为 0；当 i 为 1 的时候，将 later 设置为 0；
- 遍历数组的时候，如果当前遍历到的值为 0 ，说明可能可以种花，此时继续判断它的 prev 和 later 是否也都是 0，如果符合条件，那么说明此处可以种下一朵花， n – ；如果当前遍历到的值为 1 ，说明这个地方和下一个位置都不能种花，那就直接跳过两个位置，i++ ，for 循环里会再自加一次，因此一共自加了两次。
- 最后判断 n 是否小于等于 0 ，表示能够在不打破规则的情况下种入 n 多花，否则表示不能，返回 false。

代码

class Solution {
public:
    bool canPlaceFlowers(vector<int>& flowerbed, int n) {
        int len = flowerbed.size();
        for(int i=0; i<len; ++i){
            int prev = i == 0? 0 : flowerbed[i-1];
            int later = i == len-1? 0 : flowerbed[i+1];
            if(flowerbed[i] == 0){
                if(!prev && !later){
                    n-- ;
                    flowerbed[i] = 1;
                }
            }
            if(flowerbed[i] == 1)
                ++i;
        }
        return n<=0;
    }
};

收获
- 能够模仿着前几天的题设置边界条件。

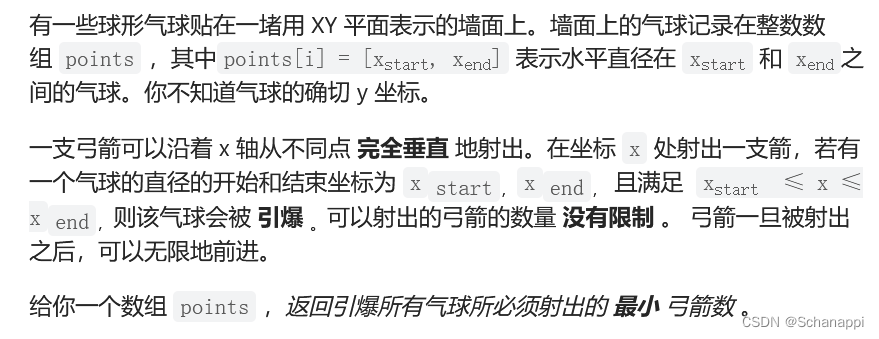
452. 用最少数量的箭引爆气球（中等）

在这里插入图片描述

题解
- 这道题和 435 类似，但是这道题需要按照区间开头排序。
- 重叠的区间用一支箭就可以引爆，不重叠的区间需要单独用一根箭引爆。求最小的弓箭数，等价于求尽可能多的区间重叠个数。
- 选择区间左端升序排序，然后判断当前区间是否和上一个区间有重叠 if(points[i][0] <= prev)，需要满足当前区间的左边界 <= 上一区间的右边界。
  - 如果存在重叠，说明这两个区间用一支箭就可以引爆。由于加入了新的区间，此时需要更新更新右边界，prev = min(prev, points[i][1]); 。
  - 如果不存在重叠，那么当前区间和上一区间需要用不同的箭引爆，因此箭的数量 ans ++，更新上一个区间的右边界 prev = points[i][1]; 。

代码

class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        int ans = 1;
        sort(points.begin(), points.end());
        int prev = points[0][1];
        for(int i=1; i<points.size(); ++i){
            if(points[i][0] <= prev){
                prev = min(prev, points[i][1]);
            }
            else{
                ans ++;
                prev = points[i][1];
            }
        }
        return ans;
    }
};

收获
- 这道题我用了左端升序排序，但是题解很多用右端升序排序。不过思路都是类似的，就不多做记录了。

763. 划分字母区间（中等）

在这里插入图片描述

题解
- 划分字符串，要得到尽可能多的片段，并且同一字母只能出现在一个片段中。因此每个片段要尽可能小，也就是说一个片段中包含尽可能少的字母，那么就能得到尽可能多的片段。
- 考虑某个字符 ch ，使用函数 s.find_first_of(ch) 找到该字符第一次出现的位置，记为 begin ，使用函数 s.find_last_of(ch) 找到该字符最后一次出现的位置，记为 end ，这样就划分出了一个片段。
- 接着考虑 [begin, end] ，判断其中包含的字符是否仅出现在这个片段 ，通过 pos = s.find_last_of(ch) 来确定该字符最后一次出现的位置，并与 end 做比较，如果end < pos，说明该字符在该片段后还有出现，此时需要更新 end ，扩大片段范围，end = max((int)s.find_last_of(s[i]), end); 。
- 在扩大片段范围的过程中，为了不重复判断同一字符，我使用了哈希表 cnt 来记录字符是否出现过。
- 当一次 for 循环结束，说明我们找到了当前可划分的最小片段，此时我们计算该片段的长度，并存入答案数组 ans 中。如果当前已经把整个字符串 s 都遍历了，那么直接返回答案数组；否则更新下一个片段的第一个字符 ch = s[end + 1];。

代码

class Solution {
public:
    vector<int> partitionLabels(string s) {
        vector<int> ans;
        vector<int> cnt(26);
        char ch = s[0];
        cnt[ch - 'a'] = 1;
        while(1){
            int start = s.find_first_of(ch);
            int end = s.find_last_of(ch);
            for(int i=start+1; i<=end; ++i){
                if(!cnt[s[i] - 'a']){
                    // 说明还未遍历
                    end = max((int)s.find_last_of(s[i]), end);
                    // int newEnd =  s.find_last_of(s[i]);
                    // if(newEnd > end)   end = newEnd;
                    cnt[s[i] - 'a'] = 1;
                }
            }
            ans.push_back(end - start + 1);
            if(end == s.size() - 1) return ans;
            ch = s[end + 1];
        }
    }
};

收获
- 这道题学习了 string.find() 的变形，也就是 s.find_first_of() 和 s.find_last_of() ，但是它们的返回类型为size_type ，并不是完全等同于 int ，因此在判断是否更新 end 的时候，需要将返回值强制转换成 int ，才可以使用 max 函数。

122. 买卖股票的最佳时机 II （中等）

在这里插入图片描述

题解
- 如果要使得利润最大，那么就要使能够产生利润的两个天数差距越小，也就是卖出的时间尽可能接近购买的时间，为后续利润增加留出更多的空间。
- 这里我用 prev 记录前一天的价格，如果当天价格 prices[i] 大于 prev ，说明这时候卖出去会产生利润，因此更新当前的利润值，并更新 prev ，prev = prices[i]; ，注意，由于题目中提到在当天抛售完这支股票后可以再次买入，因此无论当天是否售出股票，都要更新 prev 为当天的价格。

代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int ans = 0;
        int n = prices.size();
        int prev = prices[0];
        for(int i=1; i<n; ++i){
            if(prices[i] > prev){
                ans += prices[i] - prev;
            }
            prev = prices[i];
        }
        return ans;
    }
};

收获
- 这题一开始我还复杂化了，想着要去排序，然后使用字典记录价格和对应的时间，事实上简单很多。
- 看了一下题解，有一个值得理清的点，利润增加可以分成两种情况：
  - 单独交易日，当天买入，隔天售出：profit = prices[i] - prices[i-1];
  - 连续上涨交易日，当天买了，隔几天才售出，profit = prices[i] - prices[j] = (prices[i] -prices[i-1]) + (prices[i-1] - prices[i-2]) + ... + (prices[j+1] - prices[j])
    
    这个公式佐证了我的题解的正确性。

406. 根据身高重建队列（中等）

在这里插入图片描述

题解
- 题目的意思不难理解，面对有两个维度的贪心问题，通常有个诀窍：其中一个维度按照升序排序，另外一个维度按照降序排序。
- 这道题可以选择按照 h 降序排序，按照 k 升序排序。
  - 按照 h 降序排序，可以保证后面加入的元素都不会影响当前元素的位置；
  - 按照 k 升序排序，既减少了插入的次数，也保证了正确性。比如 [5,2] , [5,3] ，如果我们按照 k 降序排序的话，即 [5,3], [5,2]，先将 [5,3] 插入在 idx = 3 的位置上，再将 [5,2] 插入在 idx = 2 的位置上，此时 [5,3] 前面就有 4 个大于或等于它的元素，和自身位置矛盾。
- 对于答案数组，如果当前元素的 k 大于或等于 ans 的长度，说明前面元素的个数还没有超过当前元素的 k，所以该元素可以直接插入到 ans 的末尾；否则 ans 插入到 index = k 的位置上。

代码

class Solution {
public:
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        // 按照第一维度 h 降序，第二维度 k 升序
        sort(people.begin(), people.end(), [](const vector<int> &a, const vector<int> &b){
            if(a[0] == b[0])    return a[1] < b[1];
            return a[0] > b[0];
        });
        vector<vector<int>> ans;
        for(auto p : people){
            if(p[1] < ans.size()){
                // 插入
                ans.insert(ans.begin() + p[1], p);
            }
            else ans.push_back(p);
        }
        return ans;
    }
};

收获
- 学会了二维数组的贪心处理诀窍，对两个维度都要排序；
- insert 函数的使用：ans.insert(ans.begin() + p[1], p); ；
- 二维数组也是可以直接插入它的元素，无需再转换成一维数组，上次我可能是混淆了，比如 for(auto p : people) ，p 已经是一维数组了。

665. 非递减数列（中等）

在这里插入图片描述

题解
- 非递减数列，其实就是不严格的单调递增序列，只需要满足 nums[i] <= nums[i+1] 即可。对于这道题，其实就是求出将该数组变成非递减数列所需要的最小次数，那么为了使得元素的改变次数最小，对于不满足题目要求的元素，如nums[i] > nums[i+1] ，我们就将其改为 nums[i] = nums[i+1] 。
- 对于nums[i] > nums[i+1] 这种情况，我们既可以改变 nums[i] ，也可以改变 nums[i+1] 。因此我们分成两种情况考虑：
  - 从前往后遍历，改变 nums[i+1] ；
  - 从后往前遍历，改变 nums[i] 。
- 最后取两种遍历情况改变元素的最小值，判断它是否 >= 1 。

代码

class Solution {
public:
    bool checkPossibility(vector<int>& nums) {
        int cnt1 = 0, cnt2 = 0;
        int n = nums.size();
        vector<int> copy(n);
        copy = nums;
        for(int i=0; i<n-1; ++i){
            if(nums[i] > nums[i+1]){
                ++ cnt1;
                nums[i+1] = nums[i]; 
            } 
        }
        for(int i = n-1; i>0; --i){
            if(copy[i] < copy[i-1]){
                ++ cnt2;
                copy[i-1] = copy[i]; 
            }
        }
        return min(cnt1, cnt2) <= 1;
    }
};

收获

看了题解的另外一种思考方法，每次考虑连续的 3 个元素，遵循以下两个原则：

需要尽可能不放大nums[i + 1]，这样会让后续非递减更困难；
如果缩小nums[i]，但不破坏前面的子序列的非递减性；

if (nums[i] > nums[i + 1])  // 出现递减
{
	if (flag)   // 如果还有修改机会，进行修改
  	{
	    if (nums[i + 1] >= nums[ i - 1])// 修改方案1
			nums[i] = nums[i + 1];
      	else                            // 修改方案2
        	nums[i + 1] = nums[i];      
         	flag = false;                   // 用掉唯一的修改机会
     }   
else        // 没有修改机会，直接结束
	return false;