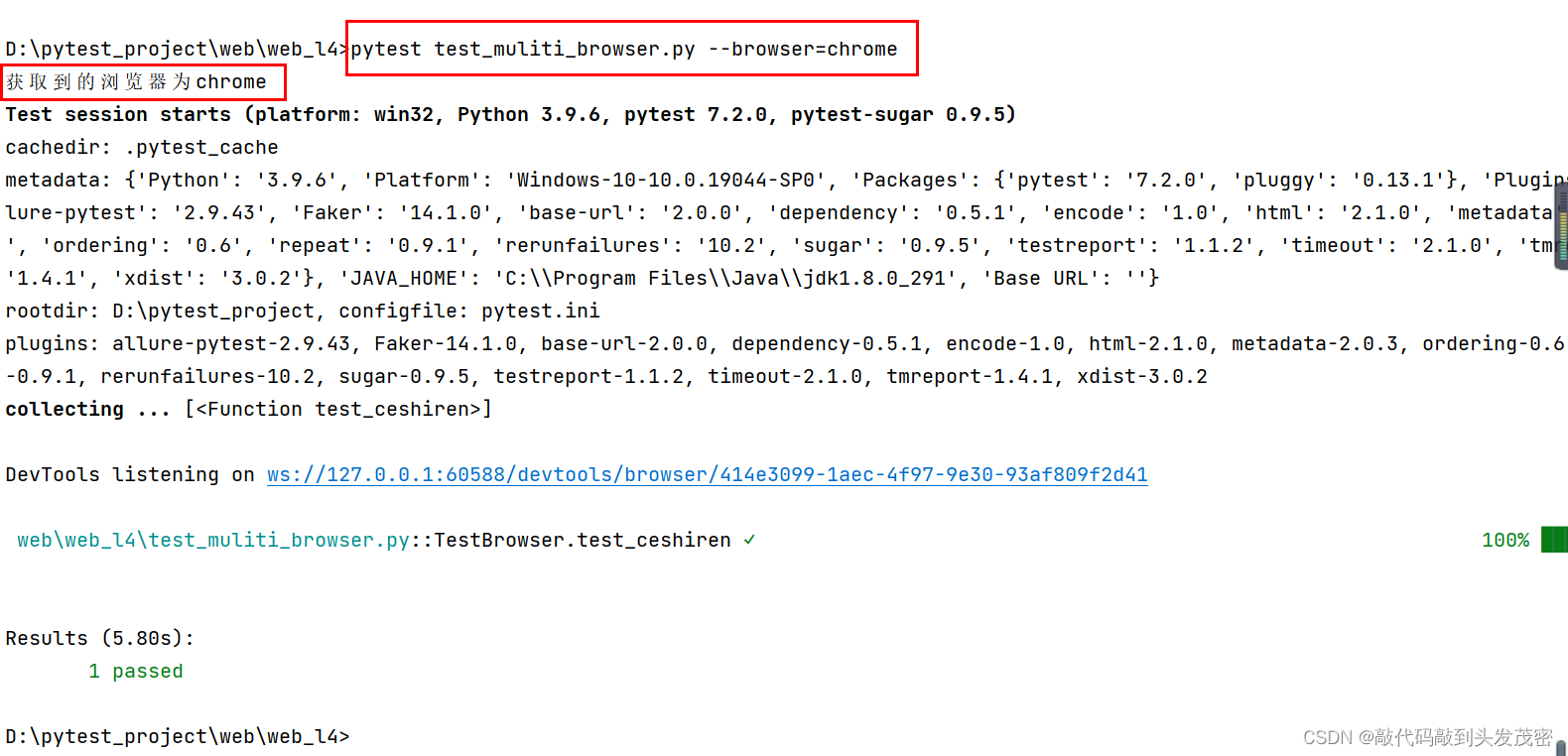
以鸢尾花数据集为例,实现PLS-DA降维,画出降维后数据的散点图并求其方差贡献率。
效果图
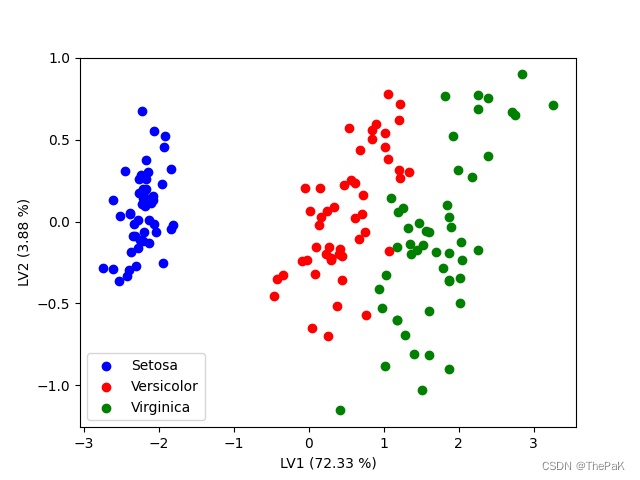
完整代码
# 导入所需库
import numpy as np
from sklearn.cross_decomposition import PLSRegression
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
# 载入数据
iris = load_iris()
X = iris.data
y = iris.target
print(X.shape)
print(y.shape)
# 标准化数据
X = StandardScaler().fit_transform(X)
# 定义PLS-DA对象并拟合数据
plsda = PLSRegression(n_components=2)
plsda.fit(X, y)
# 得到PLS-DA降维后的数据
X_plsda = plsda.transform(X)
print(X_plsda.shape)
# 绘制散点图
colors = ['blue', 'red', 'green']
labels = ['Setosa', 'Versicolor', 'Virginica']
for i in range(len(colors)):
x = X_plsda[:, 0][y == i]
y_plot = X_plsda[:, 1][y == i]
plt.scatter(x, y_plot, c=colors[i], label=labels[i])
# 输出成分贡献率
# 计算PLS-DA成分贡献率
# 计算PLSDA的旋转系数
plsda_components = plsda.x_rotations_
print(plsda_components)
plsda_scores = X_plsda
# 计算PLSDA成分解释的方差比例
variance_explained = np.var(plsda_scores, axis=0) # 计算在PLSDA成分上解释的方差
print("variance_explained shape:", variance_explained.shape)
print("variance_explained:", variance_explained)
total_variance = np.var(X, axis=0) # 计算在原始数据上总方差的和
print("total_variance shape:", total_variance.shape)
print("total_variance:", total_variance)
plsda_variance_ratio = variance_explained / total_variance.sum()
print("total_variance.sum():", total_variance.sum()) # 计算PLSDA成分解释的方差比例
# print(plsda_variance_ratio)
# 输出成分贡献率
for i, ratio in enumerate(plsda_variance_ratio):
print(f'PLS-DA Component {i + 1}: {ratio * 100:.2f}%')
plt.xlabel('LV1 ({} %)'.format(round(plsda_variance_ratio[0] * 100, 2)))
plt.ylabel('LV2 ({} %)'.format(round(plsda_variance_ratio[1] * 100, 2)))
plt.legend()
plt.show()代码解析
主要解析求成分贡献率的过程:
plsda_components = plsda.x_rotations_
plsda_scores = X_plsda
variance_explained = np.var(plsda_scores, axis=0)
total_variance = np.var(X, axis=0)
plsda_variance_ratio = variance_explained / total_variance.sum()
plsda.x_rotations_:plsda是进行PLS-DA的对象,plsda.x_rotations_是PLS-DA模型中X变量(即自变量)的旋转矩阵,表示如何将原始数据X映射到新的降维空间中。将该旋转矩阵存储到变量plsda_components中。对于此数据集,得到的plsda_components是4x2的矩阵。
X_plsda:这是使用PLS-DA降维后的X变量数据集,是150×2的矩阵。
variance_explained = np.var(plsda_scores, axis=0):计算每个主成分(即降维后的新变量)在降维后数据中的方差解释比例,存储到变量variance_explained中。这里使用np.var()函数计算方差。由于本次代码是使用PLS-DA将数据降到2维,故得到的variance_explained是一个包含2个元素的一维数组[2.89312513 0.15504989],表示每个特征的方差之和。
total_variance = np.var(X, axis=0):计算原始数据X中每个变量的总方差,存储到变量total_variance中。原始数据是150×4的矩阵,故total_variance是一个包含4个元素的一维数组,[1. 1. 1. 1.]。
plsda_variance_ratio = variance_explained / total_variance.sum():计算每个主成分在总方差中的方差解释比例,即PLS-DA的方差解释比例。将结果存储到变量plsda_variance_ratio中。total_variance.sum()是求总方差的和,即每个变量的方差之和。这里total_variance.sum()等于3.9999999999999987而不是4,是由于浮点数的存储方式,在某些情况下,计算机无法精确表示某些小数。所以此计算步骤为[2.89312513/3.9999999999999987, 0.15504989/3.9999999999999987]得到[0.72328128 0.03876247],也就是每个主成分在总方差中的方差解释比例。