六个标准数据类型中是序列的有：字符串（String）、列表（List）、元组（Tuple）。

通过索引和切片的方式可以访问序列中的元素。

一、序列索引

序列中的每一个元素都有一个属于自己的编号，我们称为索引（index）。通过索引，我们可以访问序列中的某个元素。

序列索引又分为正向索引和反向索引。

• 正向索引：从起始元素开始，索引值从0开始编号，从左向右索引值持续递增。
• 反向索引：从最后一个元素开始，索引值从-1开始编号，从右向左索引值持续递减。

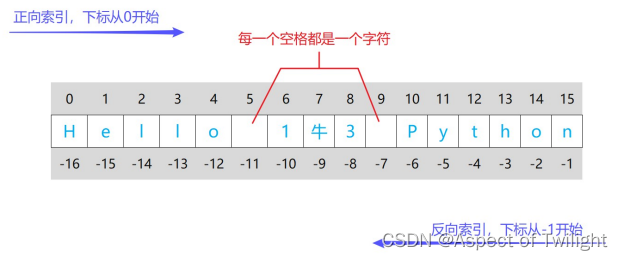
"""字符串序列索引"""
string = "Hello 1牛3 Python"
print(string[0])  # "H"
print(string[-11])  # " "
print(string[10])  # "P"
print(string[-1])  # "n"
print(string[4])  # "o"
print(string[-7])  # " "


"""列表序列索引"""
list1 = ["H", "e", "l", "l", "o", " ", "1", "牛", "3", " ", "P", "y", "t", "h", "o", "n"]
print(list1[0])  # "H"
print(list1[-11])  # " "
print(list1[10])  # "P"
print(list1[-1])  # "n"
print(list1[4])  # "o"
print(list1[-7])  # " "


"""元组序列索引"""
tup = ("H", "e", "l", "l", "o", " ", "1", "牛", "3", " ", "P", "y", "t", "h", "o", "n")
print(tup[0])  # "H"
print(tup[-11])  # " "
print(tup[10])  # "P"
print(tup[-1])  # "n"
print(tup[4])  # "o"
print(tup[-7])  # " "

二、序列切片

• 格式：[起始索引 : 结束索引 : 步长]（注意：所有符号都是英文输入法下的）。
• 从序列中截取起始索引到结束索引的那部分子序列，包括起始索引，但不包括结束索引。
• 当起始索引没有指定时，默认为0，当结束索引没有指定时，默认为序列的长度（前提：步长为正）。
• 步长不写默认为1，代表切片时索引依次+1来选择元素，如果步长为2，则切片时索引依次+2来选择元素；如果步长为负数，则从后面开始切片，索引依次做减法。

"""字符串序列切片"""
string = "Hello 1牛3 Python"
print(string[0: 2])  # "He"
print(string[: 2])  # "He"
print(string[1: 16])  # "ello 1牛3 Python"
print(string[1:len(string)])  # "ello 1牛3 Python"
print(string[1:])  # "ello 1牛3 Python"
print(string[:])  # "Hello 1牛3 Python"
print(string[:1000])  # "Hello 1牛3 Python"
print(string[-11: -9])  # "1"
print(string[2: 6])  # "llo "
print(string[-9: -5])  # "牛3 P"
print(string[1: 10: 2])  # "el 牛 "

"""列表序列切片"""
list1 = ["H", "e", "l", "l", "o", " ", "1", "牛", "3", " ", "P", "y", "t", "h", "o", "n"]
print(list1[0: 2])  # ['H', 'e']
print(list1[-11: -9])  # [' ', '1']
print(list1[2: 6])  # ['l', 'l', 'o', ' ']
print(list1[-9: -5])  # ['牛', '3', ' ', 'P']

"""元组序列切片"""
tup = ("H", "e", "l", "l", "o", " ", "1", "牛", "3", " ", "P", "y", "t", "h", "o", "n")
print(tup[0: 2])  # ('H', 'e')
print(tup[-11: -9])  # (' ', '1')
print(tup[2: 6])  # ('l', 'l', 'o', ' ')
print(tup[-9: -5])  # ('牛', '3', ' ', 'P')
print(tup[: 2])  # ('H', 'e')
print(tup[: 11])  # ('H', 'e', 'l', 'l', 'o', ' ', '1', '牛', '3', ' ', 'P')
print(tup[:])  # ('H', 'e', 'l', 'l', 'o', ' ', '1', '牛', '3', ' ', 'P', 'y', 't', 'h', 'o', 'n')
print(tup[::2])  # ('H', 'l', 'o', '1', '3', 'P', 't', 'o')
print(tup[::-1])  # ('n', 'o', 'h', 't', 'y', 'P', ' ', '3', '牛', '1', ' ', 'o', 'l', 'l', 'e', 'H')
print(tup[::-2])  # ('n', 'h', 'y', ' ', '牛', ' ', 'l', 'e')

Note：len(s)

• 返回对象的长度（元素个数）。
• s可以是序列（如string、bytes、tuple、list或range等）或集合（如dictionary、set或frozenset等）。

print(len("abcd"))  # 4
print(len([1, 2, 3, 4]))  # 4
print(len((1, 2, 3, 4)))  # 4

三、索引会降维，切片不会降维

所谓维度，在物理学和哲学的领域内，指独立的时空坐标的数目。

• 0维是一个无限小的点，没有长度。
• 1维是一条无限长的直线，只有长度。
• 2维是一个平面，是由长度和宽度(或部分曲线)组成面积。
• 3维是2维加上高度组成体积。

在序列索引和序列切片中，我们可以将维度的概念进行类比。

• 一个元素就是0维，如1, 2, 3, 4每个元素就是0维。
• 一个序列就是1维，如[1, 2, 3, 4]一个列表就是1维。
• 一个某元素为序列的序列就是2维，如[[1, 2, 3, 4], [5, 6, 7, 8]]多个列表构成的列表就是2维。

由于序列索引是取出序列中某个特定的元素，因此发生了降维。由于序列切片是取出序列中的某个片段，仍然是同类型的序列，因此并未降维。

list1 = [1, 2, 3, 4]
list2 = [[1, 2, 3, 4],
         [5, 6, 7, 8]]

"""索引会降维"""
print(list1[2])  # 3；list1是1维，3是0维
print(list2[1])  # [5, 6, 7, 8]；list2是2维，[5, 6, 7, 8]是1维
print(list2[1][2])  # 7；list2是2维，7是0维

"""切片不会降维"""
print(list1[:2])  # [1, 2]；list1是1维，[1, 2]是1维
print(list2[:1])  # [[1, 2, 3, 4]]；list2是2维，[[1, 2, 3, 4]]是2维
print(list1[:1])  # [1]；list1是1维，[1]是1维
print(list2[:1][:2])  # [[1, 2, 3, 4]]；list2是2维，[[1, 2, 3, 4]]是2维；等价写法如下
res = list2[:1]  # [[1, 2, 3, 4]]；注意是切片，仍然是2维，不要忘记外面2层[[]]
print(res[:2])  # [[1, 2, 3, 4]]