2018年第八届MathorCup高校数学建模挑战赛
C题 陆基导弹打击航母的数学建模与算法设计
原题再现:
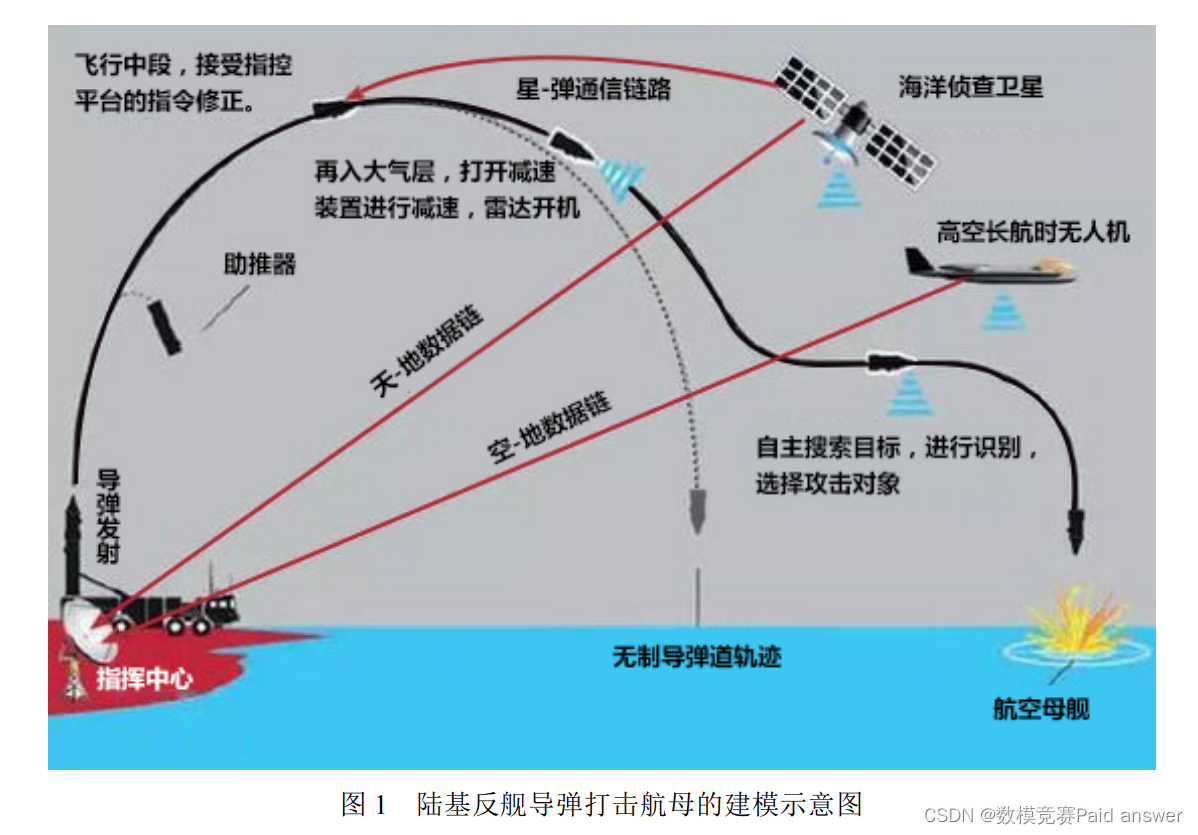
火箭军是保卫海疆主权的战略力量,导弹是国之利器。保家卫国,匹夫有责。为此,请参赛者认真阅读"陆基反舰导弹打击航母的建模示意图"。(附图 1 )参考图中的描述, 请根据如下的已知条件和有关数据, 设计导弹运行的数学模型及其命中目标的算法。导弹发射车初始位置坐标已知为东经120’o30’‘0’“, 北纬 27’o30’'0^” , 它可直接设为导弹打击航母的坐标系原点。

(2) 导弹运行的轨道曲线划分为发射段, 中段和末段。发射段通常为抛物线, 发射速度为 500m/s 。中段可设计为不同的飞行轨道, 由导弹的飞行参数制导所确定。末段最高速度可达到 1000m/s 。导弹末段飞行时间一般不超过 20 秒。三段曲线的衔接点是光滑的 ( 即曲线连续且一阶导数存在), 也就是说导弹飞行的轨道曲线是连续和光滑的, 不能折线飞行。
(3) 导弹运行的轨道曲线需考虑应对敌方反导系统拦截问题, 期望给出难以拦截的攻击曲线。
(4) 地面指挥中心提供给导弹中段轨道的制导数据; 而末段则是由导弹自主攻击航母目标。
(5) 其它复杂环境及气象等影响暂且简化。
(6) 解题中可局部自主创新添加合理假设。
(7) 在建模设计的计算中,根据坐标计算距离时,设定地球半径为 6300km,距离的计算精度要求为 m 级。
根据以上已知数据和条件要求, 请你运筹帷幄, 决胜千里, 创新设计出你的陆基反舰导弹打击航母的运行轨道数学模型, 论述你的算法步骤。包括:
问题 1: 建立初始状态下, 反舰导弹打击航母的静态轨道模型。即 t=0 时, 连接导弹初始位置与航母坐标之间的轨道曲线模型。
问题 2: 在航母按照已知条件 ( 2 ) 给出的航向和速度的航行状态下, 设计导弹飞行的中段动态模型方程和算法步骤。中段通常以发射段的抛物线顶点为起始点。
问题 3: 讨论你所设计的导弹打击航母的轨道曲线的误差分析和命中率分析。
整体求解过程概述(摘要)
随着军事力量的发展,导弹成为现代战争中极具威胁性的进攻型武器。航母作为可以整合通讯、情报、反潜反导装置、作战信息和后勤保障的大型海上战斗机移动基地平台,航母对国家安全带来威胁。导弹打击航母技术对保卫国家安全显得尤为重要。
关于问题一,在初始时刻时,将反舰导弹打击航母分为四个阶段:主动段、被动段、中段变轨、末段。首先考虑地球为自旋椭球,建立地心坐标系和发射坐标系,在两个坐标系相互转换进行计算。在地心坐标系中计算反舰导弹所受引力、科氏力等,根据力与加速度,加速度与速度的力学模型建立微分方程。由于反舰导弹的速度矢量、合力矢量以及加速度矢量等参数不断随时间变化,则可根据速度、位移、加速度关系可建立差分方程,通过迭代即可计算出主动段、被动段反舰导弹的轨迹方程。中段时,考虑到敌方的反导系统拦截,参考助推滑翔模型设计中段轨道曲线,即间歇性的给反舰导弹一个与重力加速度反向的加速度,使其进行变轨,以可靠的级间分离和头体分离飞行条件和合适的再入条件作为限制,然后通过不断优化得出反舰导弹中段变轨部分的运行轨迹。末段时,为增加导弹突破面防御系统能力以及敌方的预测难度,使反舰导弹末端机动具有如伪螺旋形轨道模型。从而得到反舰导弹打击航母的静态轨道模型,以 83.75°的发射仰角飞行1153s,主动段高度为61764m,最高点高度为494833m,再入层高度为142397m,末段最大速度为 773m/s。
关于问题二,反舰导弹中段飞行时,建立实时监测反馈系统。在敌方航母航行参数为未知的情况下,将问题所述航行参数作为侦察卫星和无人机时刻收集的数据并反馈给导弹和地面控制中心,反舰导弹根据航母时刻变化的位置信息改变轨道。此时,反舰导弹相对于静态轨道模型会增加一个与海平面平行的指向航母的加速度矢量,从而消除航母移动带来的影响。考虑到导弹与航母的追及问题,建立差分迭代算法模型,根据导弹飞行各阶段的限制条件,可优化得到反舰导弹动态打击航母的动态轨道模型,以 83.75°的发射仰角飞行 881s,主动段高度为61714m,最高点高度为 493875m,再入层高度为 162784m,末段最大速度为 973m/s。
关于问题三,在反舰导弹飞行中,影响导弹捕捉概率大小的因素有目标指示精度误差、侧向横移误差和目标机动产生的误差,前两者随机性太强,因此本文中只需考虑后者以及主动段飞行参数带来的影响。导弹末端制导取决于雷达搜索范围,在距航母大概20km~30km时,导弹末段雷达开机,发射电磁波,进行搜索制导,将已知经验搜索范围的角度𝜃1与反舰导弹速度矢量和导弹与航母连线矢量的角度𝜃2进行比较,𝜃2 > 𝜃1即为命中。本团队对各参数进行稳定性和灵敏度分析,模型稳定性较高,鲁棒性强。计算误差情况下的制导成功率为 96.97%,命中率为 79.71%。
模型假设:
1.忽略复杂环境、突发事件以及气象条件的影响。
2.控制系统响应速度和精度能够满足末制导雷达指令对弹体控制的要求。
3.导弹飞行中忽略因燃料而引起的质量变化,且导弹飞行过程中能实时接收信号。
4.假设燃料充足,反舰导弹打击航母的过程中不用担心燃料的问题。
5.将地球想象成球体,且因地球地轴与地球自转轴之间的夹角很小可将其忽略。
6.因导弹发射点与航母位置相对地球半径很小而认为发射点的铅垂方向与发射点和航母的方向垂直。
7.静态轨道模型中在中段变轨阶段给反舰导弹的加速度为定值。
问题分析:
陆基导弹分为弹道导弹和巡航导弹,而传统的弹道导弹在燃料燃烧完后只能保持预定的航向,不可改变。初始状态时,即t = 0,海洋侦查卫星和无人机把航母的数据信息传送给导弹发射指挥中心,指挥中心通过计算,设计出一条预定的航向。根据导弹打击航母的过程可以分为发射段、中段以及末段。其中发射段又包括主动段和被动段,主动段时,导弹通过助推器发射,助推器给导弹提供推力,飞行到高空中大约50 km~ 70 km 时[1],导弹将会脱离助推器进入被动段,一段时间后,到达发射段的最高点,导弹开始进入中段。中段初始部分与被动段类似,暂且将其统称为被动段。中段变轨部分,考虑到敌方的反导系统拦截问题,陆基反舰导弹以平衡弹道或跳跃弹道飞行到满足导引头开机点要求的位置和姿态[2],再以一定的攻角再入大气层,然后进行末段制导。在末端制导时,为躲避敌方拦截,反舰导弹末段具有末端机动如蛇形或跃升的攻击能力,这种情况主要是针对敌方的面防御系统。根据导弹脱离助推器前后的受力情况不同,可建立地心坐标系计算出力和加速度的方向,然后转换到发射点坐标系,并据此可以建立微分方程组。根据反舰导弹受力、加速度都随时间变化,可知其速度以及位移也时刻随时间变化,可建立差分方程组,然后根据参数仿真优化得到主动段、被动段、中段变轨、末端制导四个阶段的节点,最后根据所得数据,即可得到反舰导弹打击航母的轨道曲线。
反舰导弹在中段飞行时,无人机根据数据链传来的情报,立即飞往航母上空进行长时间持续跟踪以及准确定位,为反舰导弹的中段机动提供信息支持。反舰导弹接收到信息之后,通过计算,预测航母位置,进行轨道调整,提高打击海上移动航母的命中精度。在航母航行时,由于航母的位置随时间变化,而无人机以及海洋侦查卫星时刻收集航母的位置信息并将信息传递给反舰导弹,反舰导弹根据信息调整轨迹打击航母,建立了一个实时反馈的追及问题模型。航母始终向南航行,反舰导弹在中段的轨迹相对于初始时刻增加了一个平行于海平面并指向航母的加速度,不影响导弹竖直方向速度。使其能够时刻根据航母的位置改变该加速度的方向进而改变反舰导弹的速度并将飞行轨迹不断趋向于航母位置,提高打击航空母舰的精度。
反舰导弹打击航母时,导弹的被动段的运动情况完全取决于导弹的主动段的终点的参数[8]。在标准情况下,导弹始终在主动段的终点速度矢量和地心坐标系中的地心矢径所形成的平面内运动,导弹的着落点和航母所在点重合。但是,实际情况下,考虑到地球的旋转、常值横风的影响、导弹在主动段的运动会受到各种不同的因素的干扰、目标信息迟滞等因素的影响,主动段的终点参数会有偏差,从而产生落点误差,继而会影响命中率。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
The actual procedure is shown in the screenshot
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int n;
cin >> n; //导弹数量
int heigh[n]; //导弹高度
int end[n]; //该枚导弹作为最后击落的导弹时最多击落导弹数量
for (int i = 0; i < n; i++)
{
cin >> heigh[i];
end[i] = 1; //只击落该枚导弹总是可行的
}
for (int i = 0; i < n; i++) //依次把每一枚导弹作为最后一枚
{
for (int j = 0; j < i; j++)
{ //将该枚导弹高度依次与前i枚导弹比较
if (heigh[j] >= heigh[i])
{
end[i] = max(end[i], end[j] + 1);
}
}
}
int maxnum = 0; //最大击落数
for (int i = 0; i < n; i++) //遍历求最大击落数
{
if (end[i] > maxnum)
maxnum = end[i];
}
cout << maxnum;
}