第一题
2578.最小和分割
给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足:
- num1 和 num2 直接连起来,得到 num 各数位的一个排列。
- 换句话说,num1 和 num2 中所有数字出现的次数之和等于 num 中所有数字出现的次数。
- num1 和 num2 可以包含前导 0 。
请你返回 num1 和 num2 可以得到的和的 最小 值。
注意:
- num 保证没有前导 0 。
- num1 和 num2 中数位顺序可以与 num 中数位顺序不同。
示例 1:
输入:num = 4325
输出:59
解释:我们可以将 4325 分割成 num1 = 24 和 num2 = 35 ,和为 59 ,59 是最小和。
示例 2:
输入:num = 687
输出:75
解释:我们可以将 687 分割成 num1 = 68 和 num2 = 7 ,和为最优值 75 。
提示:
- 10 <= num <= 109
思路:
这应该算是个思维题,要把原数拆分成两个数,使得两个数的和最小,那什么情况下最小?比如num=654321,那我们把它变成123+456,就得到最小,即,要满足两个数的位数尽量相同,小数字要在高位。所以我们就可以先获得每一位上的数,将其递增排序,然后将奇数位和偶数位上的数字拼在一起得到两个数,最后得到答案。
代码:
1.C++
class Solution {
public:
int splitNum(int num) {
vector<int> nums;
while(num != 0){
nums.push_back(num % 10);
num /= 10;
}
sort(nums.begin(), nums.end());
int num1 = 0, num2 = 0, len = nums.size();
int i, j;
if(len % 2){
nums.insert(nums.begin(), 0);
len = nums.size();
}
for(i = 0, j = 1; i < len && j < len; i += 2, j += 2){
num1 = num1 * 10 + nums[i];
num2 = num2 * 10 + nums[j];
}
return num1 + num2;
}
};
优化一下
class Solution {
public:
int splitNum(int num) {
string nums = to_string(num);
sort(nums.begin(), nums.end());
int n[2] = {}, t;
for(int i = 0; i < nums.size(); i++){
t = i % 2;
n[t] = n[t] * 10 + nums[i] - '0';
}
return n[0] + n[1];
}
};

2. Python
class Solution:
def splitNum(self, num: int) -> int:
nums = sorted(list(str(num)))
return int(''.join(nums[::2])) + int(''.join(nums[1::2]))
第二题
2579. 统计染色格子数
有一个无穷大的二维网格图,一开始所有格子都未染色。给你一个正整数 n ,表示你需要执行以下步骤 n 分钟:
- 第一分钟,将 任一 格子染成蓝色。
- 之后的每一分钟,将与蓝色格子相邻的 所有 未染色格子染成蓝色。
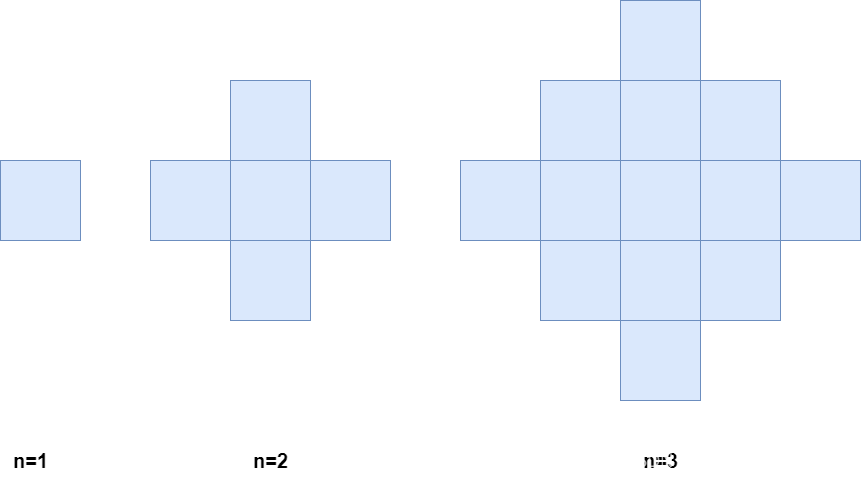
下图分别是 1、2、3 分钟后的网格图。
[https://assets.leetcode.com/uploads/2023/01/10/example-copy-2.png]
请你返回 n 分钟之后 被染色的格子 数目。
示例 1:
输入:n = 1
输出:1
解释:1 分钟后,只有 1 个蓝色的格子,所以返回 1 。
示例 2:
输入:n = 2
输出:5
解释:2 分钟后,有 4 个在边缘的蓝色格子和 1 个在中间的蓝色格子,所以返回 5 。
提示:
- 1 <= n <= 105
思路:
显然,这是一道找数学规律的题,仿佛回到了高中,从第二个开始,可以观察到最中间的一层有 2n - 1个方块,同时往上下分别每层减少两个,也就是2n-1 + (2n-2 + 2n - 4 + … + 1) × 2,所以我们可以模拟这个过程通过累加获得答案,或者直接用等差数列n项和公式并化简一下。
代码:
1.C++模拟
class Solution {
public:
long long coloredCells(int n) {
long long top = 2 * n, res = top - 1;
// cout << top << endl;
for(int i = 1; i < top - 1; i += 2){
res += 2 * i;
}
return res;
}
};
第三题
2580. 统计将重叠区间合并成组的方案数
给你一个二维整数数组 ranges ,其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间(包括二者)的所有整数都包含在第 i 个区间中。
你需要将 ranges 分成 两个 组(可以为空),满足:
- 每个区间只属于一个组。
- 两个有 交集 的区间必须在 同一个 组内。
如果两个区间有至少 一个 公共整数,那么这两个区间是 有交集 的。
- 比方说,区间 [1, 3] 和 [2, 5] 有交集,因为 2 和 3 在两个区间中都被包含。
请你返回将 ranges 划分成两个组的 总方案数 。由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:ranges = [[6,10],[5,15]]
输出:2
解释:
两个区间有交集,所以它们必须在同一个组内。
所以有两种方案:
- 将两个区间都放在第 1 个组中。
- 将两个区间都放在第 2 个组中。
示例 2:
输入:ranges = [[1,3],[10,20],[2,5],[4,8]]
输出:4
解释:
区间 [1,3] 和 [2,5] 有交集,所以它们必须在同一个组中。
同理,区间 [2,5] 和 [4,8] 也有交集,所以它们也必须在同一个组中。
所以总共有 4 种分组方案:
- 所有区间都在第 1 组。
- 所有区间都在第 2 组。
- 区间 [1,3] ,[2,5] 和 [4,8] 在第 1 个组中,[10,20] 在第 2 个组中。
- 区间 [1,3] ,[2,5] 和 [4,8] 在第 2 个组中,[10,20] 在第 1 个组中。
提示:
- 1 <= ranges.length <= 105
- ranges[i].length == 2
- 0 <= starti <= endi <= 109
思路:
根据题目描述的提示,我们可以将这个二维数组中的区间划分成两部分,一部分是互相之间有交集的,他们必须在同一个组,另一部分是相对独立的那些区间,它们可以在两个组中自由分配,进一步,假如我们把那部分互相有交集的区间进行合并,变成一个大区间,那不就是相当于一个大区间和n个独立的小区间吗,而这个大区间又可以看做是和n个小区间相独立的一个区间,因此将独立的区间记为res,则答案就是2res。
所以我们先对二维数组排序,然后从前往后依次遍历数组,统计独立的区间个数,有相交的就将其合并。
代码:
1.C++
class Solution {
public:
int countWays(vector<vector<int>>& ranges) {
sort(ranges.begin(), ranges.end(), [](auto &a, auto &b){
return a[0] < b[0];
});
int right = ranges[0][1], res = 2;
const int MOD = 1e9 + 7;
// res 记录独立的集合数的放法
for(auto pair: ranges){
if(pair[0] > right){
// 说明pair独立
res = (res * 2) % MOD;
}
// 更新right
right = max(pair[1], right);
}
return res;
}
};
2. Python
class Solution:
def countWays(self, ranges: list[list[int]]) -> int:
ranges.sort(key=lambda x: x[0])
res, right = 1, ranges[0][1]
for l, r in ranges:
if l > right:
res += 1
right = max(right, r)
return 2 ** res % (10 ** 9 + 7)

总结
第一题考察思维,第二题考察数学推理,第三题考排序+区间组合,感觉还是比较经典的。最后一题一般不看,最多3题选手。