目录
二叉树
特点
性质
二叉树的创建
声明
创建
-> 成员运算符
批量创建
二叉树的遍历
先序遍历
中序遍历
后序遍历
层序遍历
树的相关术语
特殊二叉树
满二叉树
完全二叉树
二叉树
树(Tree)是n(n≥0)个节点的有限集。在任意一棵树中有且仅有一个特定的称为根(Root)的节点;当n>1时,其余节点可分m(m>0)为个互不相交的有限集T1,T2,...,Tm;其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
二叉树(Binary Tree)是一种特殊的有序树型结构,所有节点最多只有2棵子树。
特点
(1)每个节点至多有两棵子树;
(2)二叉树的子树有左右之分;
(3)子树的次序不能任意颠倒(有序树)。
性质
(1)二叉树的第i层上至多有2^(i-1)个节点(i≥1)。
(2)深度为h的二叉树中至多含有2^h-1个节点(h≥1)。
(3)若在任意一棵二叉树中,有n0个叶子节点,有n2个度为2的节点,则必有n0=n2+1。
(4)具有n个节点的满二叉树深为log2n+1。
(5)若对一棵有n个节点的完全二叉树进行顺序编号(1≤i≤n),
那么,对于编号为i(i≥1)的节点:
当i=1时,该节点为根,它无双亲节点。
当i>1时,该节点的双亲节点的编号为i/2。
若2i≤n,则有编号为2i的左节点,否则没有左节点。
若2i+1≤n,则有编号为2i+1的右节点,否则没有右节点。
二叉树的创建
声明
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};在C/C++语言中,经常使用 NULL 来表示空指针。
NULL在头文件里的定义:
#ifndef NULL
#ifdef __cplusplus
#define NULL 0
#else
#define NULL ((void *)0)
#endif
#endif即在 C++中,NULL 被定义为整形常量 0,而在 C 中,被定义为无类型指针常量 (void*) 0 。
C++11标准增加了新的关键字 nullptr,表示空指针。
建议使用C++11及以上版本的用以下的二叉树声明:
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};创建
#include <iostream>
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->right->left = new TreeNode(4);
root->right->right = new TreeNode(5);
return 0;
}创建结果:
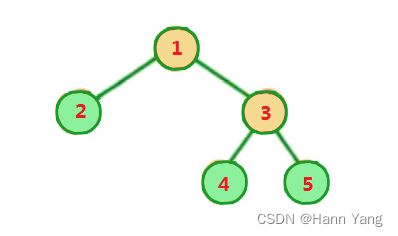
成员运算符->
指向结构体或对象的指针访问其内成员。当一个指针指向一个结构体、对象时,称之为结构体指针或对象指针。结构体指针或对象指针中的值是所指向的结构体或对象的首地址。通过结构体指针或对象指针即可访问该结构体或对象。
结构体指针变量定义的一般形式为:
struct 结构体类型名 *指针名; //结构体指针
struct 结构体类型名 *指针名 = &一个结构体的名字; //结构体指针并赋初值
struct 结构体类型名 *指针名 = new struct 结构体类型名; //结构体指针并用new申请内存
struct 结构体类型名 *指针名 =(struct 结构体类型名 *)malloc(sizeof(struct 结构体类型名))
//结构体指针并用malloc申请内存 使用应包含头文件stdlib.h子树root->left, root->right 还可以 . 运算表示,也成员运算符。两者的区别:
点运算符 . 左边必须用 * 寻址运算符取到指针root指向的结构或者对象实体,如(*root);对比箭头状的成员运算符 -> ,其左边必须为结构体指针,如root。
TreeNode* root = new TreeNode(1);
(*root).left = new TreeNode(2);
(*root).right = new TreeNode(3);
(*(*root).right).left = new TreeNode(4);
(*(*root).right).right = new TreeNode(5);批量创建
上例只是创建5节点,如要建更多节点,这样一个一个增加节点写起来复杂;可以用数组或容器等可迭代数据类型批量来创建。
代码明天补上
二叉树的遍历
指如何按某种搜索路径巡防树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。
常见的遍历方法有:先序遍历,中序遍历,后序遍历,层序遍历。
以一棵满二叉树为例:
_______1________
/ \
__2__ ___3___
/ \ / \
4 5 _6 _7
/ \ / \ / \ / \
8 9 10 11 12 13 14 15先序遍历
若二叉树为空,为空操作;
否则(1)访问根节点;(2)先序遍历左子树;(3)先序遍历右子树。
遍历结果: 1 [2 [4 8 9] [5 10 11]] [3 [6 12 13] [7 14 15] “根左右”

中序遍历
若二叉树为空,为空操作;
否则(1)中序遍历左子树;(2)访问根结点;(3)中序遍历右子树。
遍历结果: [[8 4 9] 2 [10 5 11]] 1 [[12 6 13] 3 [14 7 15]] “左根右”

后序遍历
若二叉树为空,为空操作;
否则(1)后序遍历左子树;(2)后序遍历右子树;(3)访问根结点。
遍历结果: [[8 9 4] [10 11 5] 2] [[12 13 6] [14 15 7] 3] 1 “左右根”

层序遍历
若二叉树为空,为空操作;否则从上到下、从左到右按层次进行访问。
遍历结果: 1 [2 3] [4 5 6 7] [8 9 10 11 12 13 14 15]
代码明天补上
树的相关术语
节点:包含一个数据元素及若干指向其子树的分支,又的译成“结点”(Node)
根:树和子树的“顶点”(Root)
度:节点拥有的子树数量称为节点的度(Degree);树的度是指树内个结点的度的最大值
分支节点:度不为0的节点
叶子:没有子树的节点,即它的度为0 (Leaf)
子节点:结点的子树的根称为该节点的孩子(Child)
父节点:对应子节点上一层(level)节点称为该节点的双亲(Parent)
兄弟结点:同一父节点的子节点,互称兄弟(Sibling)
节点的祖先:是从根到该结点所经分支上的所有节点
节点的子孙:以某结点为根的子树中的所有节点
层:从根开始,根为第一层,根的孩子为第二层...(Level)
深度:树中结点的最大层次数,称为树的深度或高度 (Depth or Height)
森林:是很多互不相交的树的集合(Forest)
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树
有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树
最大树(最小树):每个结点的值都大于(小于)或等于其子结点(如果有的话)值的树
特殊二叉树
满二叉树
所有层的节点都达到最大数量,叶子除外的所有节点都有两个子节点,所有叶子都在最底一层(k)且数目为2^(k - 1)。即深度k且有2^k - 1个节点(叶子“长”满最后一层),或称完美二叉树 (Perfect Binary Tree)
______12_______
/ \
__3__ __5__
/ \ / \
_7 6 _9 11
/ \ / \ / \ / \
13 8 1 4 10 2 0 14完全二叉树
如果删除最底一层的所有叶子它就是满二叉树,即除了最后一层,每层节点都达到最大数量 ,即有深度k的个节点数在左闭右开【2^(k-1)+1,2^k-1】区间内。(Complete Binary Tree)
________3______
/ \
___11___ __4__
/ \ / \
14 7 9 13
/ \ / \ /
2 5 8 6 1
完全二叉树性质:
1. 具有N个节点的完全二叉树的深度为[log2 N]+1,其中[x]为高斯函数,截尾取整。
2. 如果对一棵有n个节点的完全二叉树的节点按层序编号(从第一层到最后一层,每层从左到右),则对任一节点,有:
(1)如果i=1,则节点i是二叉树的根,无双亲;如果i>1,则其双亲节点为[i/2];
(2)如果2i>n,则节点i无左孩子;否则其左孩子是节点2i;
(3)如果2i+1>n,则节点i无右孩子;否则其右孩子是节点2i+1。