本次实验大部分素材来源于山大王成优老师的讲义以及冈萨雷斯(MATLAB版),仅作个人学习笔记使用,禁止用作商业目的。
文章目录
- 一、实验目的
- 二、实验例题
- 1. 数字图像水印技术
- 2. 可见水印的嵌入
- 3. 不可见脆弱水印
- 4. 不可见鲁棒水印
一、实验目的
- 了解数字图像水印技术的基本原理、分类和应用。
- 掌握简单的可见水印和不可见水印的嵌入方法。
- 实现一种基于 DCT 的不可见鲁棒水印,并进行水印鲁棒性测试。
二、实验例题
1. 数字图像水印技术
数字图像水印处理是把数据插入到一幅图像中的过程,以这样的方式对图像内容进行保护。一个典型的图像水印处理系统如图 1 所示。
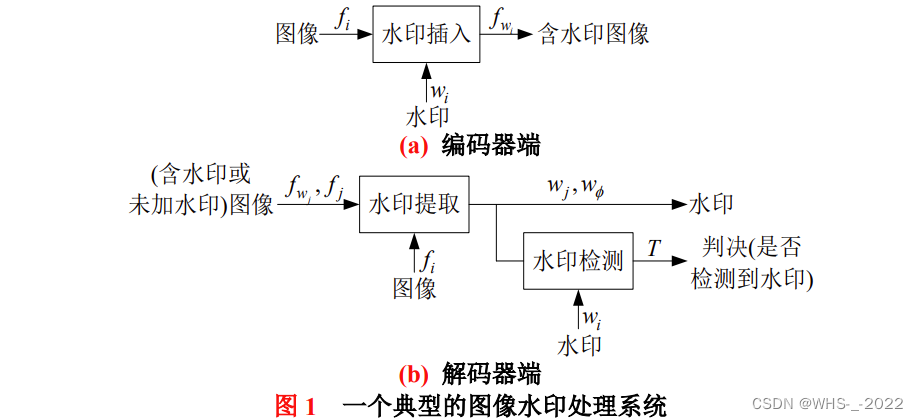
在编码器端,发送者将水印
w
i
w_i
wi 嵌入到原始图像
f
i
f_i
fi
中,产生含水印图像
f
w
i
f_{w_i}
fwi ;在解码器端,接收者提取和验证含水印图像
f
w
i
f_{w_i}
fwi 或 未添加水印图像
f
j
f_j
fj 中水印
w
i
w_i
wi 的存在性。
w
j
w_j
wj 是提取的水印,T 是预定义的阈值。
根据不同的特性,数字水印可以从以下三个方面进行分类:
- 根据水印的鲁棒性,可以将水印分为鲁棒水印和脆弱水印。鲁棒水印是指含水印图像在经过各种处理操作甚至恶意攻击后,隐藏在其中的水印信息仍然可以被提取出来,主要用于版权保护;脆弱水印对图像的变化非常敏感,含水印图像发生变化后将影响水印的检测,从而提示图像已被修改,主要用于图像内容认证。
- 根据水印的可见性,可以将水印分为可见水印和不可见水印。可见水印是一幅不透明或半透明的子图像,它对观察者是可见的,电视网络通常将可见水印放在屏幕的左上角或右下角以证明它的版权归属;不可见水印裸眼是看不见的,但可以通过一个合适的水印提取方法从含水印图像中恢复出水印。
- 根据水印内容,水印又可分为无意义水印和有意义水印。无意义水印对应于一段伪随机序列,通常只能判断图像中是否存在水印,而无法直接观察;有意义水印是指水印本身也是一幅二值图像或者灰度图像,可以从含水印图像中提取并通过观察确认。
2. 可见水印的嵌入
可见水印一般通过与原始图像直接叠加的方式实现嵌入,如式 ( 1 ) (1) (1)所示。水印图像 w w w 通过线性组合的方式嵌入到原始图像 f f f 中,得到含水印图像 f w f_w fw 。
f w = ( 1 − α ) f + α w (1) f_{w}=(1-\alpha) f+\alpha w\tag1 fw=(1−α)f+αw(1)
3. 不可见脆弱水印
在像素深度为 8 位的图像中,最低有效位(Least Significant Bit, LSB)对图像的质量影响较小。利用这种特性可以在不影响原始图像主观质量的情况下,将水印图像插入到原始图像的最低几位有效位中。然而,这种基于 LSB 的水印嵌入法则对诸如 JPEG 压缩、空间滤波等常见的信号处理操作特别敏感,鲁棒性较差。
以图 2 所示的原始 Lena 图像和水印图像为例,式 ( 2 ) (2) (2)给出了一种基于 LSB 的脆弱水印嵌入法则,将水印图像的两位最高有效位(Most Significant Bit, MSB)插入到了 Lena 图像的最低两位有效位中。
f
w
=
4
⌊
f
4
⌋
+
⌊
w
64
⌋
(2)
f_{w}=4\left\lfloor\frac{f}{4}\right\rfloor+\left\lfloor\frac{w}{64}\right\rfloor\tag2
fw=4⌊4f⌋+⌊64w⌋(2)
其中,f 为原始图像,w 为水印图像,f_w 为嵌入水印后的图像,
⌊
⋅
⌋
\lfloor\cdot\rfloor
⌊⋅⌋ 为下取整操作(可用
MATLAB 函数 floor 来实现)。

使用 imwrite 函数进行 JPEG 压缩攻击测试:
A = imread('1.Lena 图像.tif');
imwrite(A, 'JPEG 压缩图像.jpg', 'quality', 80); %80 表示质量因子,其值越小,表示图
像被压缩的越厉害
D = imread('JPEG 压缩图像.jpg');
4. 不可见鲁棒水印
当前,常见的鲁棒水印算法都是在频域中实现水印嵌入的,以经典的基于离散余弦变换(Discrete Cosine Transform, DCT)的鲁棒水印算法为例,主要过程如下:
- 对原始图像进行二维 DCT 变换,DCT 变换具有较好的能量集中特性,可以将
低频能量集中在图像的左上角:
A = imread('3.Lena 图像.tif');
A = double(A);
A_dct = dct2(A); %二维 DCT 变换,A_dct 为得到的 DCT 系数矩阵
A1 = idct2(A_dct); %二维逆 DCT 变换
A1 = uint8(A1);
figure, imshow(A1) %重建图像
- 一般来说,选取的 DCT 系数越大,水印嵌入对图像的影响就越小。为减少水印嵌入对图像的影响,从 DCT 系数矩阵中选取幅值较大的系数进行水印嵌入。
思路:可先将所有 DCT 系数变为一维行向量,然后按照幅值进行降序排序(sort 函数),选取排列靠前的 DCT 系数作为水印的具体嵌入位置。
- 长度为 k 的伪随机序列
w 1 , w 2 , ⋯ , w k w_{1}, w_{2}, \cdots, w_{k} w1,w2,⋯,wk作为无意义水印通过式 ( 3 ) (3) (3)嵌入原始图像,其中, c i c_i ci 为选取的 DCT 系数, c i ′ c'_i ci′ 为经过水印调整后的系数, α \alpha α 为嵌入强度。
c i ′ = c i ( 1 + α w i ) , 1 ≤ i ≤ k (3) c_{i}^{\prime}=c_{i}\left(1+\alpha w_{i}\right), \quad 1 \leq i \leq k \tag3 ci′=ci(1+αwi),1≤i≤k(3)
伪随机数序列类似于随机数序列,但它可以通过设置初始状态,来保证每次得到的随机数是相同的:
randn('seed', 0); %选定伪随机序列发生器“seed”和初始状态 0
K = randn(1, 1000); %产生长度为 1000 的伪随机数序列 K
- 在水印提取时,首先得到嵌入水印的 k 个 DCT 系数,然后通过式 ( 4 ) (4) (4)完成水印的恢复:
w ^ i = c ^ i − c i α c i , 1 ≤ i ≤ k (4) \hat{w}_{i}=\frac{\hat{c}_{i}-c_{i}}{\alpha c_{i}}, \quad 1 \leq i \leq k\tag4 w^i=αcic^i−ci,1≤i≤k(4)
the c ^ i \hat{c}_i c^i will be approximations of the c i ′ c_{i}^{\prime} ci′.
- 使用式 ( 5 ) (5) (5)给出的相关系数表达式,对提取的水印与原始水印的相关性进行评价,相关系数 γ γ γ 在 0 到 1 之间,其值越大,表示两者间的相关性越好,水印的损失也就越小。通过比较 γ γ γ 与预设定的阈值 T T T 可以判断一幅图像是否存在水印,详见教材 P397 式 ( 8.73 ) (8.73) (8.73)。
γ = ∑ i = 1 k ( w ^ i − w ^ ‾ ) ( w i − w ˉ ) ∑ i = 1 k ( w ^ i − w ^ ‾ ) 2 ∑ i = 1 k ( w i − w ˉ ) 2 , 1 ≤ i ≤ k (5) \gamma=\frac{\sum_{i=1}^{k}\left(\hat{w}_{i}-\overline{\hat{w}}\right)\left(w_{i}-\bar{w}\right)}{\sqrt{\sum_{i=1}^{k}\left(\hat{w}_{i}-\overline{\hat{w}}\right)^{2} \sum_{i=1}^{k}\left(w_{i}-\bar{w}\right)^{2}}}, \quad 1 \leq i \leq k\tag5 γ=∑i=1k(w^i−w^)2∑i=1k(wi−wˉ)2∑i=1k(w^i−w^)(wi−wˉ),1≤i≤k(5)
若图像遭到恶意攻击,水印信息会受到损坏,提取水印与原始水印的相关系数也会下降,而下降越小的水印算法其对各种攻击的鲁棒性就越强。