1.组合

题目链接

1. 过程图：先从集合中取一个数，再依次从剩余数中取k-1个数。

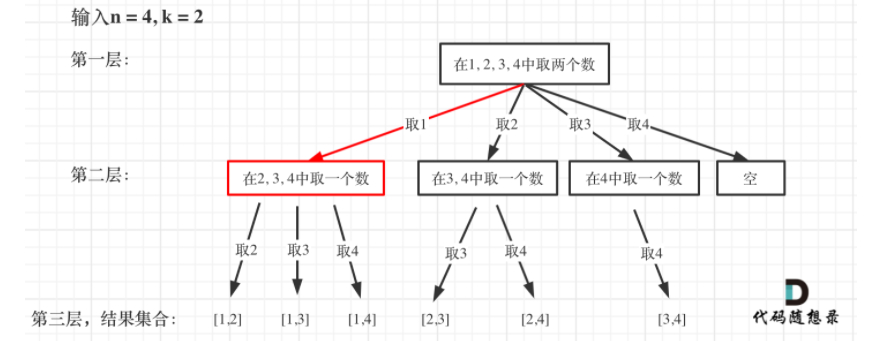
2. 思路：回溯算法。使用回溯三部曲进行解题：

• 递归函数的返回值以及参数：n，k，startIndex(记录每次循环集合从哪里开始遍历的位置)，其中startIndex 就是防止出现重复的组合。比如从1开始了循环，则使用startindex=2，让startindex作为下次循环的开始。

还有全局变量：一个是用来存放一个符合条件的结果path，一个用来存放所有符合条件的结果集合result。

• 回溯函数终止条件：path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合，在图中path存的就是根节点到叶子节点的路径

• 单层搜索的过程：for循环用来横向遍历，递归的过程是纵向遍历。

（1）for循环每次从startIndex开始遍历，然后用path保存取到的节点i。

（2）递归函数不断调用自己往深处遍历，总会遇到叶子节点，遇到了叶子节点就要返回。

（3）递归函数下面部分就是回溯的操作了，撤销本次处理的结果。

最终结果代码：

class Solution {
    // 存放单个结果path， 存放所有结果res
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        combineHelper(n, k, 1);
        return res;
    }
    
    // startindex就是循环开始位置
    private void combineHelper(int n, int k, int startindex) {
        // 终止条件 
        if (path.size() == k){
            res.add(new ArrayList<>(path));
            return;
        }
        // 单层逻辑
        for (int i = startindex; i <= n ; i++ ){
            path.add(i);
            combineHelper(n, k, i + 1);
            path.removeLast();
        }
    }
}

3. 剪枝优化：

（1）假设n = 4，k = 4，就四个数，还求四个数的组合，那必然只有一个组合，从2开始for循环再找其他数没有意义。所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置，在循环中i就是循环的起始位置。也就是说for循环的开始位置到结束位置一共的元素个数<k时，就不需要判断了。

（2）过程：

• 已经选择的元素个数：path.size();

• 还需要的元素个数为: k - path.size();

• 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历。也就是说 n - (k - path.size()) + 1是最晚的起始位置，如果超过了这个位置找元素，path的元素个数不可能到达k个。这里面+1是闭区间的意思。

最终优化后的代码：

List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {

    combineHelper(n, k, 1);
    return res;
}

private void combineHelper(int n, int k, int startindex) {

    if (path.size() == k){
        res.add(new ArrayList<>(path));
        return;
    }
    for (int i = startindex; i <= n - (k - path.size()) + 1; i++ ){
        path.add(i);
        combineHelper(n, k, i + 1);
        path.removeLast();
    }
}

2.组合总和III

题目链接

1. 过程图：和上一题组合类似，仍然是先取某个值，然后再从其他数中k-1个进行组合。

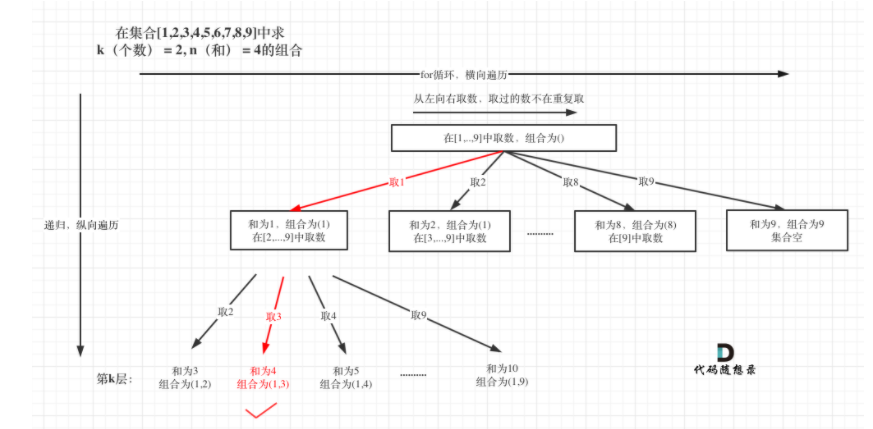
2. 思路：回溯三部曲。

• 确定递归函数参数：题目中的n和k，sum（已经收集的元素的总和也就是path里元素的总和），startIndex为下一层for循环搜索的起始位置。

• 确定终止条件：path.size() 和 k相等且sum=n

• 单层搜索过程： path收集每次选取的元素，sum来统计path里元素的总和。别忘了回溯。

3.代码：

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backTracking(n, k, 1, 0);
        return result;
    }
    
    // targetSum就是n， sum是和
    private void backTracking(int targetSum, int k, int startIndex, int sum) {
        // 减枝
        if (sum > targetSum) {
            return;
        }

        if (path.size() == k) {
            if (sum == targetSum) result.add(new ArrayList<>(path));
            return;
        }

        // 减枝 9 - (k - path.size()) + 1
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
            path.add(i);
            sum += i;
            backTracking(targetSum, k, i + 1, sum);
            //回溯
            path.removeLast();
            //回溯
            sum -= i;
        }
    }
}