目录
前言
算法原理
算法思想
数学模型
(1)种群初始化
(2)领导者位置更新
(3)跟随者位置更新
代码实现
算法流程图
算法步骤
伪代码
SSA伪代码
MSSA伪代码
面向全局搜索的自适应领导者樽海鞘群算法
1.1 改进领导者位置更新公式
1.2 引入领导者-跟随者自适应调整策略
基于混沌映射的自适应樽海鞘群算法
1.1 混沌映射
1.2 自适应权重变化
1.3 追随者机制变化
1.4伪代码
集成随机惯性权重和差分变异操作的樽海鞘群算法
1.1 PSO算法随机惯性权重的引入
1.2 集成DE算法的变异操作
基于疯狂自适应的樽海鞘群算法
1.1 Tent映射的种群初始化
1.2 疯狂算子
1.3自适应惯性权重
基于混合策略改进的樽海鞘群算法
(1)加权重心学习策略
(2)自适应惯性权重
(3)逐维随机差分变异
(4)改进后的算法步骤
基于自适应惯性权重的樽海鞘群算法
(1)惯性权重策略
(2)种群成功率策略
(3)差分变异策略
(4)算法步骤
算法拓展
改进的樽海鞘群算法
(1) 对领导者和追随者的改进
(2) 与其他优化算法相结合
1.引言
2.改进樽海鞘群算法
结合密度峰值聚类和改进樽海鞘群算法的遥感图像分割
1.1 基于超像素密度峰值聚类的图像分割
1.2 基于改进樽海鞘群的密度峰值聚类模型求解
1.3 实验结果与分析
代码实现
MATLAB
前言
樽海鞘是一种海洋无脊椎动物,身体呈桶状且几乎完全透明,以水中浮游植物为食,通过吸入和喷出海水完成在水中移动。在深海中,樽海鞘以一种链式的群行为进行移动和觅食,这种“奇特”的群行为引起了研究者的兴趣。樽海鞘的链式群行为,通常个体首尾相接,形成一条“链”,依次跟随进行移动。在樽海鞘链中,分为领导者和追随者,领导者朝着食物移动并且指导着紧随其后的追随者的移动,追随者的移动按照严格的“等级”制度,只受前一个樽海鞘影响。这样的运动模式使樽海鞘链有很强的全局探索和局部开发能力。
樽海鞘群算法( salp swarm algorithm,SSA)是Seyedali Mirjalili等于2017年提出的一种新型智能优化算法[1]。 该算法模拟了樽海鞘链的群体行为,是一种较新颖的群智能优化算法。每次迭代中,领导者指导追随者,以一种链式行为,向食物移动。移动过程中,领导者进行全局探索,而追随者则充分进行局部探索,大大减少了陷入局部最优的情况。
算法原理
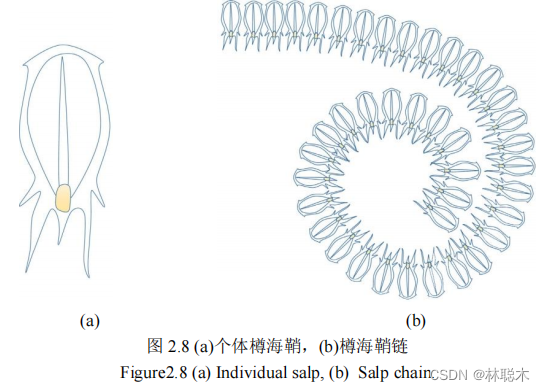
算法思想


牛顿运动定律通常用于更新追随者的位置为,
为了能够直观地观察 SSA 算法在寻优过程中的移动规律,图 2.9 给出了仿真实验。
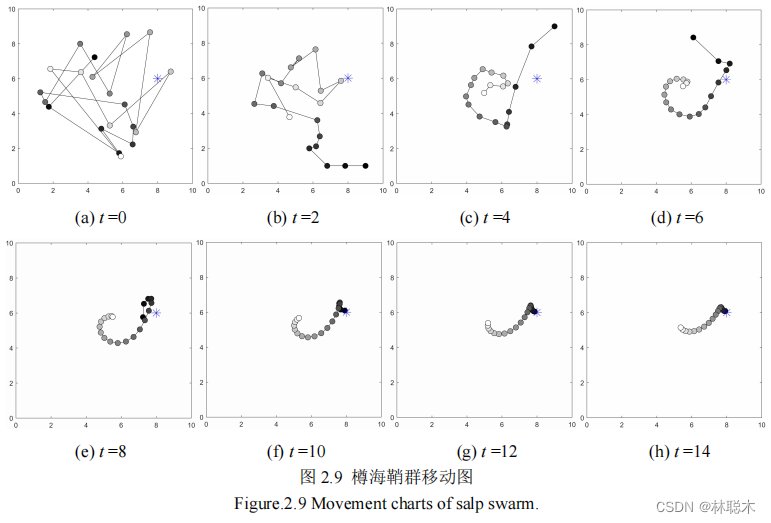
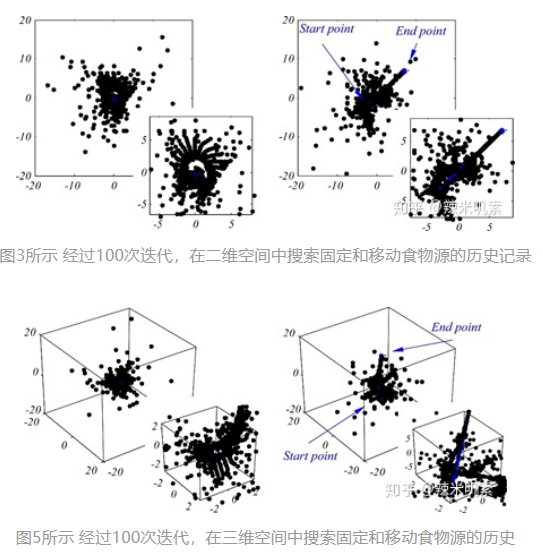
图3和图5显示了经过100次迭代后,在二维和三维空间中,salps在固定和流动食物源附近的位置历史。在固定食物源周围的搜索点表明,樽海鞘能有效地在搜索空间内移动。该模型的点分布合理,表明该模型能够对固定食物源周围的空间进行探索和开发。此外,图3和图5表明,所提出的数学模型要求在樽海鞘链中的樽海鞘追赶移动的食物源。搜索点在起始点附近的分布大于结束点。这是由于控制勘探和开发的c1参数造成的。这些发现证明,樽海鞘链运动模型能够探索和利用固定和流动食物源周围的空间。
数学模型
樽海鞘群算法(salp swarm algorithm,SSA)是Seyedali Mirjalili等于2017年提出的一种新型智能优化算法。每次迭代中,领导者指导追随者,以一种链式行为,向食物移动。移动过程中,领导者进行全局探索,而追随者则充分进行局部探索,大大减少了陷入局部最优的情况。樽海鞘群算法中有两类个体, 分别是领导者和跟随者。
为了建立樽海鞘链的数学模型,种群首先分为两组:领导者和追随者。领导者是位于食物链前端的樽海鞘,而其余樽海鞘则被视为追随者。正如这些樽海鞘的名字所暗示的,领袖引导种群,追随者互相跟随(直接或间接的领袖)。与其他基于群体的技术类似,在n维搜索空间中定义樽海鞘的位置,其中n是给定问题的变量数。 因此,所有樽海鞘的位置都存储在称为x的二维矩阵中。 还假定在搜索空间中有一个称为F的食物源作为种群的目标。
对应关系
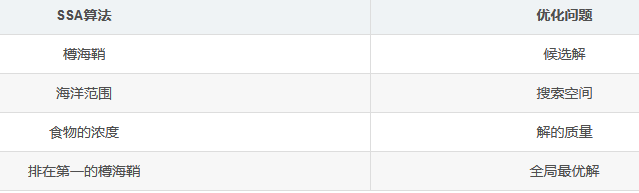
(1)种群初始化

(2)领导者位置更新
在樽海鞘链移动和觅食过程中,领导者的位置更新表示为:
式( 2) 表明,领导者的位置更新仅与食物的位置有关。 c1是优化算法中的收敛因子,起到平衡全局探索和局部开发的作用,是 SSA 中最重要的控制参数。c1的表达式为:

其中, l表示当前迭代次数,L表示最大迭代次数。可以发现,c1是樽海鞘群算法中最重要的参数,负责平衡开发和勘探。收敛因子是一个 2-0 的递减函数。控制参数c2、c3是[0,1]的随机数,用来增强 的随机性,提高链群的全局搜索和个体多样性。
(3)跟随者位置更新
在樽海鞘链移动和觅食的过程中,追随者通过前后个体间的彼此影响,呈链状依次前进。它们的位移符合牛顿运动定律,追随者的运动位移为:
考虑到在优化算法中,t 是迭代的,设迭代过程中t=1,并且 v0=0。那么式( 4) 可以表示为:

代码实现
###定义一个樽海鞘类
#樽海鞘个体继承于上次写的个体基类,并多了两个方法,分别是对于不同樽海鞘的位置更新方法。
class Salp(baseIndividual):
def update_head(self, best_position : np.ndarray, c1 : float):
# c2 = random.random() # 同一随机数
c2 = np.random.random_sample(self.x_dim) # 每一维度不同随机数
c3 = random.random()
second_part = c1 * (self.across * c2 + self.l_bound)
if c3 < 0.5:
self.position = best_position - second_part
else:
self.position = best_position + second_part
def update_other(self, prev):
self.position += prev.position
self.position /= 2
###定义樽海鞘群算法
class SalpSwarm(baseSIOA):
individual_class_build_up_func = Salp
def __init__(self, objective_func, salp_num, search_space, constraint_func = None):
'''
:param objective_func: 目标函数,参数为 x 向量 \n
:param salp_num: 樽海鞘个数 \n
:param search_space: x 在各维度的取值范围,shape = (2, x_dim) \n
:param constraint_func: 约束条件函数 bool 值函数\n
'''
super(SalpSwarm_test, self).__init__(objective_func, salp_num, search_space, constraint_func = constraint_func)
self.salp_swarm = self.individual_swarm
def c1_formula(self, t : int, T : int) -> float:
return 2 * math.exp(- (4 * t / T) ** 2)
def iteration(self, iter_num : int) -> IterationResult:
best_fitness_value = []
self.get_fitness()
best_salp_index = np.argmin(self.fitness)
best_fitness_value.append(self.fitness[best_salp_index])
best_position = self.salp_swarm[best_salp_index].position
# print(best_position, self.fitness[best_salp_index])
for t in tqdm(range(1, iter_num + 1)):
# for t in range(1, iter_num + 1):
c_1 = self.c1_formula(t, iter_num)
for i, single_salp in enumerate(self.salp_swarm):
if i == 0:
# 链头产生新解
single_salp.update_head(best_position, c_1)
else:
# 其他产生新解
single_salp.update_other(self.salp_swarm[i - 1])
if self.constraint_func:
self.constraint()
else:
self.bound_check()
self.get_fitness()
best_salp_index = np.argmin(self.fitness)
best_fitness_value.append(self.fitness[best_salp_index])
best_position = self.salp_swarm[best_salp_index].position.copy()
return IterationResult(
{
'best_position' : best_position,
'best_fitness' : self.fitness[best_salp_index],
'best_fitness_value_history' : best_fitness_value
}
)
###写测试函数
import numpy as np
from Algorithms.SSA import SalpSwarm
def cost(x : np.ndarray) -> float:
return (x[0]** 2 - 2) ** 2
if __name__ == '__main__':
search_space = np.array([
[0],
[2]
])
solver = SalpSwarm(cost, 30, search_space)
solution_dict = solver.iteration(100)
solution = solution_dict.best_position
print('solution = ', solution[0])算法流程图
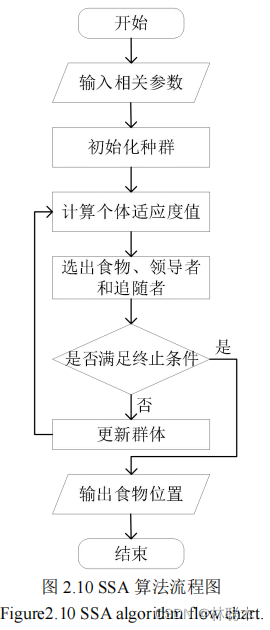
- 1)初始化种群。根据搜索空间每一维的上界与下界,利用式(1)初始化一个规模为N ×D 的樽海鞘 群。
- 2)计算初始适应度。计算 N 个樽海鞘的适应度值。
- 3)选定食物。由于实际定位时我们不知道目标(即食物)的位置,因此,将樽海鞘群按照适应度值进行排序,排在首位的适应度最优的樽海鞘的位置设为当前食物位置。
- 4)选定领导者与追随者。选定食物位置后,群体中剩余N −1 个樽海鞘,按照樽海鞘群体的排序,将排在前一半的樽海鞘视为领导者,其余樽海鞘视为追随者。
- 5)位置更新。首先根据式(2)更新领导者的位置,再根据式(6)更新追随者的位置。
- 6)计算适应度。计算更新后的群体的适应度。将更新后的每个樽海鞘个体的适应度值与当前食物的适应度值进行比较,若更新后樽海鞘的适应度值优于食物,则以适应度值更优的樽海鞘位置作为新的食物的位置。
- 7)重复步骤4)-步骤6),直到达到一定迭代次数或适应度值达到终止门限,满足终止条件后,输出当前的食物位置作为目标的估计位置。
算法步骤
伪代码
SSA伪代码
在SSA群模型中,跟随者跟随领头者。领头的樽海鞘也向食物来源移动。因此,如果食物来源被全局最优的替代,樽海鞘食物链就会自动向它移动。但问题是优化问题的全局最优是未知的。在这种情况下,我们假设到目前为止得到的最优解是全局最优解,并假设其为樽海鞘链所追逐的食物来源。
SSA算法的伪代码如下图所示。从图中可以看出,SSA算法通过初始化多个随机位置的樽海鞘来近似全局最优。然后计算每个樽海鞘的适合度,找到适合度最好的樽海鞘,并将最佳的樽海鞘的位置分配给变量F,作为樽海鞘链要追赶的源食物。同时利用公式(3.2)更新系数c1。对于每一个维度,使用Eq.(3.1)更新领先跳跃体的位置,使用Eq.(3.4)更新跟随跳跃体的位置。如果其中任何一个跃出了搜索空间,它将被带回边界。除初始化外,以上所有步骤都将迭代执行,直到满足end标准。

需要注意的是,在优化过程中,食物来源会被更新,因为樽海鞘链很有可能通过探索和开发它周围的空间找到更好的解决方案。
前文中的群模拟表明,所模拟的樽海鞘链能够追赶移动的食物源。因此,樽海鞘链有可能朝着在迭代过程中改变的全局最优方向移动。如何提出樽海鞘链模型和SSA算法在解决优化问题是有效的,下面列出一些批注:
- SSA算法将目前得到的最优解保存下来,并将其分配给食物源变量,这样即使整个种群恶化也不会丢失。
- SSA算法只更新了领导者樽海鞘相对于食物源的位置,食物源是迄今为止获得的最佳解,因此领导者总是探索和利用食物源周围的空间。
- SSA算法更新跟随的樽海鞘之间的相对位置,使他们逐渐向领先的樽海鞘移动。
- 追随者的渐进运动防止SSA算法容易陷入局部最优。
- 参数c1在迭代过程中自适应地减少,因此SSA算法首先探索全局搜索空间,然后深入探索局部最优。
- SSA算法只有一个主控制参数(c1)。
- SSA算法简单,易于实现。
这些说明使得SSA算法在理论上和潜在上能够解决搜索空间未知的单目标优化问题。
SSA的自适应机制使得该算法可以避免局部解,最终找到优化过程中得到的最优解的准确估计。因此,它既适用于单峰问题,又适用于多峰问题。上述优点可能使SSA能够超过最近的算法(MFO、GWO、ABC等)。然而,根据NFL定理,这并不能保证所有的优化问题都是如此。
注意,SSA算法的计算复杂度为O(t(d*n + Cof*n)),其中t为迭代次数,d为变量数(维数),n为解数,Cof为目标函数的代价。
MSSA伪代码
多目标问题的解决方案是一组称为帕累托最优集的解决方案。SSA算法能够驱动salps向食物来源靠近,并在迭代过程中对其进行更新。但是,该算法不能解决多目标问题,主要有以下两个原因:
- SSA只保存一个解决方案作为最佳解决方案,因此它不能存储多个解决方案作为一个多目标问题的最佳解决方案。
- SSA在每次迭代中都用迄今为止得到的最优解更新食物源,但对于多目标问题没有单一的最优解。
通过给SSA算法配备一个食物来源库来解决第一个问题。该存储库维护了到目前为止优化过程中获得的最优解,非常类似于多目标粒子群优化(MOPSO)中的存档[78]。存储库有一个最大大小来存储数量有限的最优解决方案。在优化过程中,使用Pareto优势操作符将每个樽海鞘与所有存储库原方案进行比较。
- 如果一个樽海鞘在存储库中占优,则必须交换它们(把樽海鞘放入存储库,原方案拿出)。如果一个樽海鞘在存储库中优于一组解决方案,那么应该将这一组解决方案全部从存储库中删除,并把该樽海鞘应该添加到存储库中。
- 如果至少有一个存储库中的原方案比该樽海鞘更优,那么该樽海鞘应被丢弃,不加入存储库。
- 如果与所有存储库居民相比,该樽海鞘与之互不占优,那么该樽海鞘即是最优解,则必须将其添加到存储库中。
这些规则可以保证存储库得到的始终都是目前为止算法所获得的最优解决方案。但是,有一种特殊情况,即存储库已满,与存储库原方案相比,该樽海鞘也不占优,此时本应该将该樽海鞘加入存储库,但是存储库满了。当然,最简单的方法是随机删除归档中的一个解决方案,并将其替换为这个樽海鞘。
更明智的方法是在存储库中删除一个类似的非主导解决方案:从存档中删除的最佳候选方案是在一个种群稠密的区域。这种方法改进了在迭代过程中存储库中方案的分布。
为求邻域有人口的非支配解,需要计算邻域有一定最大距离的解的个数。这个距离的定义是:
Max和min分别是存储每个目标函数的最大值和最小值的两个向量。每个段中有一个解决方案的存储库是最好的情况。(我认为是目前存储库里的max和min,因此存储库只有一个d。)在根据相邻解决方案的数量为每个存储库驻留分配级别之后,将使用轮盘赌来选择其中一个删除。一个解决方案的相邻解决方案的数量越多(级别数越大),从存储库中删除它的可能性就越大。图7展示了该存储库更新机制的示例。注意邻域应该为所有的解定义,但是在这个图中只研究了4个非支配解
如上所述,介绍了存储库的更新机制后,使用SSA解决多目标问题的第二个问题是食物来源的选择,因为在多目标搜索空间中有不止一个最佳解。同样,可以从存储库中随机选择食物来源。然而,更合适的方法是从一组最优解决方案中选择最不拥挤的区域。这可以使用存储库维护操作符中使用的相同的排序过程和轮盘赌轮选择来完成。主要的区别是选择最优解决方案的概率。在存储库维护删除中,等级越高(邻里拥挤)的解决方案越容易被选择。相比之下,对于存储库中的最优解决方案而言,人口越少(较低的等级数),被选为食物来源的可能性就越大。(这样就能更多地开发未探索的区域,加强全局搜索能力,如果一直检索密集区域容易陷入局部最优,选择稀疏的区域作为食物能够减少陷入局部最优的可能性。)例如在图7中,中间没有相邻方案的最优解被选择为食物来源的概率最大。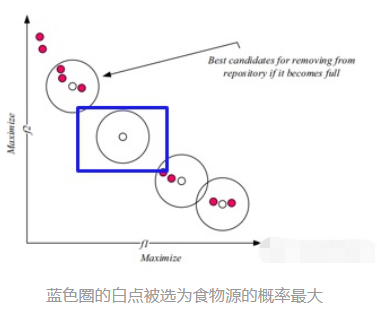
下图显示,MSSA算法首先根据变量的上界和下界对樽海鞘种群进行初始化。然后,该算法计算出每个樽海鞘的适应值,并通过pareto比较找出最优的樽海鞘。如果存储库未满,则将该樽海鞘添加到存档中。如果存储库已满,则运行存储库维护以删除邻域拥挤的解决方案。在这一步,解决方案首先按照拥挤度排名,然后选择使用轮盘赌轮。在删除足够数量的存储库方案之后,可以最优樽海鞘添加到存储库中。更新存储库后,从存储库中最不拥挤的解决方案中选择食物来源。与存档维护类似,这是通过对解决方案进行排序并使用轮盘赌轮来完成的。下一步是使用Eq.(3.2)更新c1,并使用Eq.(3.1)或(3.4)更新领导者/跟随者樽海鞘的位置。如果在更新位置的过程中,一个樽海鞘超出了边界,它将被带回到边界上。最后,重复上述除初始化外的所有步骤,直到满足结束条件。
为了了解MSSA算法的有效性,以下是一些注释:
- 到目前为止获得的最优解存储在一个存储库中,因此即使在一次迭代中整个种群恶化,最优解也不会丢失。
- 每次存储库维护时,都会丢弃最拥挤邻居的解决方案,这将提高其他最优解决方案在所有目标中的覆盖率。
- 从相邻解个数最少的解列表中选择一个食物源,这将引导搜索获得的帕累托最优前沿的不那么拥挤的区域,并提高找到的解的覆盖范围。(加强全局寻优能力)
- MSSA继承了SSA的操作符,因为它使用了类似的种群划分(领导者和跟随者)和位置更新过程。
- MSSA算法只有两个主要控制参数(c1和存储库大小)。
- MSSA算法简单,易于实现。
这些评论表明MSSA算法在逻辑上能够找到在所有目标中具有高分布的精确帕累托最优解。注意MSSA算法的计算复杂度为O(t(d*n + Cof*n + M*n2)),其中M表示目标数量,t表示迭代次数,d表示变量数量(维数),n表示解的数量,Cof表示目标函数的代价。
面向全局搜索的自适应领导者樽海鞘群算法
为了进一步改善基本樽海鞘群算法容易陷入局部最优,寻优精度有时不高,求解结果不太稳定的不足,提出了一种面向全局搜索的自适应领导者樽海鞘群算法。在领导者位置更新公式中引入上一代樽海鞘群位置,增强了全局搜索的充分性,有效避免算法陷入局部极值。然后在领导者位置更新公式中加入惯性权重,并在全局和局部搜索的选择上引入领导者-跟随者数量自适应调整策略,使算法在迭代前期领导者数目较多且受全局最优解影响较大,能以较大的全局搜索步幅快速收敛到全局最优区域;而在迭代后期领导者步幅较小且跟随者数量较多,可以在最优解附近深度挖掘,提高算法的收敛精度。
1.1 改进领导者位置更新公式
1.1.1 引入上一代樽海鞘领导者位置
在基本樽海鞘群算法中, 樽海鞘领导者从迭代 开始就奔向全局最优值, 导致全局搜索不充分, 容 易陷入局部极值区域,造成算法有时收敛精度较低。 本文在领导者位置更新公式中引入上一代樽海鞘领 导者位置, 使得领导者在位置更新阶段既受上一代 楢海鞘领导者位置的影响, 同时又受上一代全局最 优解的影响, 有效地避免了基本算法易陷入局部极 值的问题, 提高了算法的寻优精度。改进后的樽海 鞘领导者位置更新公式为:
 一代的位置,樽海鞘领导者能够更有效地进行全局搜索, 增强算法 跳出局部极值的能力。
一代的位置,樽海鞘领导者能够更有效地进行全局搜索, 增强算法 跳出局部极值的能力。
1.1.2 引入惯性权重
本文还在领导者位置更新公式中引入动态惯性权重,随迭代次数自适应递减的惯性权重 w 表示了樽海鞘领导者受全局最优解影响程度的变化。在迭代前期,领导者受全局最优解影响较大,有较大的全局搜索步幅,能够更快速地找到全局最优区域。而在迭代后期,大部分樽海鞘都已达到较优值,领导者受全局最优解影响变小, 领导者可以在最优解附 近深度挖掘, 提高了算法的收敛精度。本文中惯性 权重的计算公式为:
1.2 引入领导者-跟随者自适应调整策略
在基本 SSA 算法中,樽海鞘领导者和跟随者的数目始终是各占种群中个体数的一半,这就使得在迭代前期,执行全局搜索的领导者比例过低,跟随者比例过高,领导者无法有效地进行全局搜索,全局搜索不充分,容易陷入局部最优;而在迭代后期,执行局部搜索的跟随者比例过低,局部搜索不够充分,容易造成寻优精度不高。针对此问题,本文引领导者-跟随者自适应调整策略,樽海鞘领导者的数目随迭代次数的增加自适应减少,跟随者数目自适应增加,在算法前期能够保持很强的全局搜索能力,同时兼顾局部搜索,而在算法运行后期,局部搜索逐渐增强,同时也兼顾全局搜索,从整体上提高了算法的收敛精度。改进后的领导者-跟随者数量计算公式为: 其中, t 是当前迭代次数, Max_iter 是最大迭 代次数。 b 为控制领导者-跟随者数量的比例系数, 避 免迭代前期的樽海鞘领导者或迭代后期的樽海鞘跟 随者比例过高, 全局和局部搜索失衡降低寻优性能, 易陷入局部极值的现象, 经大量实验测试, 本文取 值为0.75 。分析式 (8) 可知, r 的值随着算法迭代次数的增加呈非线性递减趋势, 于是领导者数量逐 渐减少, 跟随者数量逐渐增加, 在迭代后期, 更多的 樽海鞘跟随者在全局最优值附近深度挖掘。k 为扰 动偏离因子, 结合 rand 函数对递减的 r 值进行扰动, 经大量实验反复测试, k 等于0.2 时, 寻优效果最佳。
其中, t 是当前迭代次数, Max_iter 是最大迭 代次数。 b 为控制领导者-跟随者数量的比例系数, 避 免迭代前期的樽海鞘领导者或迭代后期的樽海鞘跟 随者比例过高, 全局和局部搜索失衡降低寻优性能, 易陷入局部极值的现象, 经大量实验测试, 本文取 值为0.75 。分析式 (8) 可知, r 的值随着算法迭代次数的增加呈非线性递减趋势, 于是领导者数量逐 渐减少, 跟随者数量逐渐增加, 在迭代后期, 更多的 樽海鞘跟随者在全局最优值附近深度挖掘。k 为扰 动偏离因子, 结合 rand 函数对递减的 r 值进行扰动, 经大量实验反复测试, k 等于0.2 时, 寻优效果最佳。
基于混沌映射的自适应樽海鞘群算法
针对樽海鞘群算法收敛速度慢、易陷入局部最优等问题,提出了一种基于混沌映射的自适应樽海鞘群算法。在种群初始化阶段引入混沌映射来增强种群的多样性,提高算法的收敛速度;改进领导者的更新方式,同时加入自适应权重,提高算法的探索和开发能力;改进追随者的位置更新方式,减少追随者的盲目性。
1.1 混沌映射
研究表明, 种群初始化作为群能算法的重要环 节, 初始化的位置的好坏可以直接影响算法的收敛 速度和解质量 , 例如, 均匀分布比随机分布解 空间的覆盖率更全, 更容易得到好的初始解。基本 樽海鞘群算法采用随机种群初始化操作, 无法覆盖 整个解空间。混池序列在一定范围内具有遍历性、 随机性及规律性的特点与随机搜索相比, 混池序列 能以更高的概率对搜索空间进行彻底搜索, 可使算 法跳出局部最优, 保持群体的多样性。
基于以上分析, 为了更大几率的得到好的初始 解位置, 加快种群的收玫速度, 本文采用具有较好遍 历均匀性和更快迭代速度的 Tent 混池映射方法, 提 高初始解的覆盖空间, 计算方法如式 (8) 所示。
1.2 自适应权重变化
在基本樽海鞘群算法中, 从领导者的位置更新方 式我们可以看出,领导者的位置更新主要受到食物源 和参数 c1 的影响, c1 值越大时有利于算法的探索能 力, c1 值越小时, 有利于算法的开发能力, 同时领导者 的位置移动还受到缩放因子c2 的影响, c2 为均匀分 布的随机数, 这样的缩放因子使得领导者的移动具有 很大的斍目性, 且 c2 的取值多为无效取值。针对上 述问题, 本文提出了一种新的领导者位置更新方式, 在食物源的位置添加自适应权重, 算法前期权重较 大, 让算法有足够强的探索能力, 随着迭代次数的增 加,权重自适应减小,用于增强算法的局部开发能力, 在算法的中后期, 权重开始增大, 使领导者具备跳出 局部最优的能力, 具体数学描述如式 (10) 所示。
1.3 追随者机制变化
在基本樽海鞘群算法中, 追随者根据式(7) 进 行位置更新, 从式中可以看出,第i 只个体根据第 i− 1 只个体进行位置移动, 而没有考虑上一个体适应 度的好与坏, 即追随者的位置移动具有一定的斍目 性,追随者 i 的位置移动只与个体i−1 有关, 缺乏与 其他个体进行信息交流的能力, 这种移动方式极易 导致算法陷入局部最优。针对上述缺点, 本文提出 了一种新的追随者移动方式, 具体数学描述如式 (12) 所示。
领导者c2 的适应 度, 则在适应度较大的个体位置上添加权重因子, 用 来降低较差位置个体的影响, 进而提升了较优个体 的权重; 否则, 个体i 只在自已周围波动。这种移动 方式, 可以大大的降低斍目追随性,增强了种群间的 信息交流,同时还能保留追随者的自身信息,保证种 群的多样性。
1.4伪代码
本文通过添加混沌映射和自适应权重,同时改变领导者和追随者的位置更新方式,得到了改进的樽海鞘群算法(CASSA) ,平衡了领导者的探索和开发能力,降低了追随者盲目性,更好的保留了个体信息,同时保证种群的多样性,CASSA的具体算法伪代码如下图所示。

集成随机惯性权重和差分变异操作的樽海鞘群算法
为了提高樽海鞘群算法(Salp Swarm Algorithm,SSA)的收敛速度、计算精度和全局优化能力,在分析总结粒子群优化(Particle Swarm Optimization,PSO)和差分进化(Differential Evolution,DE)算法相关研究成果后,提出了一种集成PSO算法随机惯性权重和DE算法差分变异操作的改进SSA算法——iSSA。首先,将PSO算法的随机惯性权重引入SSA算法的追随者位置更新公式中,用于增强和平衡SSA算法的勘探与开发能力;其次,用DE算法的变异操作替代SSA算法的领导者位置更新操作,以提高SSA算法的收敛速度和计算精度。
1.1 PSO算法随机惯性权重的引入

在 PSO 算法中, 粒子速度更新直接决定着粒子位置更 新。惯性权重是 PSO 算法粒子速度更新公式中的重要参数, 它体现了上一代粒子对当前粒子速度更新的影响力, 用于平 衡 PSO 算法的勘探与开发 。尽管迄今为止已有大量学者 提出了各种 PSO 算法惯性权重控制策略, 但文献 [15] 的研究 表明, 在总计 18 种 PSO 算法惯性权重控制策略中, 除了随机 惯性权重以外, 常数项惯性权重优于其他所有的惯性权重控 制策略。
常数项惯性权重需要繁琐的算法参数调校, 因此本文将PSO 算法的随机惯性权重引入 SSA 算法追随者位置更新操 作中, 从而得到追随者位置更新公式:
其中, Random(0,1) 表示均匀分布于 (0,1) 内的随机数, 故 w 的取值范围为(0.5,1) 。显然, 此处引入的随机惯性权重没有 改变 SSA 算法的时间复杂度。
1.2 集成DE算法的变异操作
根据 SSA 算法的式(1), 在领导者位置更新操作中, 参与 者是食物源且没有追随者, 缺乏樽海鞘之间的协作和信息共 享, 容易导致 SSA算法过早收敛于较差的局部最优解。
变异操作是 DE 算法的重要组成部分, 它一般通过 3 个 不同的个体来为种群内每一个个体生成一个新个体, 通过比 例因子可以调节算法开发和勘探之间的平衡 。目前 DE 算法研究中最典型的变异操作有 5 种, 其中与 SSA 算法的式 (1)一样包含最优解且形式最简单的变异操作一般简称为:“DE/best/1” DE 。
综上所述, 本文提出用DE 算法的上述变异操作来替代 SSA 算法领导者的位置更新操作, 从而得到如式 (6) 所示的 领导者位置更新操作:
基于疯狂自适应的樽海鞘群算法
针对樽海鞘群算法求解精度不高和收敛速度慢等缺点,提出一种基于疯狂自适应的樽海鞘群算法. 引入Tent混沌序列生成初始种群,以增加初始个体的多样性;在食物源位置上引入疯狂算子,增强种群的多样性;在追随者位置更新公式中引入自适应惯性权重,使算法的全局搜索和局部搜索能力得到更好的平衡。
1.1 Tent映射的种群初始化
樽海鞘群体的初始化对SSA算法的收敛速度与寻优精度至关重要. 在樽海鞘群初始时,由于没有任何先验知识可使用,基本上大部分群智能算法的初始位置均采用随机生成.
混沌序列具有随机性、遍历性和规律性等特点,通过其产生的樽海鞘群体有较好的多样性. 基本思路是通过映射关系在[0,1]区间产生混沌序列,将混沌序列转化到个体的搜索空间. 产生混沌序列的模型有许多,Tent映射比Logistic映射能够生成更好的均匀序列 . 本文采用Tent映射生成的混沌序列初始化樽海鞘群算法群体,其数学表达式为:
1.2 疯狂算子
在樽海鞘群算法中,种群的食物源位置有重要作用,引导着群体向最优解移动,但若食物源位置陷入局部最优,则容易导致群体出现搜索停止,即群体内多样性缺失. 樽海鞘在移动的过程中,食物源不可能一直保持其位置不变,它们可能会突然变换位置,以此来增加种群的意外行为. 本文采用“疯狂”因素来描述这种行为,其核心思想是通过疯狂变量对其进行建模. 为了减少SSA算法出现早熟的收敛现象,本文提出在樽海鞘群算法领导者的位置更新公式中引入一个疯狂算子,确保樽海鞘在预先设定的疯狂概率下,对食物源位置产生一定扰动,以此维持个体的多样性. 新的领导者更新公式如下:
在求解测试函数优化问题中,搜索范围变化较大. 为了使樽海鞘群算法前期搜索具有更好的全局性和随机性,本文选取多个领导者进行更新,但领导者太多,算法随机性较强,会导致算法稳定性降低,因此,为了权衡算法的随机性和稳定性,选取一半的樽海鞘个体作为领导者.
1.3自适应惯性权重
惯性权重ω体现的是追随者继承前一个樽海鞘位置的能力. 文献[14]将惯性权重ω 引入PSO算法中,分析指出:当惯性权重值较大时,有助于提升探索能力;当惯性权重较小时,有助于具体开发能力. 由式(5)追随者位置更新公式可知,第i只樽海鞘位置会根据第i和第i − 1只樽海鞘位置进行更新,对先前个体依懒性较强. 若追随者的位置是局部最优解,则会容易陷入局部最优,出现停滞. 为了更好地权衡樽海鞘群算法的探索能力与开发能力,引入线性递减的惯性权重,它决定了先前个体对当前个体的影响程度. 新的追随者位置公式为:
基于混合策略改进的樽海鞘群算法
(1)加权重心学习策略
本文提出了加权重心,根据个体的优劣状况使用不同的权重来计算重心,可以在不忽略较差个体的同时向更多优秀个体学习,合理利用了种群的信息,同时避免了只向最优个体学习陷入早熟。
修改后的公式可以在向最优解逐渐学习的同时没有过多丢失种群多样性。 w w w用来调节个体在搜索过程中对自身位置的依赖,搜索前期较低的 w w w可以降低个体对自身的依赖,从而增大了搜索的范围,算法的全局搜索能力得到增强。搜索后期 w w w逐渐向1靠拢,不影响算法寻优。
(2)自适应惯性权重
自适应惯性权重在很多群体智能优化算法中被使用,搜索前期权重较大,可以增强全局搜索能力,搜索后期自适应权重较小,可以增强局部寻优能力。使用的自适应惯性权重公式为
(3)逐维随机差分变异
使用随机差分变异进行逐维变异,通过该变异得到一个新的个体的维度,具体公式为

在种群位置更新完成后,使用逐维随机差分变异对个体的每个维度进行变异,某一维度进行变异后对其进行评价,如果优秀,则保留变异后的解,如果变异后评价结果变差,则舍弃较差的维度信息,减少了各个维度间的干扰,同时增大了搜索的范围。由于变异操作具有一定的盲目性,将所有个体都进行逐维随机差分变异势必会导致算法的搜索效率下降和计算量大幅的增加,所以仅挑选种群中最优秀和最差个体进行变异,对最优个体变异可以提高搜索效率,对最差个体变异可以提高搜索范围,跳出局部最优解。
(4)改进后的算法步骤
为了算法在迭代的前期能够有较强的全局搜索能力,选取种群中前一半的个体作为领导者,增多领导者可以增强算法的随机性。算法具体步骤如下:
a)初始种群和参数。初始化种群个体数量 N,最大迭代次数T,随机初始化种群位置。
b)计算种群每个个体的适应度,最优的个体作为食物位置。
c)根据位置更新公式更新个体位置。前一半个体为领导者使用式(4)进行更新,后一半个体为追随者使用式(6)进行更新。
d)对更新完的个体选择最优和最差个体,对其通过式(7)进行逐维随机差分变异,将更新的维度与其余维度组成新的个体,比较变异前后个体适应度值的变化,如果好则保留。
e)找出最优个体适应度值更新食物位置。
f)判断是否满足迭代次数要求或精度要求,若是转步骤g),否则返回步骤c)。
g)输出最优个体的适应度值。
基于自适应惯性权重的樽海鞘群算法
为平衡SSA的全局和局部搜索能力,首先在追随者位置更新时引入基于非线性递减函数的惯性权重因子;然后引入种群成功率作为反馈参数对惯性权重因子自适应调整。此外,为防止陷入局部最优,对非最优个体进行差分变异,增加种群的多样性。
(1)惯性权重策略
本文引入基于非线性递减函数的惯性权重因子来评价樽海鞘链中第i−1只追随者对第 i i i只追随者的影响程度,改进的追随者位置更新公式如下:
(2)种群成功率策略
由公式(2)可以看出, ω(t)按照关于迭代次数 t的非线性函数递减,因为不监测个体位置、适应度值等情况的变化,忽略了种群所处的实际环境,不能完全体现实际的优化搜索过程,因此,其本质上并不是自适应的。本文在此基础上引入种群成功率,并以此为反馈参数对公式(1)进一步改进,使得 ω(t)根据种群状态进行自适应调整。
以最小化问题为例,樽海鞘链的个体 i 在第 t 次迭代中的成功值 S(i,t)定义为
(3)差分变异策略
对非最优的个体进行变异,可以增加其在下次迭代中成为最优个体的可能性,提高算法跳出局部最优的能力。本文引入差分进化中个体变异的思想,根据变异算子DE/best/1对非最优个体进行变异:

(4)算法步骤
为了在随机性与稳定性之间取得权衡,本文选取一半的樽海鞘个体作为领导者。AIWSSA步骤如Algorithm 1所示。

算法拓展
改进的樽海鞘群算法
(1) 对领导者和追随者的改进
(2) 与其他优化算法相结合
1.引言
2.改进樽海鞘群算法
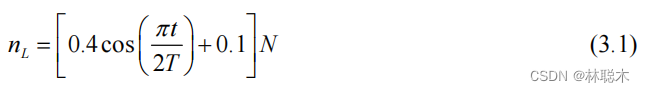
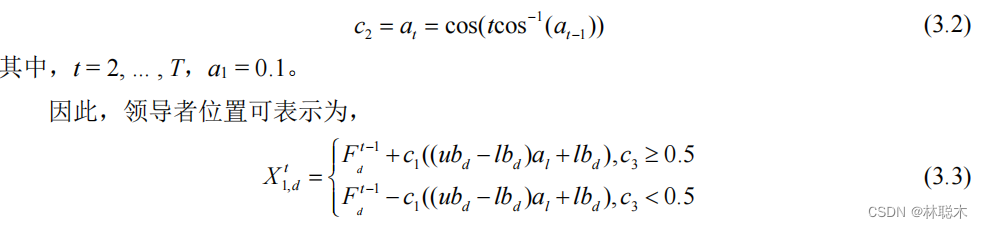








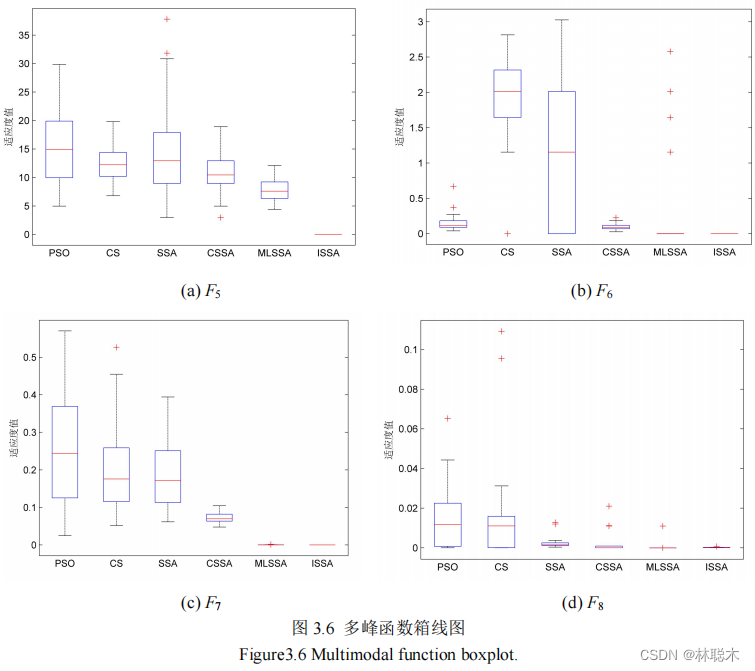
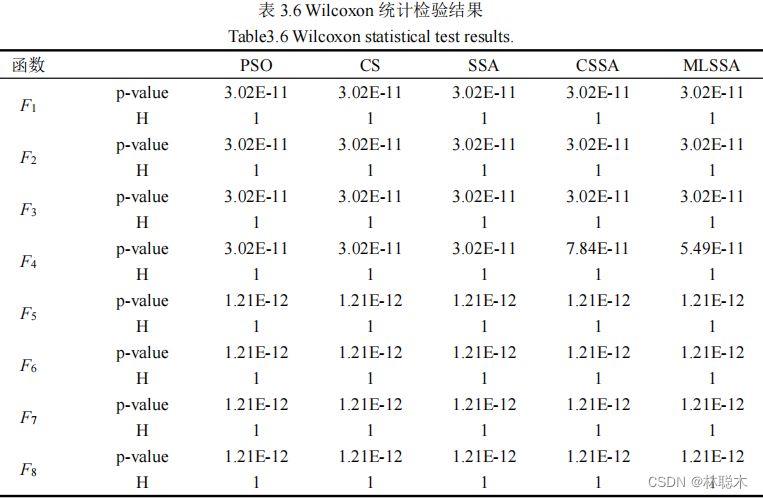
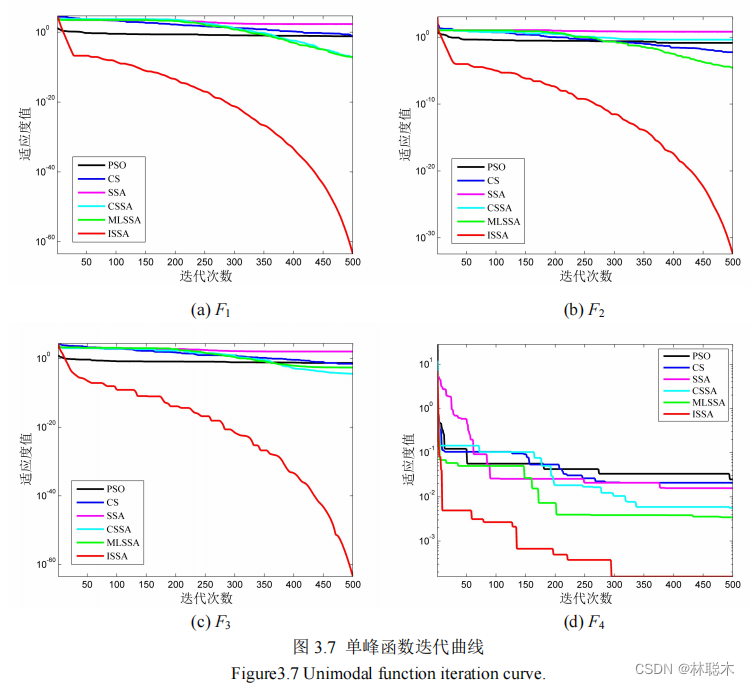
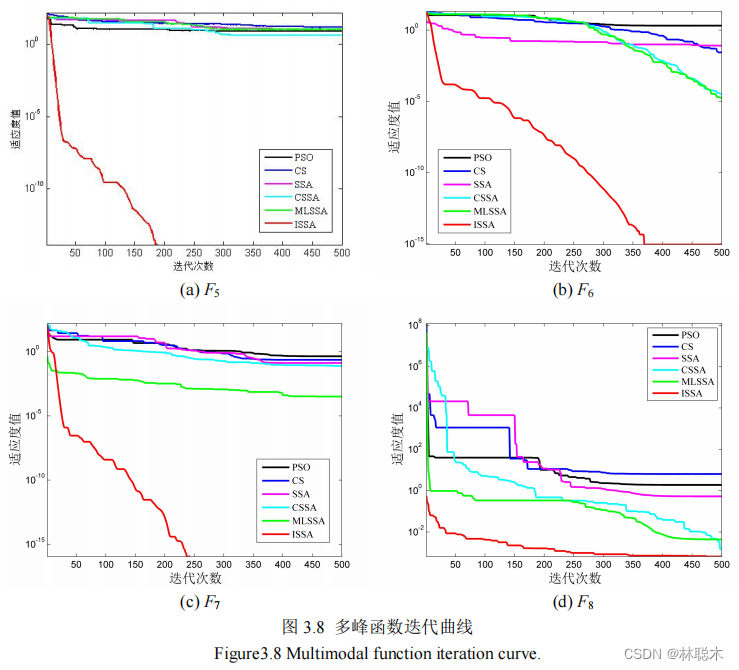
结合密度峰值聚类和改进樽海鞘群算法的遥感图像分割
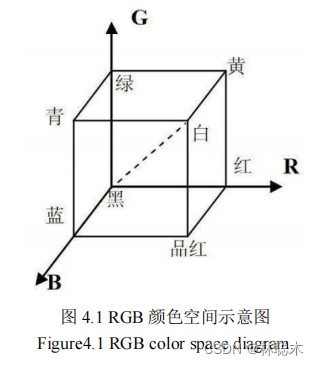
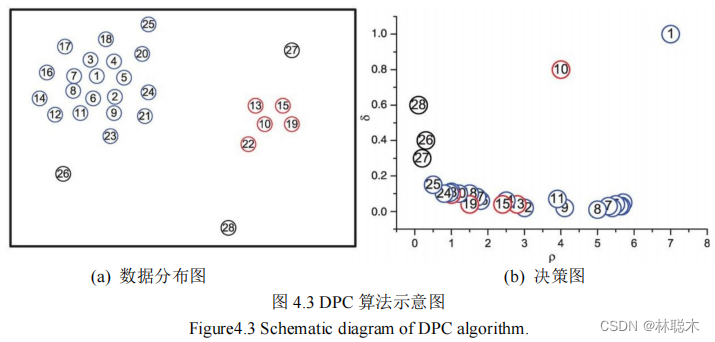
1.1 基于超像素密度峰值聚类的图像分割
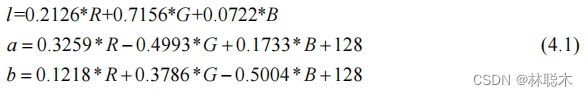


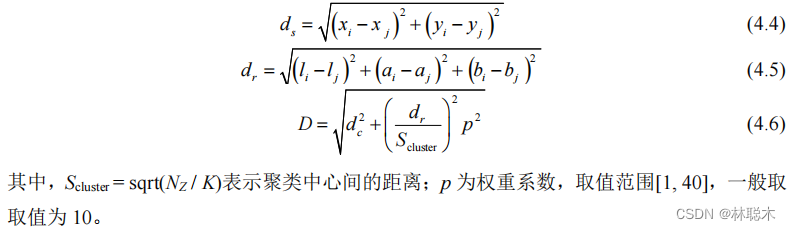



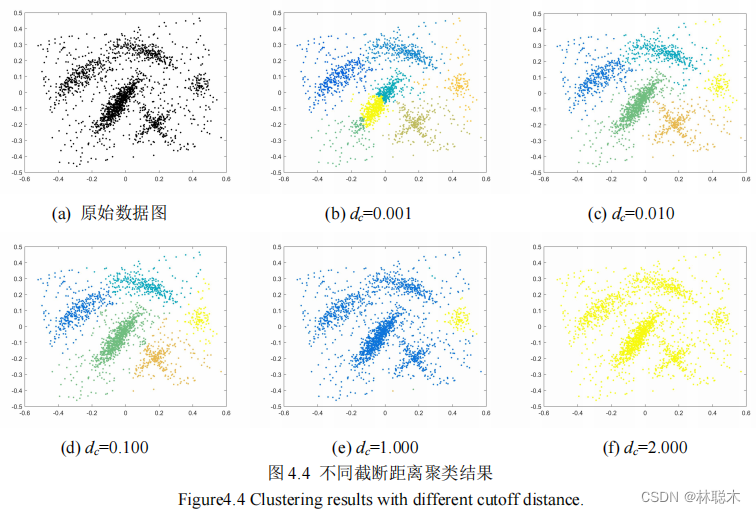
1.2 基于改进樽海鞘群的密度峰值聚类模型求解


1.3 实验结果与分析
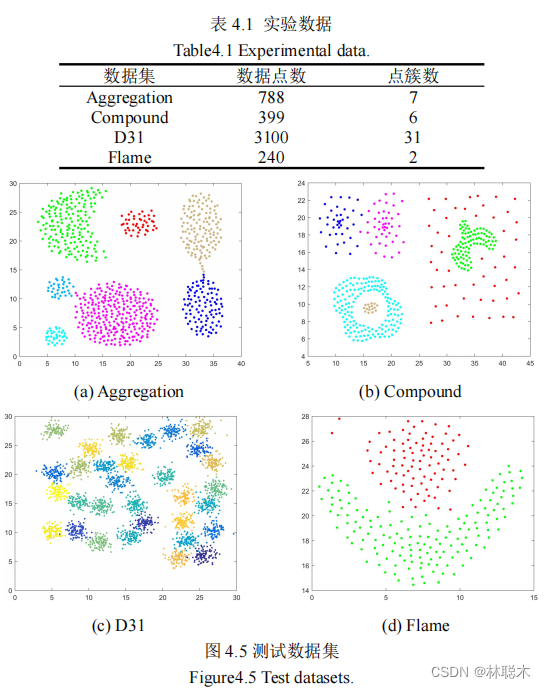


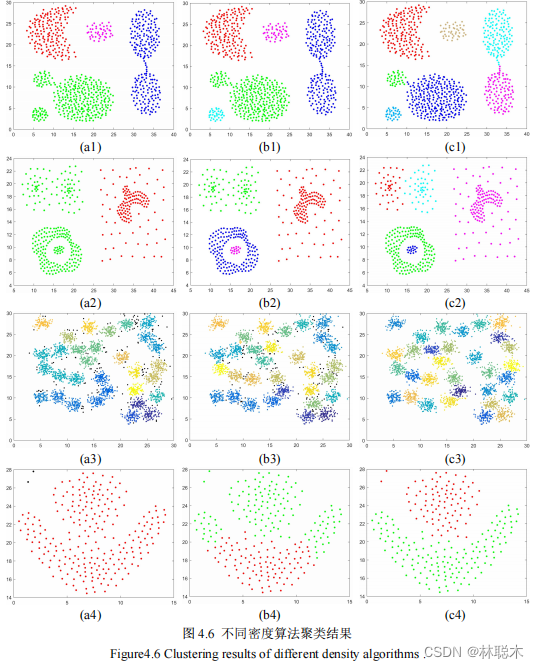
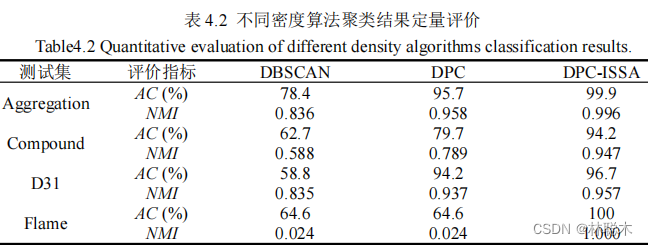








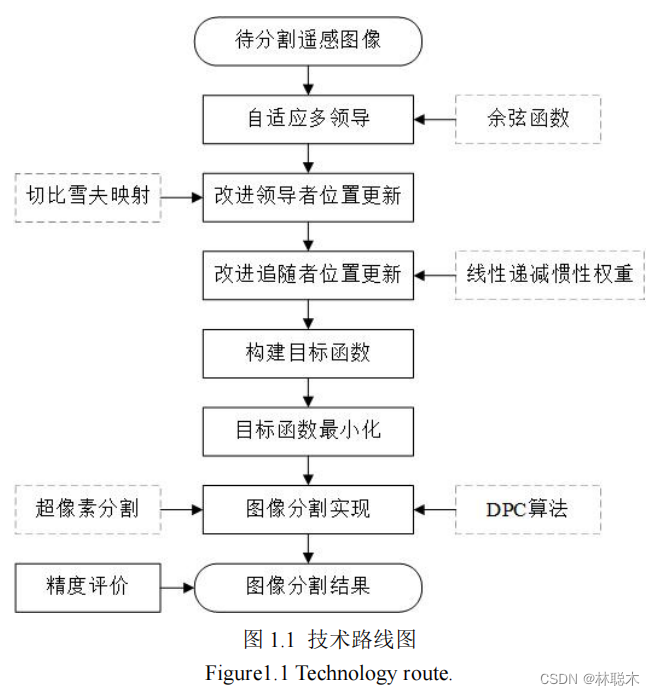
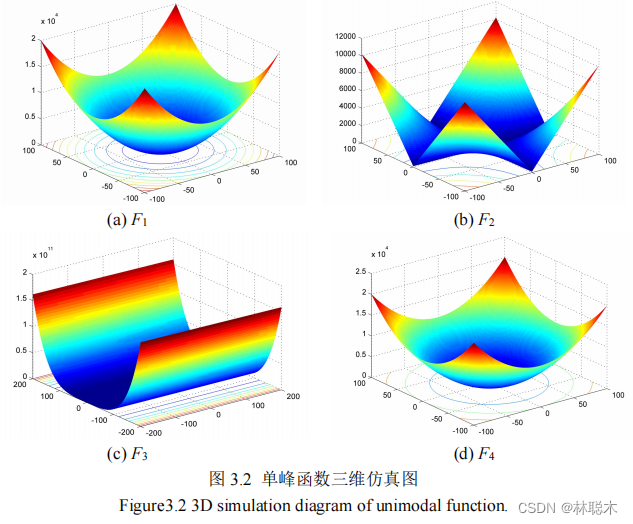
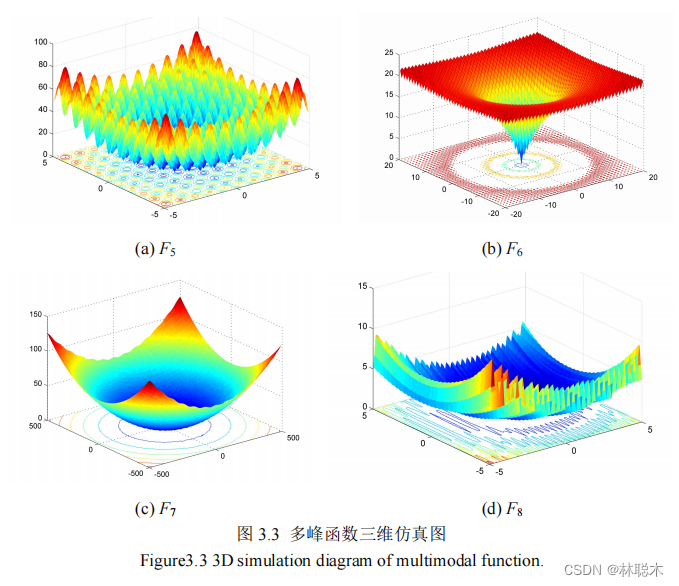
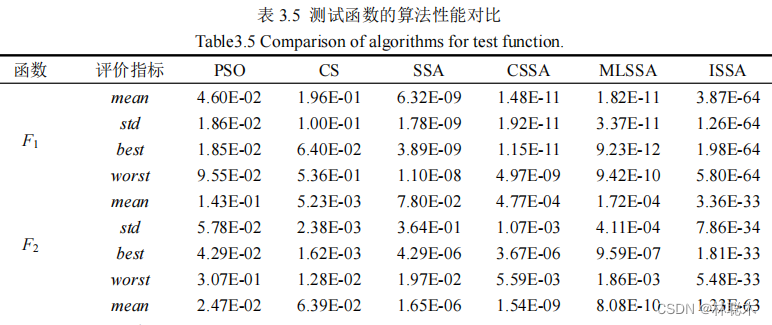
(3) GCE。基于实际分割图与标准分割图之间区域的重叠程度实现分割质量评价,即,



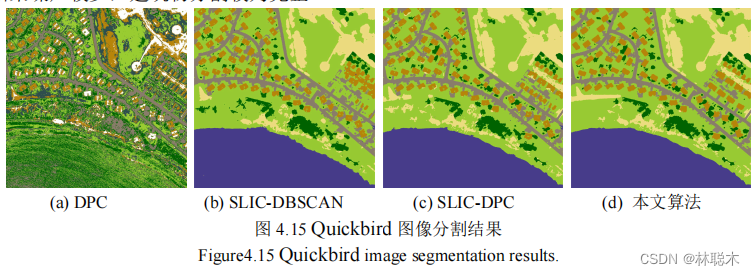
图 4.13(a)中地物主要包括耕地、草地、灌木、道路和建筑物五类。从图 4.14 实验结果
代码实现
MATLAB
initialization.m
function X=initialization(SearchAgents_no,dim,ub,lb)
Boundary_no= size(ub,2); % numnber of boundaries
% If the boundaries of all variables are equal and user enter a signle
% number for both ub and lb
if Boundary_no==1
ub_new=ones(1,dim)*ub;
lb_new=ones(1,dim)*lb;
else
ub_new=ub;
lb_new=lb;
end
% If each variable has a different lb and ub
for i=1:dim
ub_i=ub_new(i);
lb_i=lb_new(i);
X(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
end
X=X;
func_plot.m
function func_plot(func_name)
[lb,ub,dim,fobj]=Get_Functions_details(func_name);
switch func_name
case 'F1'
x=-100:2:100; y=x; %[-100,100]
case 'F2'
x=-100:2:100; y=x; %[-10,10]
case 'F3'
x=-100:2:100; y=x; %[-100,100]
case 'F4'
x=-100:2:100; y=x; %[-100,100]
case 'F5'
x=-200:2:200; y=x; %[-5,5]
case 'F6'
x=-100:2:100; y=x; %[-100,100]
case 'F7'
x=-1:0.03:1; y=x %[-1,1]
case 'F8'
x=-500:10:500;y=x; %[-500,500]
case 'F9'
x=-5:0.1:5; y=x; %[-5,5]
case 'F10'
x=-20:0.5:20; y=x;%[-500,500]
case 'F11'
x=-500:10:500; y=x;%[-0.5,0.5]
case 'F12'
x=-10:0.1:10; y=x;%[-pi,pi]
case 'F13'
x=-5:0.08:5; y=x;%[-3,1]
case 'F14'
x=-100:2:100; y=x;%[-100,100]
case 'F15'
x=-5:0.1:5; y=x;%[-5,5]
case 'F16'
x=-1:0.01:1; y=x;%[-5,5]
case 'F17'
x=-5:0.1:5; y=x;%[-5,5]
case 'F18'
x=-5:0.06:5; y=x;%[-5,5]
case 'F19'
x=-5:0.1:5; y=x;%[-5,5]
case 'F20'
x=-5:0.1:5; y=x;%[-5,5]
case 'F21'
x=-5:0.1:5; y=x;%[-5,5]
case 'F22'
x=-5:0.1:5; y=x;%[-5,5]
case 'F23'
x=-5:0.1:5; y=x;%[-5,5]
end
L=length(x);
f=[];
for i=1:L
for j=1:L
if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
f(i,j)=fobj([x(i),y(j)]);
end
if strcmp(func_name,'F15')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
if strcmp(func_name,'F19')==1
f(i,j)=fobj([x(i),y(j),0]);
end
if strcmp(func_name,'F20')==1
f(i,j)=fobj([x(i),y(j),0,0,0,0]);
end
if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
end
end
surfc(x,y,f,'LineStyle','none');
end
Get_Functions_details.m
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=30;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=10;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=10;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=10;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=10;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=10;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=10;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=10;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=10;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=10;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=10;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=10;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=10;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
% F5
function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
% F6
function o = F6(x)
o=sum(abs((x+.5)).^2);
end
% F7
function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
% F8
function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end
% F10
function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
% F11
function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end
% F12
function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
endinitialization.m
function Positions=initialization(SearchAgents_no,dim,ub,lb)
Boundary_no= size(ub,1); % numnber of boundaries
% If the boundaries of all variables are equal and user enter a signle
% number for both ub and lb
if Boundary_no==1
Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;
end
% If each variable has a different lb and ub
if Boundary_no>1
for i=1:dim
ub_i=ub(i);
lb_i=lb(i);
Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
end
endSSA.m
function [FoodFitness,FoodPosition,Convergence_curve]=SSA(N,Max_iter,lb,ub,dim,fobj)
if size(ub,1)==1
ub=ones(dim,1)*ub;
lb=ones(dim,1)*lb;
end
Convergence_curve = zeros(1,Max_iter);
%Initialize the positions of salps
SalpPositions=initialization(N,dim,ub,lb);
FoodPosition=zeros(1,dim);
FoodFitness=inf;
%calculate the fitness of initial salps
for i=1:size(SalpPositions,1)
SalpFitness(1,i)=fobj(SalpPositions(i,:));
end
[sorted_salps_fitness,sorted_indexes]=sort(SalpFitness);
for newindex=1:N
Sorted_salps(newindex,:)=SalpPositions(sorted_indexes(newindex),:);
end
FoodPosition=Sorted_salps(1,:);
FoodFitness=sorted_salps_fitness(1);
%Main loop
l=2; % start from the second iteration since the first iteration was dedicated to calculating the fitness of salps
while l<Max_iter+1
c1 = 2*exp(-(4*l/Max_iter)^2); % Eq. (3.2) in the paper
for i=1:size(SalpPositions,1)
SalpPositions= SalpPositions';
if i<=N/2
for j=1:1:dim
c2=rand();
c3=rand();
%%%%%%%%%%%%% % Eq. (3.1) in the paper %%%%%%%%%%%%%%
if c3<0.5
SalpPositions(j,i)=FoodPosition(j)+c1*((ub(j)-lb(j))*c2+lb(j));
else
SalpPositions(j,i)=FoodPosition(j)-c1*((ub(j)-lb(j))*c2+lb(j));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
end
elseif i>N/2 && i<N+1
point1=SalpPositions(:,i-1);
point2=SalpPositions(:,i);
SalpPositions(:,i)=(point2+point1)/2; % % Eq. (3.4) in the paper
end
SalpPositions= SalpPositions';
end
for i=1:size(SalpPositions,1)
Tp=SalpPositions(i,:)>ub';Tm=SalpPositions(i,:)<lb';SalpPositions(i,:)=(SalpPositions(i,:).*(~(Tp+Tm)))+ub'.*Tp+lb'.*Tm;
SalpFitness(1,i)=fobj(SalpPositions(i,:));
if SalpFitness(1,i)<FoodFitness
FoodPosition=SalpPositions(i,:);
FoodFitness=SalpFitness(1,i);
end
end
Convergence_curve(l)=FoodFitness;
l = l + 1;
end
main.m
clc
clear
close all
SearchAgents_no=30; % Number of search agents
Function_name='F1'; % Name of the test function that can be from F1 to F23 (
Max_iteration=1000; % Maximum numbef of iterations
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,SSA_cg_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
figure('Position',[300 300 660 290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
%Draw objective space
subplot(1,2,2);
semilogy(SSA_cg_curve,'Color','r')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
axis tight
grid on
box on
legend('SSA')
display(['The best solution obtained by SSA is ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by SSA is ', num2str(Best_score)]);