"明白成功,不一定赢在起跑线!"
位图反思
上篇呢,我们在遇到海量数据时,如果只是进行诸如,查找一个数在不在这样的简单逻辑情况,在使用数组这样的内存容器,无法存储这么多数据时,我们采用新的数据结构——"位图"。
那么位图有什么弊端嘛?

我们举一个例子,要在1,2,3,4,2^32-1,2^32-2,2^32-3中查看5在不在!是的数据很大,所以我们开位图结构要开足足2^32-1个比特位,用于直接定址映射。但是,你会发现,你就仅仅是在这不到10个数中,查找5,却开开辟了512MB空间用来标记。
因此,位图只适合以用于 "数据量范围集中" , 并且是整数! 你的位图结构不可能存储string类型的对象。
那如果此时给你一个全部用户的名单,你要在用户名单中找出进入黑名单的用户,并将它剔除,你如何快速找到该名字并判断?? 位图结构肯定不行! 因为姓名 不是整数。
----前言
一、布隆过滤器简介
布隆过滤器(Bloom Filter)是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的 优点是空间效率和查询时间都比一般的算法要好的多,缺点是 有一定的误识别率和删除困难。 取自这里
看文字不好理解,我们直接上图。

"在"是准确,还是"不在"是准确?
字符串转换不像整数!整数就是一个一个的Key值。但是字符串转换后的整型,是有可能一样的!这和哈希冲突类似。
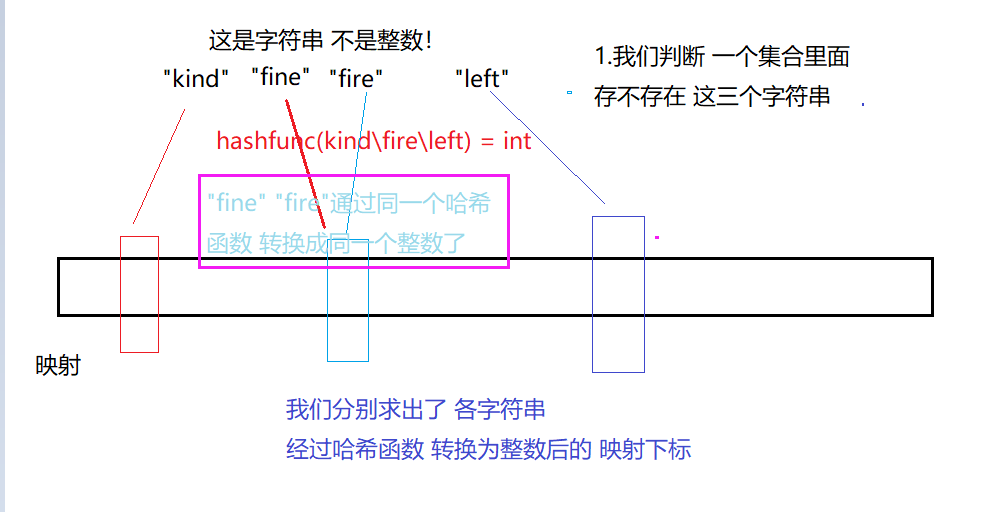
因此,布隆过滤器是存在误判的!
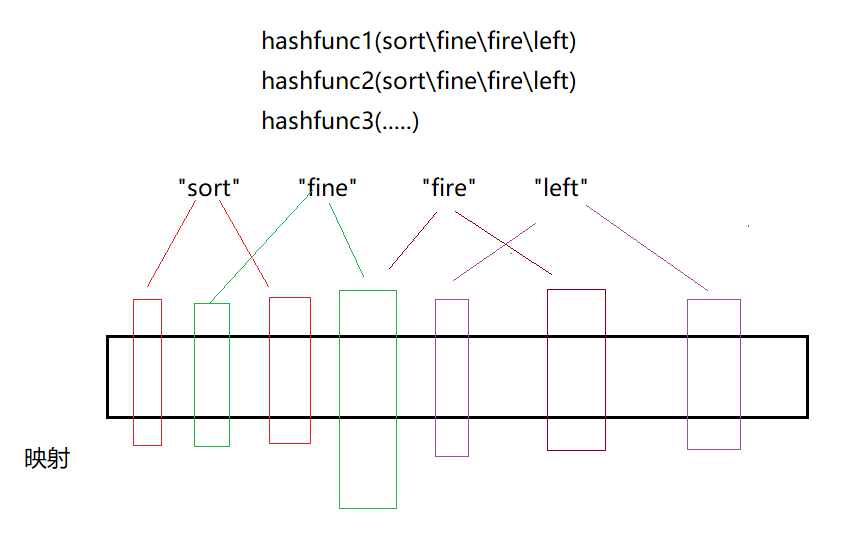
为了降低误判率!我们时常会多增添几个哈希函数,让一个字串映射多个位置。相应地,你较之前降低了误判的概率,但却让一个值映射多个位置,无疑增加了空间的消耗。当然,作何取舍是需要我们去权衡的。
布隆过滤器的价值在于:
"不在",是准确的!"在",是不准确(存在误判)。
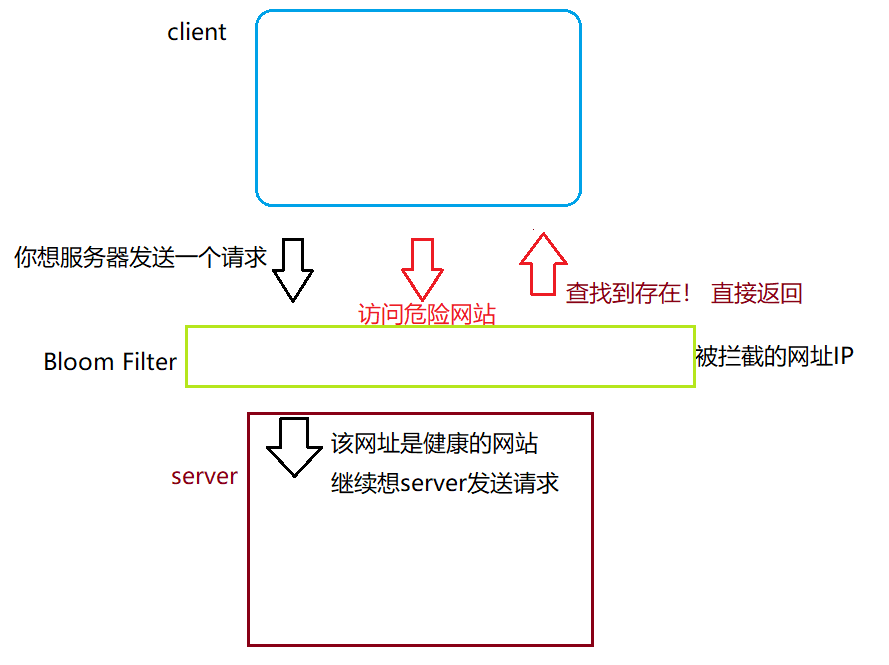
二、布隆过滤器实现
(1)布隆过滤器长度
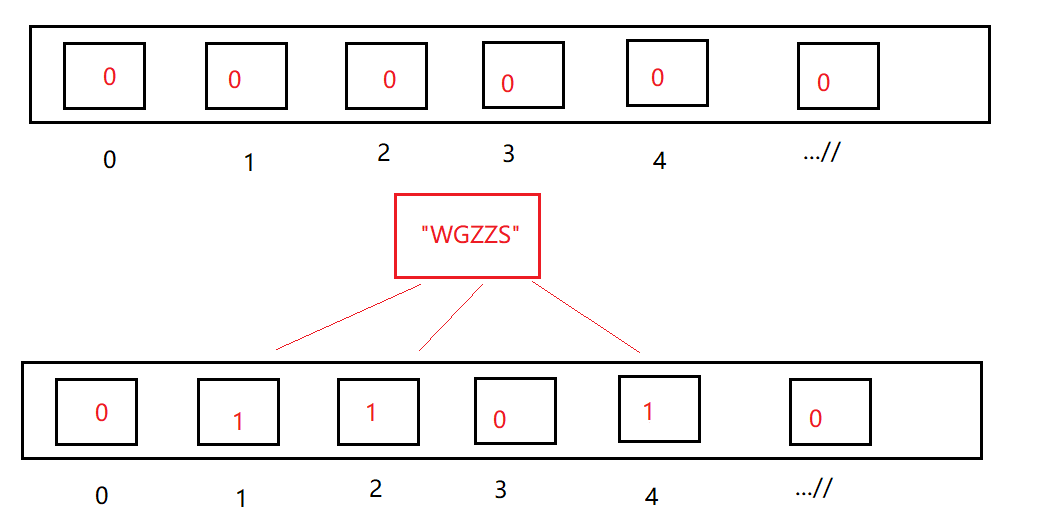
布隆过滤器的底层,其实就是位图结构。当然,与位图结构有去别的是,你不知道开辟多少个bit位。你使用一个哈希函数,那么表示一个数值在不在的就是1bit,如果你用两个哈希函数,那么表示一个数值在不在的就是2bit,如果你用三个哈希函数……这里有一个公式,可以计算出布隆过滤器开辟的空间大小 取自这里

(2)哈希函数选择
字符串转整数的函数特别多,这里就截取几个。 取自这里
//N表示 最多存储的个数
template<size_t N,
size_t X = 6,
class K = std::string,
class HashFunc1 = BKDRHash,
class HashFunc2 = APHash,
class HashFunc3 = DJBHash>
class bloomfilter
{
public:
void set(const K& key)
{
//计算 下标
size_t hash1 = HashFunc1()(key) % (N * X);
size_t hash2 = HashFunc2()(key) % (N * X);
size_t hash3 = HashFunc3()(key) % (N * X);
//设置进位图
_bloomfilter.set(hash1);
_bloomfilter.set(hash2);
_bloomfilter.set(hash3);
}
bool test(const K& key)
{
size_t hash1 = HashFunc1()(key) % (N * X);
//只有不在才是准确的
if (!_bloomfilter.test(hash1))
{
return false;
}
size_t hash2 = HashFunc2()(key) % (N * X);
if (!_bloomfilter.test(hash2))
{
return false;
}
size_t hash3 = HashFunc3()(key) % (N * X);
if (!_bloomfilter.test(hash3))
{
return false;
}
//说明该字符串各个位置 都映射了
//虽然 返回true 但可能存在误判
return true;
}
private:
std::bitset<N* X> _bloomfilter;
};(3)set\test
void set(const K& key)
{
//计算 下标
size_t hash1 = HashFunc1()(key) % (N * X);
size_t hash2 = HashFunc2()(key) % (N * X);
size_t hash3 = HashFunc3()(key) % (N * X);
//设置进位图
_bloomfilter.set(hash1);
_bloomfilter.set(hash2);
_bloomfilter.set(hash3);
}
bool test(const K& key)
{
size_t hash1 = HashFunc1()(key) % (N * X);
//只有不在才是准确的
if (!_bloomfilter.test(hash1))
{
return false;
}
size_t hash2 = HashFunc2()(key) % (N * X);
if (!_bloomfilter.test(hash2))
{
return false;
}
size_t hash3 = HashFunc3()(key) % (N * X);
if (!_bloomfilter.test(hash3))
{
return false;
}
//说明该字符串各个位置 都映射了
//虽然 返回true 但可能存在误判
return true;
}不解释。
(4)测试
分别产含有10000个字符串集的数组,其中的元素有相似的和非相似的。
void TestBloomFilter()
{
srand(time(0));
const size_t N = 10000;
bloomfilter<N> bf;
//1.相似字符集
std::vector<std::string> Array_Same;
std::string url = "www.baidu.com";
for (size_t i = 0; i < N; ++i)
{
Array_Same.push_back(url + std::to_string(i));
}
//设置
for (auto& e : Array_Same)
{
bf.set(e);
}
std::vector<std::string> Array_Differ;
for (size_t i = 0;i < N;++i)
{
Array_Differ.push_back(url + std::to_string(rand() + i));
}
//查找
size_t n2 = 0;
for (auto& str : Array_Differ)
{
if (bf.test(str))
{
++n2;
}
}
//第二个字符集 映射出来的位置 与 第一字串集 比较
std::cout << "相似字符 串误判率:" << (double)n2 / (double)N << std::endl;
std::vector<std::string> Array;
for (size_t i = 0; i < N; ++i)
{
std::string url = "qq.com";
url += std::to_string(i + rand());
Array.push_back(url);
}
n2 = 0;
for (auto& e : Array)
{
if (bf.test(e))
{
n2++;
}
}
std::cout << "不相似字符 串误判率:" << (double)n2 / (double)N << std::endl;
}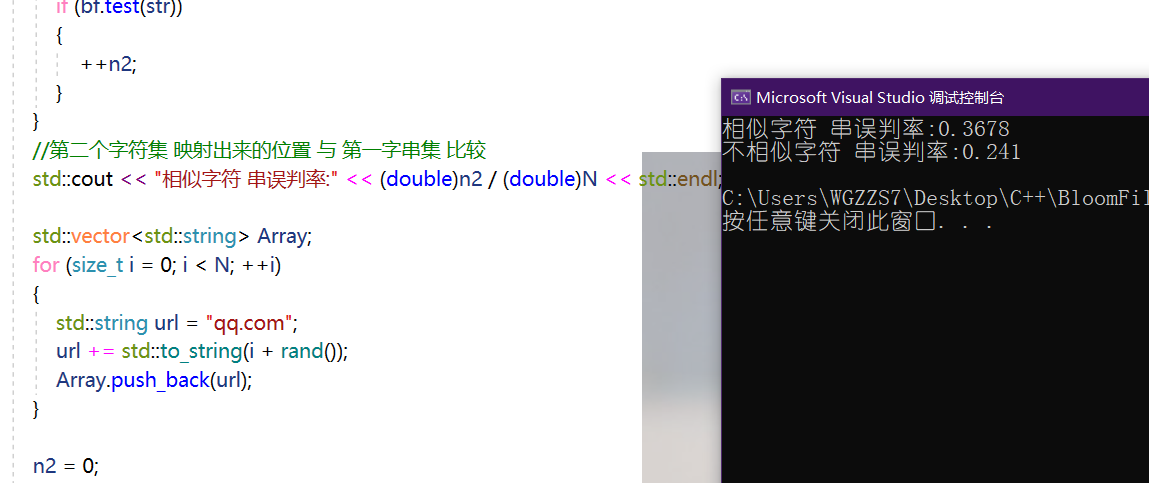
也进一步证明了,布隆过滤器的误差判断。
总结:
布隆过滤器最重要的是它是存在是准确的,还是不存在是准确的,这是面试经常问的。